MIMO雷达收发阵列互耦误差自校正方法与流程

本发明属于雷达技术领域，特别涉及雷达收发阵列互耦误差的校正方法，可用于MIMO雷达探测。

背景技术：

多输入多输出MIMO雷达作为一种新体制雷达，可以通过多个发射天线发射不同信号，多个接收天线同时接收回波并进行信号处理。理论研究表明，MIMO雷达在自由度、抗杂波、多目标检测与跟踪、角度分辨率等方面的性能相比传统雷达均有明显地改进。但以上优良性能的取得都是以精确已知的阵列流形为前提的，在实际的工程应用中，由于互耦误差的存在，实际的阵列流形会出现一定的偏差。阵列流形失配会严重恶化MIMO雷达方向图赋形的能力，波形分集带来的优势也将大打折扣。因此阵列互耦误差的校正具有重要的现实意义，也是实际工程应用中一个亟待解决的问题。

现有阵列误差校正分为有源和自校正两大类。考虑阵列互耦误差是时变的，基于回波数据的自校正方法不受场地环境等因素的限制，工作方式更灵活，具有更强的实用性。传统自校正方法基于相控阵体制，主要关注接收端误差特性，没有考虑发射端互耦误差问题，且往往基于大量独立同分布样本数据，而实际环境复杂多变，样本资源相对稀缺，因此传统自校正方法不能很好的发挥作用。

技术实现要素：

本发明的目的在于针对上述现有技术的不足，提出一种基于单快拍MIMO雷达回波数据的收发互耦误差校正方法，以解决传统方法无法在线实时校正发射端互耦误差及对样本需求大的问题。

为实现上述目的，本发明的技术方案如下：

(1)MIMO雷达发射正交信号，经某方位稀疏的杂波散射体反射后得到回波数据X，对该回波数据进行脉冲压缩得到数据矩阵Y；

(2)对数据矩阵Y进行取列操作，得到数据矩阵第m列的数据Y_m，根据接收阵列互耦自由度p_r截取数据Y_m的中间有效孔径数据，再利用空间平滑算法构造l×2_q维伪协方差矩阵R，其中q为划分的子阵个数，l为子阵阵元数；

(3)根据伪协方差矩阵R估计强杂波方位信息：

(3a)对伪协方差矩阵R进行奇异值分解，得到J个大奇异值及由大奇异值对应的奇异向量张成的信号子空间U_s和l-J个小奇异值及由小奇异对应的奇异向量张成的噪声子空间U_n，J为强杂波点的个数；

(3b)利用信号子空间U_s与噪声子空间U_n的正交性，计算强杂波方位估计值θ_j；

(4)利用步骤(2)得到的数据矩阵Y_m与步骤(3)估计的强杂波的方位估计值θ_j，构造代价函数并采用交替迭代的方法估计等效杂波散射系数β′_j与接收互耦误差矩阵C_r：

(4a)以最小化重构误差为准则，构建包含接收互耦误差的代价函数为：

其中a_r(θ_j)为θ_j方向的接收导向矢量，J为强杂波点的个数；

(4b)初始化交替迭代算法的参数，假设初始不存在互耦误差，即C_r＝I；

(4c)将C_r的估计值带入代价函数，用最小二乘法得到等效杂波散射系数β′_j的估计值；

(4d)将(4c)得到的等效杂波散射系数β′_j的估计值带入代价函数，得到接收互耦误差矩阵C_r的估计值；

(4e)重复步骤(4c)-(4d)，直至代价函数不再减小；

(5)利用步骤(4)估计的接收互耦矩阵C_r与步骤(3)的强杂波方位估计值θ_j求解发射互耦误差矩阵C_t；

(5a)用C_r的逆矩阵补偿回波数据矩阵Y，得到补偿后的回波矩阵：对Y′进行取行操作得到第n行的数据Y_n′；

(5b)结合步骤(3)估计的强杂波的方位值θ_j，以最小化重构误差为准则构建包含发射互耦误差的代价函数：

其中β″_j是估计发射互耦误差时的等效杂波散射系数，C_t为发射互耦误差矩阵，a_t(θ_j)为θ_j方向的发射导向矢量；

(5c)采用步骤(4)中的交替迭代算法，求解包含发射互耦误差的代价函数，得到发射互耦矩阵C_t。

本发明具有如下优点：

1.本发明使用MIMO雷达的单次快拍回波数据，实现接收互耦误差和发射互耦误差的估计，有效解决了传统方法估计阵列互耦误差时对样本需求量大的问题。

2.本发明利用MIMO雷达波形的正交性，用接收互耦误差矩阵补偿回波数据，实现发射互耦误差自校正，解决了传统方法无法在线实时估计发射互耦误差的问题。

附图说明

图1为本发明的实现流程图；

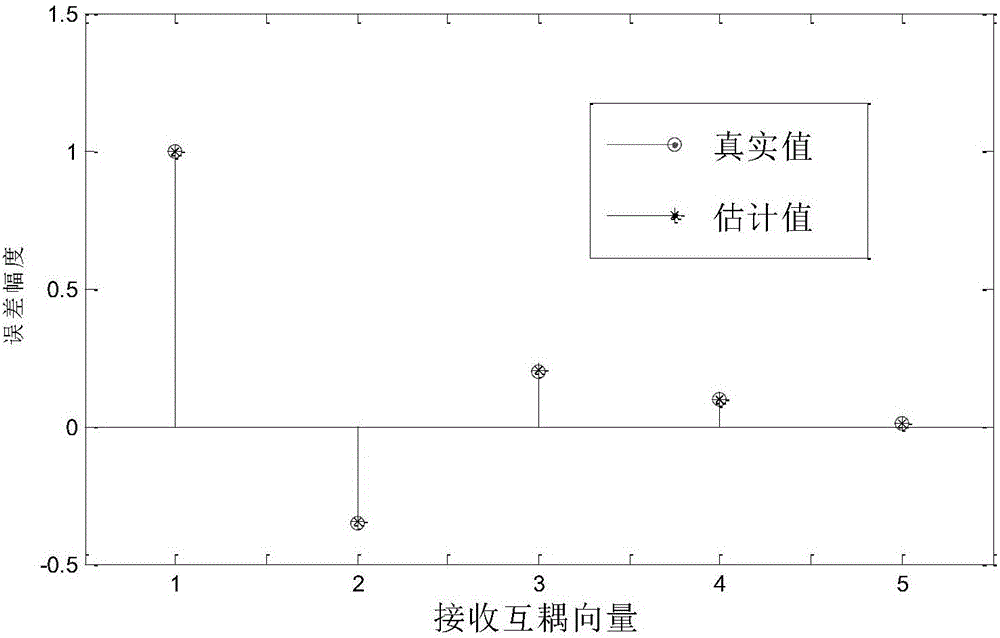
图2为本发明接收阵列互耦误差向量的实部真值与估计值的比较；

图3为本发明接收阵列互耦误差向量的虚部真值与估计值的比较；

图4为本发明发射阵列互耦误差向量的实部真值与估计值的比较；

图5为本发明发射阵列互耦误差向量的虚部真值与估计值的比较。

具体实施方式

以下结合附图对本发明的实施例及效果做进一步详细描述。

参照图1，本发明MIMO雷达收发阵列互耦误差自校正方法，其实现步骤如下：

步骤1，获取杂波回波数据。

(1a)设MIMO雷达发射和接收阵列的阵元数分别为N_t和N_r，接收互耦误差矩阵为C_r，发射互耦误差矩阵为C_t，对于均匀线阵而言，将C_r和C_t建模为如下对称带状Toeplitz矩阵：

接收互耦误差矩阵C_r中的元素由构成，且满足其中c_rw表示接收互耦误差矩阵C_r第一行的第w个元素，w＝1，2，...，p_r，其中p_r为接收互耦自由度，发射互耦误差矩阵C_t中的元素由构成，且满足其中c_tv表示发射互耦误差矩阵C_t第一行的第v个元素，v＝1，2，...，p_t，其中p_t为发射互耦自由度；

(1b)设MIMO雷达发射的正交信号为s＝[s₁ s₂…s_L]，其中L为码元长度，将某距离单元的J个静止不动杂波散射体回波基带信号表示为：

其中θ_j为第j个杂波散射体的方位，β_j为θ_j方向杂波散射体的散射系数，a_r(θ_j)为θ_j方向的接收导向矢量，a_t(θ_j)为θ_j方向的发射导向矢量，j＝1，2，...，J，C_r为接收互耦误差矩阵，C_t为发射互耦误差矩阵为，W为加性高斯白噪声；

(1c)对MIMO雷达回波数据X进行脉冲压缩，得到数据矩阵Y：

其中，(·)^H表示共轭转置，(·)^T表示转置，N＝WS^H为脉冲压缩后的回波噪声矩阵。

步骤2，构造伪协方差矩阵。

(2a)对数据矩阵Y进行取列操作，得到数据矩阵Y的第m列数据Y_m：

Y_m＝YΓ，

其中表示取第m列的数据；

(2b)根据接收互耦自由度p_r截取数据Y_m的中间有效孔径数据向量

其中Y_k，m表示数据Y_m的第k个元素，k＝p_r，p_r+1，...，N_r-p_r+1，N_r表示接收阵元的个数；

(2c)利用空间平滑算法，按照如下公式构造伪协方差矩阵：

其中y_i为数据向量的第i个元素，i＝1，2，...，n_r，n_r＝N_r-2(p_r-1)为接收阵列中间有效孔径阵元个数，p_r为接收阵列互耦自由度，N_r为接收阵元个数，*表示取共轭，q为划分的子阵个数，l为子阵阵元数。

步骤3，估计杂波散射体的方位信息。

(3a)对伪协方差矩阵R进行奇异值分解，得到J个大奇异值及由大奇异值对应的奇异向量张成的信号子空间U_s和l-J个小奇异值及由小奇异对应的奇异向量张成的噪声子空间U_n，J为杂波散射体个数，l为子阵阵元数；

(3b)利用信号子空间U_s与噪声子空间U_n的正交性，按照如下公式构造空间谱函数P(θ_j)：

其中，a_m(θ_j)是接收导向矢量a_r(θ_j)的前m行，a_r(θ_i)为θ_j方向的接收导向矢量，θ_j为第j个杂波散射体的方位，(·)^H表示共轭转置；

(3c)对空间谱函数P(θ_i)进行一维谱峰搜索，即可得到杂波散射体方位θ_j。

步骤4，交替迭代估计接收互耦误差矩阵C_r。

(4a)由步骤1得到的数据矩阵Y_m与步骤3估计的杂波散射体的方位θ_j，根据最小化重构误差准则，构造估计接收互耦误差的代价函数为：

其中，β′_j为θ_j方向杂波散射体的等效散射系数，C_r为接收互耦误差矩阵，a_r(θ_j)为θ_j方向的接收导向矢量，J为杂波散射体个数；

(4b)初始化：假设初始不存在互耦误差，即

(4c)计算第i次迭代中的等效散射系数将第i迭代得到的接收互耦误差矩阵带入接收互耦误差代价函数，采用最小二乘法计算第i次迭代中的等效散射系数

其中A_r＝[a_r(θ₁)a_r(θ₂)...a_r(θ_j)...a_r(θ_J)]，a_r(θ_j)为θ_j方向的接收导向矢量，(·)^H表示共轭转置，(·)^-1表示矩阵求逆；

(4d)更新接收互耦误差矩阵

(4d1)将接收互耦误差代价函数中的表示为：

其中是以互耦误差向量为变量的函数，互耦误差向量为接收互耦误差矩阵的第一列；

(4d2)将上述函数表示为：

其中，T(θ_j)是以θ_j为变量的函数矩阵，T(θ_j)＝T₁(θ_j)+T₂(θ_j)，

T₁(θ_j)为N_r×N_r维的第一函数矩阵，该矩阵的第b行第d列元素为：b＝1，2，...，N_r，d＝1，2，...，N_r，N_r为接收阵列阵元个数，a_b+d-1表示接收导向矢量a_r(θ_j)的第b+d-1个元素；

T₂(θ_j)为N_r×N_r维的第二函数矩阵，该矩阵的第b行第d列元素为：a_b-d+1表示接收导向矢量a_r(θ_j)的第b-d+1个元素；

(4d3)采用一阶Taylor展开对函数进行近似，得到以下近似式：

其中为第i次迭代得到的接收互耦误差向量，为接收互耦误差向量增量，将代回接收阵列互耦误差代价函数，即可得到接收互耦误差向量增量

(4d4)由第i次迭代得到的接收互耦误差向量和接收互耦误差向量增量得到接收互耦误差向量的初步更新值即：

(4d5)按的第一个元素对进行归一化，得到更新后的接收互耦误差向量再由构成更新后的接收互耦误差矩阵

(4e)重复步骤(4c)-(4d)，直至接收互耦误差代价函数不再减小，此时的接收互耦误差矩阵即为所求接收互耦误差矩阵C_r。

步骤5，估计发射互耦误差矩阵C_t。

(5a)对接收互耦误差矩阵C_r求逆并补偿回波数据矩阵Y，得到补偿后的回波矩阵Y′：

(5b)对Y′进行取行操作，得到第n行的数据Y_n′：

Y′_n＝ΛY′

其中表示取行操作；

(5c)以最小化重构误差为准则构建发射互耦误差的代价函数：

其中β_j″是θ_j方向发射互耦误差的等效杂波散射系数，C_t为发射互耦误差矩阵，a_t(θ_j)为θ_j方向的发射导向矢量，J为杂波散射体个数；

(5d)采用步骤(4)中的交替迭代算法，求解发射互耦误差的代价函数，得到发射互耦矩阵C_t。

本发明效果可以通过以下实验进一步证实：

1.实验场景：

设收发分置MIMO雷达接收阵元和发射阵元个数均为15，阵元间距为半波长，接收互耦误差向量为c_r＝[1-0.35+0.1j 0.2-0.16j 0.1+0.05j 0.01+0.01j]，发射互耦误差向量为c_t＝[1-0.3+0.1j 0.15-0.12j 0.05+0.02j 0.01-0.01j]，两个强杂波点分别位于40°和-20°方向，信噪比为50dB。

2.实验内容与结果

仿真一，在上述的实验场景下，采用本发明的方法对MIMO雷达接收阵列互耦误差进行估计，得到接收阵列互耦误差的实部的估计值与真实值的比较，结果如附图2所示；

仿真二，在上述的实验场景下，采用本发明的方法对MIMO雷达接收阵列互耦误差进行估计，得到接收阵列互耦误差的虚部的估计值与真实值的比较，结果如附图3所示；

从图2和图3中可以看出，本发明可以准确估计接收阵列互耦误差。

仿真三，在上述的实验场景下，采用本发明对MIMO雷达发射阵列互耦误差进行估计，得到接收阵列互耦误差的实部的估计值与真实值的比较，结果如附图4所示；

仿真四，在上述的实验场景下，采用本发明对MIMO雷达发射阵列互耦误差进行估计，得到接收阵列互耦误差的虚部的估计值与真实值的比较，结果如附图5所示。

从图4和图5中可以看出，本发明可以准确估计发射阵列互耦误差。

综上，本发明能够使用MIMO雷达的单次快拍回波数据，利用MIMO雷达波形的正交性，准确估计接收阵列互耦误差和发射阵列互耦误差，从而实现收发阵列互耦误差自校正。