一种应用于深水浅剖反射数据体的自动改正方法与流程

本发明涉及浅地层剖面反射数据体的处理，尤其涉及一种应用于深水浅剖反射数据体的自动改正方法。

背景技术：

随着我国向大洋及深远海领域挺近，深水浅地层剖面探测在海洋地质与地球物理调查中应用广泛，该探测可以提供深水海底浅部沉积地层的精细结构与空间展布情况，揭示深水海域浅部地质沉积过程及地质活动情况(如海底流体活动性、海床稳定性、构造活动性等)，为海洋地质学家提供连续直观的高分辨率海底浅部地质断面。

深水浅剖探测原理发展于近海浅水声学地层剖面探测技术，但又存在关键技术问题的改进，如能量不足、水平覆盖率低以及回波记录过长等问题。针对能量不足问题，深水浅剖可通过组合换能器阵来解决；针对声波水平覆盖率低的问题，可通过短时间连续快速发射和接收信号来解决；但是，反射回波记录时间过长比较棘手，解决好坏会直接影响回波的接收速率、数据存储与剖面质量，并影响声波信号的水平覆盖率。以2000米的海底水深为例，船载深水浅剖发射的声波信号到达海底面需要传播1.3秒(以1500m/s的声速计算)，声学换能器阵接收到反射回波需要双程传播时的2.6秒，加上海底下沉积地层的穿透双程时，单个声波Ping信号的记录时间要达到3秒以上，若以超高截止频率的32微秒采样率做高分辨率数据采样，其振幅样点数达到93750个，完全超出标准SEG-Y格式存储的32767个(二字节极限2¹⁵-1)样点极限。其次，过长的记录时间会影响声波发射间隔，如3秒的记录长度决定了声波信号的发射间隔要超过3秒，接收间隔也要超过3秒，否则有效反射数据体不能完整接收，这就造成声波信号间的水平间隔过大，若调查船以最低的4节速度航行，声波信号间的水平间隔达到6米。大间隔会使信号在海底面的水平覆盖率过低，造成地层反射同相轴的连续性变差，水深越深，发射间隔越大，声波水平覆盖率会更低，同时船速越快，水平覆盖率也同样会更低。为解决上述问题，目前国际成熟的深水浅剖系统都采用多Ping短时间连续发射和同步接收，接收时采用去除水体传播来压缩反射数据体的方法，即只接收海底面下一定深度范围内的有效反射数据体，保证声波信号短时间内的连续发射接收，并保证接收数据能以国际标准的SEG-Y格式文件正确存储。

去除水体中的声波传播时间需要实时追踪海底面反射，并将追踪结果实时写入SEG-Y记录道头参数中，根据实时追踪结果，系统会自动去除海底面以上水体中的无效传播数据，只接收海底面以下有效反射数据体，从而减少接收时间和存储数据量，提高声学信号的发射与接收速率。这样的提高带来了两个实际问题，一是海底面反射追踪的好坏会直接影响后续有效反射数据体的质量，二是SEG-Y格式存储的去水体传播剖面需要重新拼接，如图1所示的原始剖面。现场海底面实时追踪采集会存在多种干扰因素，如海况引起的调查船摇摆、深水浅剖的开角和灵敏度及参数设置等，这些干扰会产生错误的海底面追踪，如图2所示的突跳点，这些错误突跳点需要做人工消噪改正处理，否则影响后续的反射同相轴拼接。传统的方法如先验信息法、滑动平均法、中值滤波法、多项式拟合法等只能改正单点或连续几个点的突跳情况，不能改正区块性连片多点的错误追踪结果，改正同时还会破坏突跳点附近的有效值，给后续的剖面拼接处理带来误差。有效改正了海底面反射实时追踪结果，还需要对SEG-Y存储格式的反射剖面作同相轴拼接处理，拼接处理要利用海底面追踪结果，以成组搬家的方法来正确拼接反射同相轴，但对深海水深变化非常大的数据体，最深与最浅水深处的反射数据体因改正量太大，会出现搬家搬出有效改正范围的问题，从而拼接不出完整的地层剖面，因此，解决成组搬家的有效实现方法也非常重要。

由上述可知，目前的深水浅剖数据处理方法面临以下两个问题：一是数据采集中实时追踪的海底面反射干扰噪音压制问题，二是深水浅剖去水体反射后剖面同相轴的有效拼接问题。因此，针对深水浅剖探测遇到的特殊问题，现在亟需一种简单有效的改正海底面错误追踪结果，并恢复深水浅剖实际剖面形态的综合校正方法，为深水浅剖探测数据的有效应用提供基础。

技术实现要素：

本发明所要解决的技术问题在于，提供一种应用于深水浅剖反射数据体的自动改正方法，其能够对深水浅剖海底面反射的追踪结果进行有效改正，并对反射同相轴进行可靠拼接，进而恢复深水浅剖实际地层剖面形态。

为了解决上述技术问题，本发明提供了一种应用于深水浅剖反射数据体的自动改正方法，其包括步骤：

结合邻近点双差值阈值自动定位消噪法改正深水浅剖海底面反射深度曲线；

根据改正后的海底面反射深度曲线进行反射剖面的重新拼接，得到海底地层真实反射剖面图像。

进一步地，进行反射剖面拼接处理时，是利用极值扩容成组搬家法实现的。

其中，所述结合邻近点双差值阈值自动定位消噪法改正海底面反射深度曲线的步骤，包括步骤：

根据所述海底面反射深度曲线中前后邻近点进行双差值运算，并根据双差值运算结果获得异常突跳点；

根据所述异常突跳点推算突跳阈值，并根据所述突跳阈值反推所述海底面反射追踪曲线中所有突跳点的个数，及每个突跳点的分布位置；

根据反推出的突跳点的个数和每个突跳点的分布位置，对所述海底面反射追踪曲线进行校正。

其中，根据所述海底面反射深度曲线中前后邻近点进行双差值运算，得到异常突跳点的步骤，包括步骤：

构建原始数组A_i以存储所述海底面反射追踪结果所对应的原始数据；

根据原始数据A_i进行第一次差值运算，得到第一次差值数组D_j；

对所述第一次差值数组D_j按照预设规则进行排序，得到排序后的新的一次差值数组B_k；

对排序后的一次差值数组B_k进行第二次差值，得到二次差值数组DD_m；

根据所述二次差值数组DD_m中的最大值获取对应的异常突跳点。

其中，根据所述异常突跳点推算突跳阈值，并根据所述突跳阈值反推所述海底面反射追踪曲线中所有的突跳点个数，及每个突跳点的分布位置的步骤，具体包括步骤：

根据所述异常突跳点所在位置，反推一次差值排序号数组B_k所对应的突跳阈值；

根据所述一次差值排序后数组B_k的突跳阈值，反推第一次差值排序前数组D_j中的所有突跳点及对应位置；

根据所述第一差值数组D_j中的突跳点反推所述原始数组Ai中的所有突跳点及对应位置。

进一步地，对原始数据Ai进行干扰噪音的自动识别及压制处理，压制后再以各个突跳点前后有效追踪点的线性插值替代干扰噪音以进行有效改正。

其中，利用极值扩容成组搬家法进行反射剖面拼接的步骤，具体包括步骤：

根据改正后的海底面反射深度曲线进行极值计算，分别得到海底面最深值与最浅值；

根据所述最深值和最浅值扩充调用深水浅剖数据的存储空间，然后进行成组搬家运算。

对应于上述应用于深水浅剖反射数据体的自动改正方法，本发明提供了相应的改正装置，其包括：

改正模块，用于结合邻近点双差值阈值自动定位消噪法改正深水海底面反射深度曲线；

拼接模块，用于利用改正后的海底面反射深度曲线进行反射剖面的拼接处理，得到深水海底反射真实地层剖面图像。

其中，所述改正模块包括：

差值计算子模块，用于根据所述海底面反射深度曲线中前后邻近点进行双差值运算，并根据双差值运算结果获得异常突跳点；

反推子模块，用于根据获得的异常突跳点推算突跳阈值，并根据所述突跳阈值和双差值运算结果反推所述海底面反射深度曲线中所有突跳点的个数，及每个突跳点的分布位置；

曲线改正子模块，用于根据反推出的突跳点的个数和每个突跳点的分布位置，对所述海底面反射深度曲线进行自动改正。

其中，所述拼接模块包括：

极值计算子模块，用于根据改正后的海底面反射深度曲线进行极值计算，分别得到海底面最深值与最浅值；

空间扩充子模块，用于根据所述最深值和最浅值扩充调用深水浅剖数据的存储空间；

搬家子模块，用于根据扩充后的存储空间进行成组搬家运算。实施本发明的有益效果

本发明的方法，通过利用邻近点双差值阈值自动定位消噪法对该反射深度曲线进行改正，以自动消除干扰噪音引起的海底面反射错误追踪；进一步地，进行反射剖面同相轴的拼接处理，采用提出的极值扩容成组搬家法进行拼接，即先扩充深水浅剖调用数据的存储空间，避免搬家越界，进而完成对反射剖面的拼接，恢复实际反射地层的剖面形态。

附图说明

为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例或现有技术描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其他的附图。

图1是经海底实时追踪去水体传播后存储的标准SEG-Y数据原始剖面示意图；

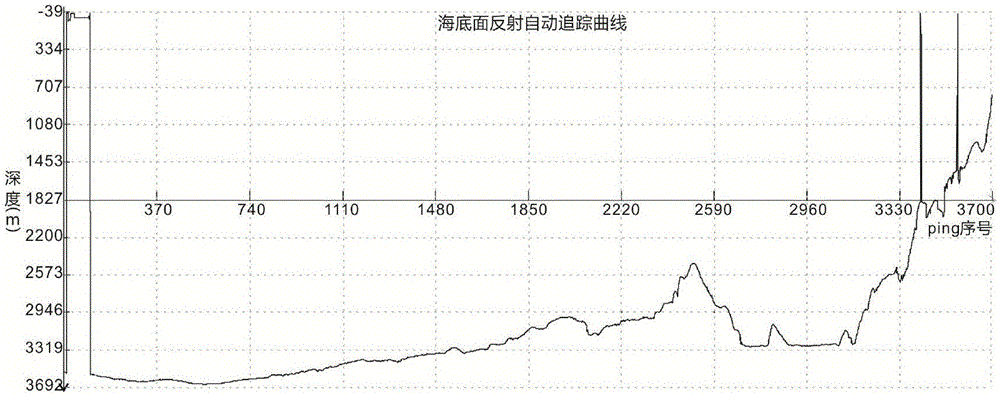
图2是深水浅剖野外实时追踪的海底面反射深度曲线示意图；

图3是本发明的一种应用于深水浅剖反射数据体的自动改正方法的一实施例的流程图；

图4是图3中步骤S13的一实施例的流程图；

图5是图3中步骤S13、S15的另一实施例的流程图；

图6a、图6b、图6c和图6d分别是反映海底面反射的原始数组A_i，第一次差值数组D_j，经过排序后一次差值数组B_k，以及二次差值数组DD_m的示意图；

图7a、图7b、图7c和图7d分别是反映二次差值数组DD_m中最大值，一次差值排序后数组B_k中的突跳阈值，第一次差值排序前数组D_j中各个突跳点，以及原始数值经线性插值改正后的曲线示意图；

图8是本发明中的极值扩容成组搬家实现剖面拼接的示意图；

图9是本发明的一种用于深水浅剖反射数据体的改正装置的一实施例的功能模块图；

图10是图2中的原始曲线经过改正之后的示意图；

图11是图1中的SEG-Y原始剖面经校正之后的结果示意图。

具体实施方式

下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有作出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。

本发明的深水浅剖反射数据体自动改正方法及其装置，主要利用邻近点双差值阈值自动定位消噪法对野外实时追踪的海底面反射曲线进行自动改正，然后进行极值扩容成组搬家法实现反射剖面的有效拼接。其中，邻近点双差值运算的主要目的是消除背景值，突显异常突跳点的幅值，从而可推算突跳阈值，然后利用阈值反推各个突跳点所在位置，并对追踪曲线进行自动改正；进一步地，当改正完成后，再进行同相轴拼接处理，采用极值扩容成组搬家法来实现，即在成组搬家前，先对上面改正曲线进行极值判断，获得海底面最深与最浅值，再利用这两个极值扩充深水浅剖数据的存储空间，避免成组搬家越界，最后完成反射同相轴的有效拼接，恢复实际反射地层的剖面形态。

实施例一

参见图3，为本发明的一种应用于深水浅剖反射数据体的自动改正方法的一实施例的流程图，具体实施时，该方法包括步骤：

S13，结合邻近点双差值阈值自动定位消噪法改正野外实时追踪的海底面反射深度曲线。

本实施中，系统是根据深水浅剖野外实时追踪的海底面反射深度值绘制相关曲线。具体地，通过从SEG-Y记录文件中正确读取野外采集海底面反射实时追踪值，然后绘制相应深度曲线，即深水浅剖实时追踪的海底面反射深度曲线。

然而由于干扰噪音的存在，此时绘制的曲线通常含有错误数据，如图2所示，该图为全海深浅剖Bathy-2010系统采集的深水浅剖数据，其实时追踪的海底面深度曲线最深超过3690米，最浅只有740米左右，深度曲线上存在三处明显的异常值，即干扰噪音导致的突跳点，第一处为一连续干扰突跳点，连续的Ping序号超过100，表现为一区块性连续追踪错误，第二处为连续3个Ping序号追踪错误，第三处为单个Ping序号追踪错误，为了还原实际海底面，需要对该深度曲线进行改正。

由于曲线中突跳点与曲线中各个有效追踪点(即不受干扰噪音影响的有效追踪数据)之间的幅值差别较大，因此，本实施例中，利用邻近点两次差值运算来消除背景值，从而突显异常突跳点的幅值，以准确获得突跳阈值，进而根据该突跳阈值来反推各个突跳点的分布位置，再根据各个突跳点的分布位置(即干扰噪音突跳点所在位置)进行自动改正，从而消除深水采集各种干扰引起的错误海底面追踪，改正结果如图所示10，该图为图2中的原始曲线经过本实施例中的邻近点双差值阈值自动定位消噪法改正之后获得的曲线，图中3处错误追踪都获得有效压制，深度曲线整体形态连续，无大的突跳异常。

参见图4，为本实施例中步骤S13的一实施例的流程图，具体地，该步骤S13包括步骤：

S31，根据所绘制的海底面反射深度曲线中前后邻近点进行双差值运算，得到异常突跳点。

本实施例中，进行双差值运算，具体包括：

首先，构建原始数组A_i(1≤i≤N)＝[A₁,A_2,A₃,...,A_N]以存储上述反射追踪曲线对应的各个原始数据。在一具体实施例中，如图6a中所示的海底面追踪深度样点原始曲线，该曲线上存在两处错误追踪突跳，一处为单点突跳，另一处为连续多点突跳，针对该曲线对应的原始数据，构建内存数组A_{i(1≤i≤15)}＝[A₁,A_2,A₃,...,A₁₅]存储各个原始数据。

其次，对该原始数组A_i(1≤i≤N)＝[A₁,A_2,A₃,...,A_N]进行第一次差值运算，得到第一次差值数组D_j(1≤j＜N)＝[D₁,D_2,D3,…,D_N-1]，即D_{j(j＝i,且1≤j＜N)}＝A_{i+1(1≤i≤N)}-A_i(1≤i≤N)。在一具体实施例中，为了消除正常背景值，需要先将原始数组A_i中前后相邻的两项进行第一次差值计算D_{j(j＝i,且1≤j＜N)}＝A_{i+1(1≤i≤N)}-A_i(1≤i≤N)，从而得到相应的第一差值数组D_{j(j＝i,且1≤j＜15)}＝[D₁,D_2,D3,...,D₁₄]＝[A₂-A₁,A₃-A₂,…,A₁₅-A₁₄]，如图6b所示。

再者，为消除多个异常值的存在并进一步压制正常背景值，为后续的第二次差值运算做准备，按照预设规则，如按照从大到小的顺序，将第一次差值数组D_j(1≤j＜N)进行排列，得到排序后的一次差值数组：B_k(1≤k＜N)＝SORT(D_j)＝[B₁,B₂,B₃,...,B₁₄]。在一具体实施例中，如图6c所示，对第一次差值结果进行排序，得到新的排序后一次差值数组：B_k＝SORT(D_j)＝[B₁,B₂,B₃,...,B₁₄]＝[D₃,D₄,D₉,D₁₂,D₁₁,...D₂]。

然后，对排序后的一次差值数组B_k进行第二次差值计算得到二次差值数组并计算该二次差值数组中的最大值，该最大值所对应的点即为异常突跳点。在一具体实施例中，参见图6d，经过第二次差值运算之后得到的二次差值数组，二次差值后幅值减少了很多，即正常背景值非常小，噪音压制处理的干扰因素基本消除，并使异常突跳点由多个变为1个，即二次差值数组中的最大差值DD₄所对应的突跳点，而该异常突跳点为自动判断阈值的获取提供了关键。

S33，根据上述异常突跳点推算突跳阈值，并根据该突跳阈值反推所有突跳点的个数及每个突跳点的分布位置。

由于经过上述步骤S31中的双差值运算后，正常有效值的幅值进一步消减，并根据该二次差值数组DD_m中的最大值获得对应的异常突跳点，从而可根据该异常突跳点的分布位置反推各计算过程中一次差值排序后数组B_k和第一次差值数组Dj中各个异常突跳点的位置，即反推上述的双差值计算过程，进而获得原始数组A_i中所有的突跳点位置及个数，具体地：

首先，根据该异常突跳点反推一次差值排序后数组B_k＝SORT(D_j)所对应的突跳阈值。在一具体实施例中，由于数组中每个数值都有对应的序号，因此可根据该二次差值数组DD_m中的最大差值的横轴序号，然后利用该最大差值的横轴序号来反推差值数组B_k中所对应的突跳点的位置序号，参见图7a，例如二次差值数组DD_m中的最大差值为DD₄，其对应的横轴序号为4，且DD₄＝B₅-B₄，则根据该最大差值的横轴序号来反推一次差值排序已数组B_k＝SORT(D_j)中所对应的突跳点的位置序号4和5，且选择其中幅值较大的点，即B₄，所对应的数值为突跳阈值，参见图7b。

然后，根据该突跳阈值和各个差值(即差值数组D_j中的各个差值)，反推第一次差值数组D_j中突跳点的个数，以及每个突跳点的分布位置。在一具体实施例中，参见图7c，由于突跳阈值已确定为B₄＝D₁₂，由此可以判断出排序前的第一次差值数组D_j中的所有突跳点及对应位置，即所有数值大于或等于B₄＝D₁₂的均为突跳点：D₃，D₄，D₉，D₁₂，又D_j(1≤j＜N)＝A_{i+1(1≤i≤N)}-A_i(1≤i≤N)，因此，基于相同的原理，通过这些突跳点位置，就可以反推原始数据A_i中对应的异常点位置：A3，A4，A5，A9，A10，A11，A12，A13。

S35，根据反推出的突跳点的个数和每个突跳点的分布位置，对海底面反射追踪曲线进行改正。

本实施例中，由于原始数组元素内部相减运算获得的新内存数组时会使数组元素减少1个，第二次相减运算后会比原始数据少2个，例如，原始数组A_i的相减运算使内存数组成员减少1项，突跳点个数就不包括第一个异常点位置，也就是说，在进行反推运算时，需要特别注意数组元素的个数及异常点对应的位置序号，例如A_i与D_j数组元素序号的匹配问题。最后，可以对原始数组A_i进行干扰噪音的自动识别与压制处理，然后再以干扰噪音所对应的各个突跳点前后有效有效追踪点的线性插值替代干扰噪音，参见图7d，从而获得最后可靠的改正结果。

S15，根据改正后的海底面反射深度曲线进行反射剖面的拼接处理，得到深水浅剖海底地层真实的反射剖面图像。

本实施例中，通过邻近点两次差值运算的目的是消除背景值，突显异常突跳点的幅值，从而可根据其自动获得突跳阈值，然后反推各个突跳点所在位置，并对曲线进行改正，最后对反射剖面同相轴进行有效拼接，恢复实际反射地层的剖面形态。

实施例二

对反射深度曲线进行校正之后，还需对去水体后的SEG-Y数据做反射同相轴拼接处理，否则得到的剖面形态与实际情况不符。而拼接处理的算法基础是数据体成组搬家，对于深水浅剖，由于深水海底地形复杂多变，存在星罗棋布的礁滩与纵横交错的槽谷，以及陡峭挺拔的海山，造成海底地形快速变化，给深水浅剖的同相轴拼接处理带来困难。另外，由于SEG-Y格式文件对单个Ping记录样点长度的限制，成组搬家会出现搬出记录数据范围的问题，如记录长度为8000个样点的深水浅剖数据，测线最浅处为740米左右，而最深处达到3700米，如此大跨度的水深地形，若以常规的成组搬家方法肯定会使内存数组越界，造成泄露错误。因此，在进行拼接之前，需要扩充内存数组容量，突破SEG-Y存储文件原始大小，给深水浅剖拼接处理中的成组搬家提供充足的内存空间。然而，存储空间的扩容也不能随意进行，扩充不够，搬家处理照样会越界，扩充太多，会造成存储空间的浪费，甚至是系统的崩溃。

基于上述实施例一中的改正结果，本发明进一步解释同相轴拼接处理方法，下面结合具体实施例和附图进行详细的说明。

本实施例中的反射剖面拼接处理方法，是利用改正后的海底面反射深度曲线，通过水深极值范围来设置存储容量的扩充大小，从而有效管理内存空间的开销和成组搬家的范围，保证剖面拼接的完整性。具体地，本实施例中，海底地层反射数据体的自动改正方法包括上述实施例一中的各个步骤，不同的是，本实施例中的该自动改正方法在进行反射剖面拼接时，是利用极值扩容成组搬家法实现剖面拼接的方法。

参见图5，为本发明的深水浅剖反射数据体校正方法的实施例的流程图，具体地，本实施例中，进行拼接的步骤，具体包括：

S51，根据改正后的海底面反射深度曲线进行极值计算，分别得到海底面最深值与最浅值。

S53，根据最深值和最浅值扩充深水浅剖数据的存储空间，然后进行成组搬家运算。

本实施例中，在进行成组搬家运算时，搬动的偏移量是根据当前Ping海底面追踪深度与最浅海底面之差值计算得到的。

本实施例中，通过采用极值扩容成组搬家法进行反射剖面的拼接处理，即在成组搬家前，先对上面改正曲线进行极值判断，获得海底面最深与最浅值，利用这两个极值来扩充深水浅剖数据的调用存储空间，避免成组搬家越界，从而完成对反射剖面同相轴的有效拼接，进而恢复实际反射地层的剖面形态，如图8所示的示意图。

实施例三

对应于上述实施例一中的自动改正方法，本发明还提供了一种改正装置，下面结合具体实施例和附图进行详细的说明。

参见图9，为本发明的一种用于深水浅剖反射数据体的改正装置，具体地，该改正装置包括：

校正模块，用于结合邻近点双差值阈值自动定位消噪法改正系统所绘制的海底面反射深度曲线；本实施中，该海底面反射深度曲线是系统根据深水浅剖野外实时追踪的有效数据体进行绘制的，然而由于干扰等，此时绘制的曲线通常含有错误数据，如图所示2，深度曲线上存在三处明显的突跳点，即干扰噪音，第一处为一连续干扰突跳点，连续的Ping序号超过100，因此为一区块性追踪错误，第二处为连续3个Ping序号追踪错误，第三处为单个Ping序号追踪错误。为了能够有效还原海底面剖面，需要对该深度曲线进行改正。

拼接模块，用于根据改正后的海底面反射深度曲线进行反射剖面拼接，得到海底地层真实的反射剖面图像。

参见图9，本实施例中，该校正模块具体包括：

差值计算子模块，用于根据上述海底面反射深度曲线中前后邻近点进行双差值运算，并根据双差值运算结果获得异常突跳点；具体地，该差值计算子模块首先构建原始数组A_i，以存储上述反射追踪曲线对应的原始数据；然后根据原始数据A_i进行第一次差值运算，得到第一差值数组D_j；再对该第一差值数组D_j按照预设规则(如从大到小的顺序)进行排序，得到排序后新的一次差值数组B_k；并对排序后得到的一差值数组B_k进行第二次差值，得到二次差值数组DD_m；最后根据二次差值数组DD_m中的最大值获取对应的异常突跳点；

反推子模块，用于根据获得的异常突跳点推算突跳阈值，并根据推算的突跳阈值和上述的双差值运算结果反推海底面反射深度曲线中所有突跳点的个数，及每个突跳点的分布位置；具体地，该反推子模块先根据上述异常突跳点所在位置，反推排序后一次差值数组B_k所对应的突跳阈值；再根据排序后一次差值数组B_k的突跳阈值，反推第一次差值数组D_j中的所有突跳点及对应位置，并根据第一次差值数组D_j中的突跳点反推所述原始数组Ai中的所有突跳点及对应位置；

曲线校正子模块，用于根据反推出的突跳点的个数和每个突跳点的分布位置，对所述海底面反射深度曲线进行校正；具体地，该曲线校正子模块是以各个突跳点前后有效值的线性插值替代干扰噪音以进行校正的。

由于对反射深度曲线进行校正之后，还需对去水体后的SEG-Y数据做反射剖面的同相轴拼接处理，即进行数据体成组搬家。但由于深水海底地形复杂多变，海底地形变化迅速，给深水浅剖的同相轴拼接处理带来困难。并且，由于SEG-Y格式文件对单个Ping记录样点长度的限制，成组搬家会出现搬出记录数据范围的问题，若以常规的成组搬家方法肯定会使内存数组越界，造成泄露错误。因此，在进行拼接之前，需要扩充内存数组容量，突破SEG-Y存储文件原始大小，给深水浅剖拼接处理中的成组搬家提供充足的内存空间。然而，存储空间的扩容也不能随意进行，扩充不够，搬家处理照样会越界，扩充太多，会造成存储空间的浪费，甚至是系统的崩溃。因此，本实施例中的该拼接模块在进行拼接时，是先根据校正后的海底面反射深度曲线计算水深极值范围，从而根据极值来设置存储容量扩充的大小，并有效管理内存空间的开销和成组搬家的范围，保证剖面拼接的完整性。具体地，参见图9，本实施例中，该拼接模块包括：

极值计算子模块，用于根据校正后的海底面反射深度曲线进行极值计算，分别得到海底面最深值与最浅值；

扩充子模块，用于根据上述的最深值和最浅值来扩充深水浅剖数据调用的存储空间；

搬家子模块，用于根据扩充后的存储空间进行成组搬家运算；具体地，该搬家子模块进行数值搬家时，其搬动的偏移量是根据当前Ping与海底面最浅值之间的差值来确定的。

本实施例中，该改正模块可直接应用于现有的海底地层剖面绘制系统中，其通过利用邻近点双差值阈值自动定位消噪法对海底面反射深度曲线进行校正；同时，还通过拼接模块利用海底面的两个极值来扩充深水浅剖数据的调用存储空间，避免成组搬家越界，从而完成对反射剖面的有效拼接，进而恢复深海浅地层反射的实际剖面形态，如图11所示。

以上所揭露的仅为本发明较佳实施例而已，当然不能以此来限定本发明之权利范围，本领域普通技术人员可以理解实现上述实施例的全部或部分流程，并依本发明权利要求所作的等同变化，仍属于发明所涵盖的范围。