一种大角度机动下带挠性附件航天器转动惯量在轨辨识方法与流程
本发明涉及一种大角度机动下带挠性附件航天器转动惯量在轨辨识方法。
背景技术:
传统方法做带挠性附件航天器转动惯量辨识的问题,将待辨识参数作为状态量,增广到状态方程中的方法。而扩展卡尔曼滤波用于参数估计中,往往因为没有计入参数的变化对增益的影响,容易导致有偏估计或发散。本发明的方法是利用广义的卡尔曼滤波估计振动模态这一状态量,再用最小二乘法做参数估计,不停地循环,直至结果收敛。
传统的方法直接用扩展卡尔曼滤波做参数估计,没有计入参数的变化对增益的影响,未能体现卡尔曼滤波的滤波修正的效果,收敛速度非常的慢。本发明仅用广义卡尔曼滤波做状态估计,状态估计的效果较好。而且为了进一步提高计算效率,本发明采用多步广义卡尔曼滤波与一步最小二乘法并发递推的方法。
传统方法在计算主惯量的精度较好,但是计算惯性积的精度较差。
技术实现要素:
根据现有技术存在的问题,本发明公开了一种大角度机动下带挠性附件航天器转动惯量在轨辨识方法包括以下步骤:
s1:根据航天器的姿态动力学方程与挠性附件的运动方程,建立系统的动力学模型,再把非线性的动力学模型描述成状态空间的形式,将状态空间方程进行离散化、线性化处理,使系统状态空间方程可适用于广义卡尔曼滤波,估计振动模态;
s2:利用陀螺仪采集的姿态角速度数据和航天器做机动的控制力矩数据,采用广义卡尔曼滤波算法估计出挠性附件的振动模态及其导数,再代入挠性附件运动方程估计出振动模态的二阶导数;
s3:将带挠性附件卫星的姿态动力学方程写成最小二乘的描述形式,利用s2估计出的振动模态二阶导数
s4:将s2中广义卡尔曼滤波算法估计出振动模态与s3中最小二乘辨识出的转动惯量互相调用,循环s2和s3步骤,并发递推,获得转动惯量的辨识值。为了提高了算法的效率,采用多步广义卡尔曼滤波与一步最小二乘法结合并发地递推。
进一步的,s1中:根据航天器的姿态动力学方程(1)与挠性附件的运动方程(2)建立系统的动力学模型,再把系统的动力学模型描述成状态空间的形式(3)采用如下方式:
当卫星姿态角变化时,带挠性附件卫星姿态动力学和挠性附件运动方程为
其中:
这样带挠性附件卫星系统的状态空间方程
其中,f(jsat,xa)=d-1axa,ba(jsat)=d-1b;
i是单位阵;u是输入、为控制力矩;
离散化的非线性状态空间方程为:
其中,f=ts*f(jsat,xk)+xk;g=ts*ba(jsat);ts为采样的周期;xk表示第k次状态。
线性化后的状态空间方程为:
其中,
进一步的,s3中具体采用如下方式:
将待辨识的转动惯量参数表示成标称值和残差值相加的形式,
jsat=jnom+δj(6)
其中,jnom是转动惯量的标称值,也可理解为整个递推算法的初值;δj是转动惯量随递推迭代变化的那部分值。
将式(6)代入式(1)中,得到
由式(7)可得到带挠性附件卫星的姿态动力学方程的最小二乘的描述形式
ajxj=bj(8)
其中
由于采用了上述技术方案,本发明提供的一种大角度机动下带挠性附件航天器转动惯量在轨辨识方法,具有的有益效果:
(1)本发明针对大角度机动下带挠性附件航天器转动惯量辨识的问题,采用了非线性的刚柔耦合模型作为辨识估计的系统状态方程。本发明将广义卡尔曼滤波与最小二乘法结合起来,并发递推,巧妙地把状态估计与参数估计相结合,最终辨识出航天器的转动惯量参数。递推辨识的算法占用的计算空间较小,运算速度较快,且辨识结果的精度较高。
(2)在广义卡尔曼滤波算法估计出的振动模态与最小二乘辨识出的转动惯量互相调用过程中,本发明采用多步广义卡尔曼滤波与一步最小二乘法结合来并发地递推,进一步提高了算法的效率。
(3)本发明辨识可航天器转动惯量矩阵,同时估计出了卫星挠性附件的振动模态,可进一步了解航天器在轨运行时的结构特性。
(4)本发明的方法可以在航天器做姿态调整时(或由动力装置主动施加力矩),利用星体自带的测量设备,测量出或间接测量出姿态角度、角速度与角加速度,即可辨识出航天器的转动惯量,工程可行性强。
附图说明
为了更清楚地说明本申请实施例或现有技术中的技术方案,下面将对实施例或现有技术描述中所需要使用的附图作简单地介绍,显而易见地,下面描述中的附图仅仅是本申请中记载的一些实施例,对于本领域普通技术人员来讲,在不付出创造性劳动的前提下,还可以根据这些附图获得其他的附图。
图1为本发明的方法的流程图;
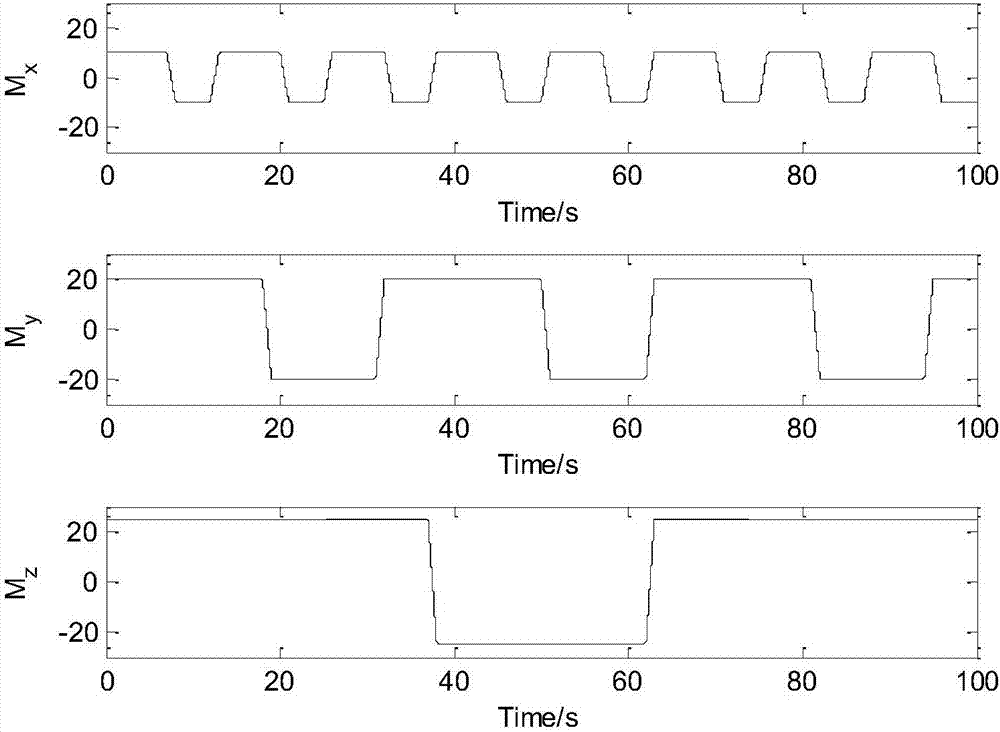
图2为本发明中实施例中输入的控制力矩的示意图;
图3为本发明中实施例中转动惯量辨识的结果示意图。
具体实施方式
为使本发明的技术方案和优点更加清楚,下面结合本发明实施例中的附图,对本发明实施例中的技术方案进行清楚完整的描述:
如图1所示的一种大角度机动下带挠性附件航天器转动惯量在轨辨识方法,具体步骤如下:
s1:根据航天器的姿态动力学方程与挠性附件的运动方程,建立系统的动力学模型,再把非线性的动力学模型描述成状态空间的形式,将状态空间方程进行离散化、线性化处理,使系统状态空间方程可适用于广义卡尔曼滤波,估计振动模态。
当卫星姿态角变化时,带挠性附件卫星姿态动力学和挠性附件运动方程为
式中:
式(1)中
在带挠性附件卫星转动惯量的最小二乘描述形式中,当挠性附件振动模态已知时才可利用最小二乘法对卫星转动惯量参数进行辨识。对于挠性附件振动模态,不能直接测量得到,本节将通过广义卡尔曼滤波算法进行估计。
将带挠性附件卫星动力学方程式(1)和(2)转化为一阶微分方程的形式
其中
设f(jsat,xa)=d-1axa,ba(jsat)=d-1b,式(3)可以表示为
引入测量方程
ya=caxa(5)
其中
测量值为姿态角和姿态角速度。
这样带挠性附件卫星的动力学方程转化为了状态空间方程的形式
采用差分将上述系统离散化,
整理,得
xk+1=(ts*f(jsat,xk)+xk)+ts*ba(jsat)u(8)
令f=ts*f(jsat,xk)+xkg=ts*ba(jsat)
得到离散化的非线性状态空间方程,
非线性方程线性化,
其中p=1,2,3。
线性化后的方程
s2:利用陀螺仪采集的姿态角速度数据和航天器做机动的控制力矩数据,采用广义卡尔曼滤波算法估计出挠性附件的振动模态及其导数,再结合挠性附件运动方程估计出振动模态的二阶导数。
s1中的挠性附件卫星动力学方程转化为离散系统状态空间方程的形式,可以通过状态估计的方法可以同时得到姿态角和振动模态的估计值。本发明将利用广义卡尔曼滤波算法估计出振动模态η及其一阶导数
s3:将卫星的姿态动力学方程写成最小二乘的描述形式,利用s2估计出的振动模态二阶导数
将待辨识的转动惯量参数表示成标称值和残差值相加的形式,
jsat=jnom+δj(1)
将式(6)代入式(1)中,得到
式(7)等号左边的处理为
式(7)可以表示为
ajxj=bj(5)
其中
式(8)即为带挠性附件卫星转动惯量的最小二乘描述形式,与刚体卫星转动惯量的最小二乘描述形式相比,其中
s4:将s2中广义卡尔曼滤波算法估计出振动模态与s3中最小二乘辨识出的转动惯量互相调用,循环s2和s3步骤,并发递推,获得转动惯量的辨识值。很快就收敛于真实值。为了提高了算法的效率,采用多步广义卡尔曼滤波与一步最小二乘法结合并发地递推。
在上面推导的质量特性参数jsat的最小二乘描述形式和挠性附件振动模态η估计的广义卡尔曼滤波算法中,均是假设其它参数和状态都是已知的情况下对未知参数或状态进行估计。而卫星在轨运行过程中,转动惯量jsat和挠性附件振动模态η的真实值都是未知的。为此,采用多变量并发递推的思想,将转动惯量的最小二乘描述形式和挠性附件振动模态η的状态估计相结合,提出一种带挠性附件卫星转动惯量在轨辨识的并发递推算法。
本发明基于多变量并发递推算法的思想,将转动惯量jsat和挠性附件振动模态η参数辨识结果互相调用,结合最小二乘法和广义卡尔曼滤波算法,形成完整的并发递推算法。因为采用差分离散,广义卡尔曼滤波存在一定的近似,因此为了提高精度,滤波估计的采样周期应该较短。为了提高算法的效率,这里采用q步广义卡尔曼滤波,1步最小二乘作为一个循环,一共循环n次。其算法的具体流程,如图1:先用广义卡尔曼滤波进行振动模态状态估计q次,体现为图1中内环;再用最小二乘进行转动惯量参数的辨识,体现为图1中外环。反复迭代递推,即可得到转动惯量的辨识值。
实施例:
仿真算例选取某型号通信卫星模型。卫星主要的挠性附件为对称的两个太阳能帆板,每个太阳能帆板长8.1米,质量36.6kg,卫星展开总跨度18.4米,总质量2850.8kg。该卫星是典型的带有大型挠性附件的卫星。
该卫星模型的动力学分析表明,附件振动对整星动力学特性的影响主要由左右两侧帆板的第一阶振动模态决定,因此本发明算例中只考虑第一阶模态的影响,忽略高阶模态。左右两侧帆板的一阶模态频率均为1.2754,模态阻尼比为0.005,转动惯量真实值jreal和帆板转动刚柔耦合系数矩阵prot为
为了验证本发明并发递推算法的有效性,用matlab软件进行了仿真。由于卫星通常装配喷气系统,来实现姿态调整,所以仿真的输入力矩为占空比为60的方波力矩信号,如图2所示。姿态角速度的初始值为
表1转动惯量辨识结果(绝对误差、相对误差)
图3中传统方法kfls(不考虑非线性影响的最小二乘与卡尔曼滤波并发递推方法)辨识出的结果振荡严重,完全辨识不出结果。而用本发明提出ekfls递推算法得到的辨识结果都很接近真实值,从表1中可以看出转动惯量辨识值的相对误差都在3%以内。由于采用了多步广义卡尔曼滤波与一步最小二乘循环递推的算法,辨识结果很快的收敛,计算效率较高。如果在轨测量设备(角速度陀螺)的采样时间能更短,辨识的效果则会更好。仿真结果证明当卫星做大角度机动时,应该考虑非线性项的影响,而本发明提出的最小二乘法和多步广义卡尔曼滤波相结合的并发递推算法则是处理带挠性附件卫星做大角度机动的转动惯量参数辨识的有效方法。
以上所述,仅为本发明较佳的具体实施方式,但本发明的保护范围并不局限于此,任何熟悉本技术领域的技术人员在本发明揭露的技术范围内,根据本发明的技术方案及其发明构思加以等同替换或改变,都应涵盖在本发明的保护范围之内。
- 还没有人留言评论。精彩留言会获得点赞!