载荷约束下圆柱滚子轴承内圈径向跳动预测方法与流程

本发明涉及圆柱滚子轴承运动精度预测方法技术领域，具体涉及一种载荷约束下圆柱滚子轴承内圈径向跳动预测方法。

背景技术：

载荷约束下圆柱滚子轴承内圈径向跳动预测方法是为了根据已知或给定轴承元件形状误差预测载荷作用下轴承内圈径向跳动及其历程。

对于内圈转动的滚动轴承，内圈径向跳动是衡量轴承动态性能的关键参数之一，但这个评价参数只是单一数值，并不能完全反映轴承在回转过程中旋转精度的动态特征，而轴承径向跳动历程则能较好地展现轴承旋转过程中更多旋转精度动态特征。传统的圆柱滚子轴承径向跳动测量方法只能对装配后的成套轴承进行测量，获得轴承径向跳动、端面跳动等一个方向上的单一数值评价指标，并不能根据已知或给定轴承零件几何误差预测轴承在实际工作状态下内圈径向跳动及其历程。

中国专利文献CN 105241407 A《圆柱滚子轴承内圈径向跳动预测方法》公开了一种内圈径向跳动预测方法，虽然其公开了可以根据已知或给定的轴承零件几何误差预测轴承在装配好后的内圈径向跳动及其历程，但是该方法仅限于无载荷约束下的内圈径向跳动预测，而轴承在实际工作时是必然会承受外部径向载荷的，因此，急需一种能够对载荷约束下的轴承内圈径向跳动进行预测的方法。

技术实现要素：

本发明提供了载荷约束下圆柱滚子轴承内圈径向跳动预测方法，以解决现有的轴承内圈径向跳动预测方法不能预测已知或给定轴承内圈滚道、外圈滚道和滚子表面几何误差时轴承在载荷约束下内圈径向跳动及其历程的问题。

为解决上述技术问题，本发明的载荷约束下圆柱滚子轴承内圈径向跳动预测方法包括：

1)获取轴承参数，所述轴承参数包括滚子直径、滚子个数、内圈滚道直径、外圈滚道直径、内圈滚道尺寸误差和圆度误差、外圈滚道尺寸误差和圆度误差及滚子尺寸误差和圆度误差；

2)使内圈转动一个设定步长角度获得一个旋转角度，计算轴承内圈在该旋转角度下的内、外圈滚道及滚子轮廓极坐标方程；

3)根据内、外圈滚道及滚子轮廓极坐标方程，计算坐标系X轴下方每个滚子与外圈滚道接触时的滚子圆心坐标，所述坐标系是指以外圈圆心为原点，水平方向为X轴，垂直方向为Y轴，建立的直角坐标系；

4)在设定径向载荷作用下，计算轴承滚子及内外圈滚道均为理想圆时的内圈圆心坐标(X₀，Y₀)；

5)根据内圈圆心坐标(X₀，Y₀)及X轴下方每个滚子与外圈滚道接触时的滚子圆心坐标，分别计算X轴下方每个滚子表面到内圈滚道的最小距离，根据最小距离判断滚子是否与内圈滚道接触，对于与内圈滚道接触的滚子，获取该滚子与内圈滚道的接触点坐标；

6)根据滚子与内圈滚道的接触点坐标，获得内圈滚道受到的支反力方向及内圈滚道在X、Y两个方向上的力平衡方程；

7)求解步骤6)中的力平衡方程，获得内圈滚道新的圆心坐标(X₁、Y₁)；

8)判断X₀与X₁的差值及Y₀与Y₁的差值是否均小于第一收敛误差，若否，令X₀＝X₁，Y₀＝Y₁，转至步骤7)，否则，圆心坐标(X₁、Y₁)即为内圈在该旋转角度下的圆心坐标，从而获得转动一个设定步长角度下的内圈径向跳动值。

重复步骤2)～8)，直至内圈旋转一周，获得每个内圈旋转角度下的径向跳动值，最大径向跳动值与最小径向跳动值之差即为内圈在设定径向载荷作用下的内圈径向跳动。

步骤3)中轴承下方每个滚子与外圈滚道接触时的滚子圆心坐标的计算方法为：求取滚子表面与外圈滚道之间的最短距离，当该最短距离的绝对值小于第二收敛误差时，该滚子此时的圆心坐标就是与外圈滚道接触时的滚子圆心坐标；否则，使滚子沿径向移动，直至滚子表面与外圈滚道之间的最短距离的绝对值小于第二收敛误差，获得该滚子与外圈滚道接触时的滚子圆心坐标。

滚子表面与外圈滚道之间的最短距离的计算方法为：

计算滚子表面到外圈滚道轮廓的距离L₁，AB为当Δθ_e在设定范围[-arcsin(D_w/d_e),arcsin(D_w/d_e)]内变化时，使L₁最小的值，其中，

AO为外圈滚道上A点的轮廓半径，Oo_rj为外圈圆心O与滚子圆心o_rj的距离，Δθ_e为外圈滚道上A点与第j个滚子圆心在圆周方向上的夹角；θ_B为滚子表面B点的位置角，D_w为滚子理想圆直径；d_e为轴承外圈滚道直径，ΔD_j为第j个滚子直径尺寸误差；C_rjm为第j个滚子表面轮廓第m阶谐波幅值；为第j个滚子表面轮廓第m阶谐波初始相位角，γ₁为滚子自转角度。

滚子表面与内圈滚道之间的最短距离的计算方法为：

计算滚子表面到内圈滚道轮廓的距离L₂，EF为当Δθ_i在设定范围[-arcsin(D_w/d_i),arcsin(D_w/d_i)]内变化时，使L₂最小的值，其中，

Eo_i为内圈滚道上E点的轮廓半径，o_io_rj为内圈圆心o_i到第j个滚子圆心o_rj的距离；Δθ_i为内圈滚道上E点与第j个滚子圆心在圆周方向上的夹角，θ_F为滚子表面F点的位置角，D_w为滚子理想圆直径；d_i为轴承内圈滚道直径，ΔD_j为第j个滚子直径尺寸误差；C_rjm为第j个滚子表面轮廓第m阶谐波幅值；为第j个滚子表面轮廓第m阶谐波初始相位角，γ₁为滚子自转角度。

内圈滚道在X、Y两个方向上的力平衡方程为：

其中，K_i为接触变形常数，δ_ij为第j个滚子与内圈滚道接触点处的弹性变形量，θ_j'为内圈滚道与第j个滚子接触点处的法线与X正半轴夹角，F_x、F_y为轴承内圈在X、Y方向的受力，Z₀为与内圈滚道接触的滚子个数。

当滚子处于第三象限，且滚子表面上任一点B在Oo_rj直线上方时，θ_B＝φ_ej+β_j-π；

当滚子处于第三象限且滚子表面上任一点B在Oo_rj直线下方时，θ_B＝π-φ_ej+β_j；

当滚子处于第四象限且滚子表面上任一点B在Oo_rj直线上方时，θ_B＝β_j-π-φ_ej；

当滚子处于第四象限且滚子表面上任一点B在Oo_rj直线下方时，θ_B＝β_j-π+φ_ej；

其中，φ_ej＝arccos((Ao_rj²+Oo_rj²-AO²)/(2Ao_rj×Oo_rj))，β_j＝2π(j-1)/Z+α(1-D_w/d_m)/2，其中，Z为滚子个数，α为内圈转动的角度，d_m为节圆直径，Ao_rj为第j个滚子圆心o_rj到外圈滚道上A点的距离。

当滚子处于第三象限且滚子表面上任一点F在o_io_rj直线上方时，

当滚子处于第三象限且滚子表面上任一点F在o_io_rj直线下方时，

当滚子处于第四象限且滚子表面上任一点F在o_io_rj直线上方时，

当滚子处于第四象限且滚子表面上任一点F在o_io_rj直线下方时，

其中，φ_ij＝arccos((Eo_rj²+o_io_rj²-Eo_i²)/(2Eo_rj×o_io_rj))，X_i、Y_i为内圈圆心坐标，X_rj、Y_rj为第j个滚子的圆心坐标，Eo_rj为第j个滚子圆心o_rj到内圈滚道E点的距离。

本发明的有益效果：本发明的载荷约束下圆柱滚子轴承内圈径向跳动预测方法，能够根据已知或给定轴承零件几何误差预测轴承在载荷约束下内圈径向跳动及其历程，从而实现根据轴承零件精度等级预测装配后成品轴承在工作状态下的旋转精度，为轴承零件精度设计及预测提供理论依据，对研制高精度滚动轴承产品具有积极作用，并可用于指导生产。

附图说明

图1为本发明圆柱滚子轴承结构图；

图2为本发明滚子与外圈滚道几何关系图；

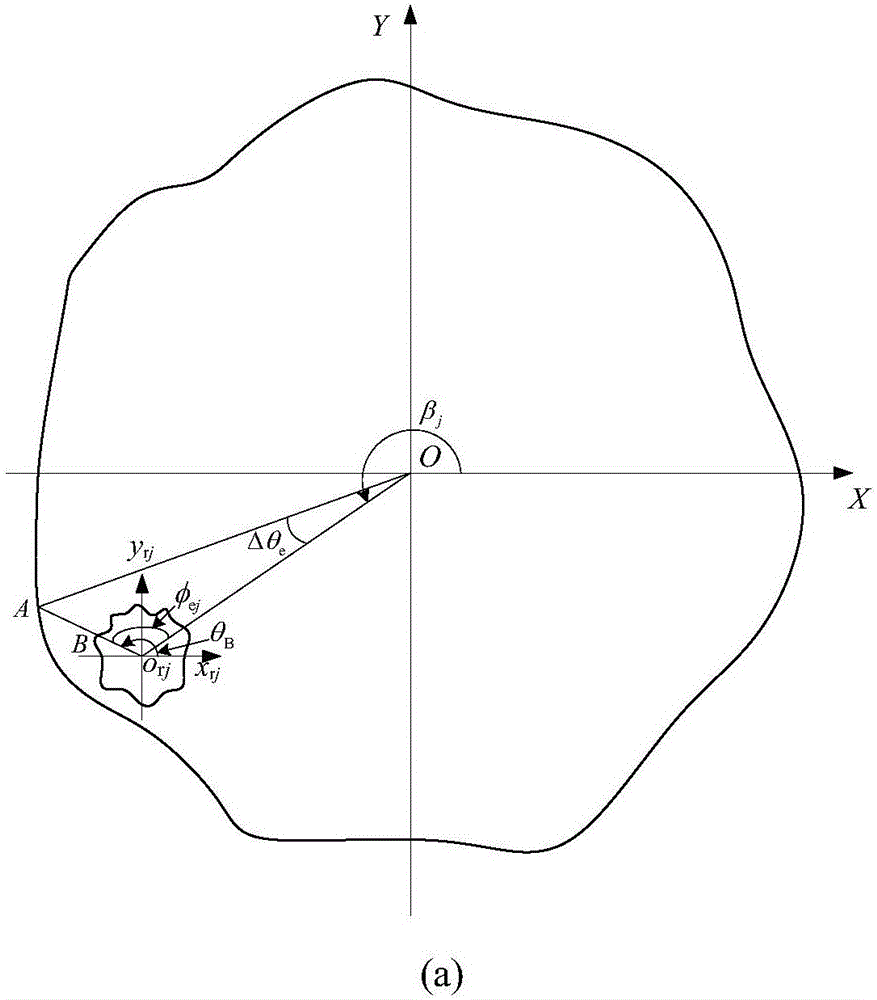
其中，图2(a)是本发明当滚子处于第三象限，且滚子表面上任一点B在Oo_rj直线上方时，滚子与外圈滚道的几何关系示意图；

图2(b)是本发明当滚子处于第三象限，且滚子表面上任一点B在Oo_rj直线下方时，滚子与外圈滚道的几何关系示意图；

图2(c)是本发明当滚子处于第四象限，且滚子表面上任一点B在Oo_rj直线上方时，滚子与外圈滚道的几何关系示意图；

图2(d)是本发明当滚子处于第四象限，且滚子表面上任一点B在Oo_rj直线下方时，滚子与外圈滚道的几何关系示意图；

图3为本发明滚子与内圈滚道几何关系图；

图3(a)是本发明当滚子处于第三象限，且滚子表面上任一点F在o_io_rj直线上方时，滚子与内圈滚道的几何关系示意图；

图3(b)是本发明当滚子处于第三象限，且滚子表面上任一点F在o_io_rj直线下方时，滚子与内圈滚道的几何关系示意图；

图3(c)是本发明当滚子处于第四象限，且滚子表面上任一点F在o_io_rj直线上方时，滚子与内圈滚道的几何关系示意图；

图3(d)是本发明当滚子处于第四象限，且滚子表面上任一点F在o_io_rj直线下方时，滚子与内圈滚道的几何关系示意图；

图4为本发明内圈滚道支反力方向示意图；

图5为本发明内圈滚道受力分析示意图；

图6为本发明滚子与套圈几何关系图；

图6(a)是本发明当滚子处于第三象限，且滚子表面上任一点D在o_io_rj直线上方时，滚子与内圈滚道的几何关系示意图；

图6(b)是本发明当滚子处于第三象限，且滚子表面上任一点D在o_io_rj直线下方时，滚子与内圈滚道的几何关系示意图；

图6(c)是本发明当滚子处于第四象限，且滚子表面上任一点D在o_io_rj直线上方时，滚子与内圈滚道的几何关系示意图；

图6(d)是本发明当滚子处于第四象限，且滚子表面上任一点D在o_io_rj直线下方时，滚子与内圈滚道的几何关系示意图；

图7为本发明内圈径向跳动历程图。

具体实施方式

下面结合附图，对本发明的技术方案作进一步详细说明。

轴承结构如图1所示，本发明中轴承内圈滚道、外圈滚道和滚子表面均有尺寸误差和形状误差，外圈固定，内圈旋转。本发明的轴承旋转精度预测方法基于以下假设：

(1)不考虑轴承零件轴向尺寸误差和圆度误差。

(2)不考虑保持器的影响，假设相邻滚子间夹角相等。

(3)不考虑滚子与套圈间相对滑动，即认为滚子与套圈间为纯滚动。

(4)不考虑轴承润滑对轴承旋转精度的影响。

本实施例的载荷约束下圆柱滚子轴承内圈径向跳动预测方法包括如下步骤：

1)获取轴承参数，所述轴承参数包括滚子直径、滚子个数、内圈滚道直径、外圈滚道直径、内圈滚道尺寸误差和圆度误差、外圈滚道尺寸误差和圆度误差及滚子尺寸误差和圆度误差；

2)使内圈转动一个设定步长角度获得一个旋转角度，计算轴承内圈在该旋转角度下的内、外圈滚道及滚子轮廓极坐标方程；

3)计算坐标系X轴下方每个滚子与外圈滚道接触时的滚子圆心坐标，所述坐标系是指以外圈圆心为原点，水平方向为X轴，垂直方向为Y轴，建立的直角坐标系；

4)在设定径向载荷作用下，采用静力学方法计算轴承滚子及内外圈均为理想圆时的内圈圆心坐标(X₀，Y₀)；

5)根据内圈圆心坐标(X₀，Y₀)及X轴下方每个滚子与外圈滚道接触时的滚子圆心坐标，分别计算X轴下方每个滚子表面到内圈滚道的最小距离，根据最小距离判断滚子是否与内圈滚道接触，对于与内圈滚道接触的滚子，获取该滚子与内圈滚道的接触点坐标；

6)根据滚子与内圈滚道的接触点坐标，获得内圈滚道受到的支反力方向及内圈滚道在X、Y两个方向上的力平衡方程；

7)求解步骤6)中的力平衡方程，获得内圈滚道新的圆心坐标(X₁、Y₁)；

8)判断X₀与X₁的差值及Y₀与Y₁的差值是否均小于第一收敛误差，若否，令X₀＝X₁，Y₀＝Y₁，转至第7步，否则，圆心坐标(X₁、Y₁)即为内圈在该旋转角度下的圆心坐标，从而获得转动一个设定步长角度下内圈在水平和竖直方向上的跳动位移，两者的矢量和即为内圈径向跳动值。

接着，重复步骤2)～8)，直至内圈旋转一周，获得每个内圈旋转角度下的径向跳动值，最大径向跳动值与最小径向跳动值之差即为内圈在设定径向载荷作用下的内圈径向跳动。

下面对上述实施例预测方法的各个步骤进行详细的阐述。

除了要获取步骤(1)中所述的轴承参数外，本实施例的方法中还必须设定轴承所承受的径向载荷力、内圈的转动步长角度、内圈的转动角度、第二收敛误差、第三收敛误差及第一收敛误差。

在步骤3)中要根据内、外圈滚道及滚子轮廓极坐标方程，来计算坐标系X轴下方(一般称为轴承下方)每个滚子与外圈滚道接触时的滚子圆心坐标，这里所述的坐标系是指以外圈圆心为原点，水平方向为X轴，垂直方向为Y轴，建立的直角坐标系；

而计算每个滚子与外圈滚道接触时的滚子圆心坐标时，首先要计算滚子表面到外圈滚道的最短距离，以下给出了一种计算滚子表面到外圈滚道的最短距离的具体方法：

假设轴承下方一个滚子由节圆直径处沿径向按设定的步长移动，直至与外圈滚道接触，从而获得此时滚子圆心到外圈圆心的距离，根据几何关系计算出滚子圆心坐标。为判断滚子与外圈滚道位置关系，提出了一种滚子表面到外圈滚道最短距离计算方法。

当内圈转动任意α角度时，第j个滚子移至某个位置时，滚子与外圈滚道几何关系如图2所示。由几何关系可知，外圈滚道上任一点A与滚子表面上任一点B的距离为：

AB＝Ao_rj-Bo_rj (1)

式中，Ao_rj为第j个滚子圆心o_rj到外圈滚道上A点的距离，由式(2)计算；Bo_rj为第j个滚子自转γ₁角度时B点的轮廓半径，由式(3)计算。

式中，AO为外圈滚道A点的轮廓半径，由式(4)计算；Oo_rj为给定的外圈圆心O到第j个滚子圆心o_rj的距离；Δθ_e为外圈滚道上A点与第j个滚子圆心在圆周方向上的夹角，-arcsin(D_w/d_e)≤Δθ_e≤arcsin(D_w/d_e)，其中，d_e为轴承外圈滚道直径；D_w为滚子理想圆直径。

式中，θ_A为外圈滚道上A点的位置角；γ₁为滚子自转角度，α为内圈转动的角度；Δd_e和ΔD_j分别为外圈滚道和第j个滚子的直径尺寸误差；C_em和C_rjm分别为外圈滚道和第j个滚子表面轮廓第m阶谐波幅值；和分别为外圈滚道和第j个滚子表面轮廓第m阶谐波初始相位角；θ_B为滚子表面B点的位置角，与滚子和B点所处位置有关：

当滚子处于第三象限，且滚子表面上任一点B在Oo_rj直线上方时，滚子与外圈滚道的几何关系如图2(a)所示，此时B点的位置角为θ_B＝φ_ej+β_j-π，其中，φ_ej＝arccos((Ao_rj²+Oo_rj²-AO²)/(2Ao_rj×Oo_rj))，β_j为第j个滚子的位置角，β_j＝2π(j-1)/Z+α(1-D_w/d_m)/2，其中，Z为滚子个数，α为内圈转动的角度，d_m为节圆直径；

当滚子处于第三象限，且滚子表面上任一点B在Oo_rj直线下方时，滚子与外圈滚道的几何关系如图2(b)所示，此时B点的位置角为θ_B＝π-φ_ej+β_j；

当滚子处于第四象限，且滚子表面上任一点B在Oo_rj直线上方时，滚子与外圈滚道的几何关系如图2(c)所示，此时B点的位置角为θ_B＝β_j-π-φ_ej；

当滚子处于第四象限，且滚子表面上任一点B在Oo_rj直线下方时，滚子与外圈滚道的几何关系如图2(d)所示，此时B点的位置角为θ_B＝β_j-π+φ_ej。

在式(1)中，当Δθ_e在一定范围内变化时，在外圈滚道上存在一个A点，滚子表面上存在一个B点，使A点到B点的距离AB最短，即为滚子表面到外圈滚道的最短距离。

当滚子表面到外圈滚道的最短距离大于第二收敛误差时，则认为滚子与外圈滚道接触未接触，继续径向移动滚子；当最短距离绝对值小于第二收敛误差时，则认为滚子与外圈滚道接触接触，从而获得此时滚子圆心到外圈圆心的距离，通过此距离计算出滚子的圆心坐标，如式(5)所示。以此类推，计算出每个滚子与外圈滚道接触时的圆心坐标。

步骤5)中内圈滚道的圆心坐标已知为(X₀，Y₀)，位于X轴下方每个滚子与外圈滚道接触时的滚子圆心坐标也获知，那么结合内、外圈滚道及滚子轮廓极坐标方程，就可以获知每个滚子表面与内圈滚道的最短距离，然后将每个最短距离的绝对值与第三收敛误差进行比较，就可以获知每个滚子是否与内圈滚道接触，对于接触的滚子，获取其与内圈滚道的接触点坐标，每个滚子表面与内圈滚道的最短距离的计算方法如下：

当内圈处于某位置时，滚子与内圈滚道的几何关系如图3所示。内圈滚道上任一点E与滚子表面上任一点F的距离为：

EF＝Eo_rj-Fo_rj (6)

式中，Eo_rj为第j个滚子圆心o_rj到内圈滚道E点的距离，由式(7)计算获得；Fo_rj为第j个滚子自转γ_r角度后F点的轮廓半径，由式(8)计算获得。

式中，Eo_i为内圈滚道上E点的轮廓半径，由式(9)计算获得；o_io_rj为内圈圆心o_i到第j个滚子圆心o_rj的距离；Δθ_i为内圈滚道上E点与第j个滚子圆心在圆周方向上的夹角，-arcsin(D_w/d_i)≤Δθ_i≤arcsin(D_w/d_i)。

式中，θ_E为内圈滚道上E点的位置角。θ_F为滚子表面F点的位置角，与滚子所处象限及F点的位置有关：

当滚子处于第三象限，且滚子表面上任一点F在o_io_rj直线上方时，滚子与内圈滚道的几何关系如图3(a)所示，其中，φ_ij＝arccos((Eo_rj²+o_io_rj²-Eo_i²)/(2Eo_rj×o_io_rj))，X_i、Y_i为内圈圆心坐标；

当滚子处于第三象限，且滚子表面上任一点F在o_io_rj直线下方时，滚子与内圈滚道的几何关系如图3(b)所示，

当滚子处于第四象限，且滚子表面上任一点F在o_io_rj直线上方时，滚子与内圈滚道的几何关系如图3(c)所示，

当滚子处于第四象限，且滚子表面上任一点F在o_io_rj直线下方时，滚子与内圈滚道的几何关系如图3(d)所示，

在式(6)中，当Δθ_i在一定范围内变化时，在内圈滚道上存在一个E点，滚子表面上存在一个F点，使EF的值最小。当EF的最小值大于第三收敛误差时，滚子与内圈滚道不接触；当EF的最小值的绝对值小于第三收敛误差时，滚子与内圈滚道接触。同时，可获得最小的EF值所对应的E点位置，即为滚子与内滚道最先接触的点，从而获得滚子与内圈滚道的接触点坐标。

步骤6)在获得了滚子与内圈滚道的接触点坐标后，要计算接触点处的法线方向，从而得到内圈滚道在此接触点处的支反力方向。

已知第j个滚子与内圈滚道接触点为G，如图4所示。则内圈滚道上任意一点的直角坐标表达式为：

式中，X、Y为内圈滚道上任意一点的坐标；R_i(θ)为内圈滚道轮廓半径极坐标方程，其中，θ为内圈滚道上任意一点的位置角；X_i、Y_i为内圈的圆心坐标。

内圈滚道上任意一点处的切线斜率表达式如式(11)所示，由几何关系可以推导出内圈任意一点处法线方向的斜率表达式，如式(12)所示。

由几何关系可知可推导出第j个滚子与内圈滚道上任意一点处法线方向与x_i正半轴夹角，如式(13)所示。

已知内圈滚道上任意一点G的坐标如式(14)所示，代入式(12)～(13)中，可获得内圈滚道上G点处的法线方向与x_i正半轴夹角，从而获得第j个滚子与内圈滚道接触点G处的支反力F_j的方向。

在得到内圈滚道受到的支反力方向后，可列出内圈在X、Y两个方向上的非线性力平衡方程，具体过程如下：

以轴承内圈为研究对象，对其进行受力分析。已知轴承内圈受外力F_x、F_y的联合作用，内圈滚道受到滚子作用的支反力为F₁、F₂、…、F_j，如图5所示。

第j个滚子与内圈滚道接触点处的弹性变形量可表示为：

δ_ij＝(X_icos(θ_j')+Y_isin(θ_j')-u_j)/2 (15)

式中，θ_j'为内圈滚道与第j个滚子接触点处的法线与X正半轴夹角；u_j为第j个滚子与内圈滚道径向最小游隙。

第j个滚子与内圈滚道接触点处的支反力，由Hertz接触弹性接触理论，可知:

式中，K_i为接触变形常数，K_i＝0.71*l^8/9/η，对于钢制滚子和滚道接触，K_i＝7.86×10⁴l^8/9，其中，l为滚子有效长度，η为等效弹性模量。

内圈力平衡方程如下：

其中，Z₀为与内圈接触的滚子个数。采用牛顿法求解式(17)和(18)为非线性方程组，获得内圈位移X_i和Y_i。

在获取内圈力平衡方程时，涉及到滚子与内圈滚道径向最小游隙，下面给出一种滚子与内圈滚道径向最小游隙的求解方法：

已知轴承下方滚子与外圈滚道接触，轴承内圈中心与轴承外圈中心重合，如图3所示。为获得此状态下内圈滚道与每个滚子表面的径向最小游隙，提出了一种内圈滚道与每个滚子表面的径向游隙计算方法。

内圈滚道、滚子和外圈滚道的几何关系如图6所示。内圈滚道上任一点C与滚子表面上任一点D的距离为：

CD＝Co_rj-Do_rj (19)

式中，Co_rj为第j个滚子圆心到内圈滚道C点的距离，由式(20)计算获得；Do_rj为第j个滚子自转γ₁角度后D点的轮廓半径，由式(21)计算获得。

式中，Co_i为内圈滚道上C点的轮廓半径，由式(22)计算获得；o_io_rj为内圈圆心到第j个滚子圆心的距离；Δθ_i为内圈滚道上C点与第j个滚子圆心在圆周方向上的夹角，-arcsin(D_w/d_i)≤Δθ_i≤arcsin(D_w/d_i)。

式中，θ_C为内圈滚道上C点的位置角；Δd_i为内圈滚道直径尺寸误差；C_im为内圈滚道和第j个滚子表面轮廓第m阶谐波幅值；为内圈滚道第m阶谐波初始相位角；θ_D为滚子表面D点的位置角，与滚子所处象限及D点的位置有关。

当滚子处于第三象限，且滚子表面上任一点D在o_io_rj直线上方时，滚子与内圈滚道的几何关系如图6(a)所示，θ_D＝β_j-π+ψ_ij，其中，ψ_ij＝arccos((Co_rj²+o_io_rj²-Co_i²)/(2Co_rj×o_io_rj))；

当滚子处于第三象限，且滚子表面上任一点D在o_io_rj直线下方时，滚子与内圈滚道的几何关系如图6(b)所示，θ_D＝β_j+π-ψ_ij；

当滚子处于第四象限，且滚子表面上任一点D在o_io_rj直线上方时，滚子与内圈滚道的几何关系如图6(c)所示，θ_D＝β_j-π-ψ_ij；

当滚子处于第四象限，且滚子表面上任一点D在o_io_rj直线下方时，滚子与内圈滚道的几何关系如图6(d)所示，θ_D＝β_j-π+ψ_ij。

在式(19)中，当Δθ_i在一定范围内变化时，在内圈滚道上存在一个C点，滚子表面上存在一个D点，使C点到D点的距离CD最小，即为第j个滚子表面到内圈滚道的最小游隙。同理，可获得轴承下方每个滚子与内圈滚道的最小游隙u_j。

下面举例说明上述的预测方法：

第1步，给定轴承参数：外圈滚道直径d_e为75.032mm，内圈滚道直径d_i为54.991mm，滚子直径D_w为10mm，滚子个数Z为14，滚子有效长度l为9.6mm。内圈滚道尺寸误差为0.0006mm,外圈滚道尺寸误差为0.001mm，每个滚子尺寸误差均为0.0004mm；内圈滚道圆度误差ΔR_i＝0.0005cos(8θ_i),外圈滚道圆度误差ΔR_e＝0.0007cos(7θ_e)，每个滚子圆度误差ΔR_r＝0.0002cos(4θ_r)；

设定内圈转动步长角度为1度，内圈的转动角度为360度，轴承受到径向载荷F_r为4450N，将第一、二、三收敛误差均设为0.00001，当然，第一、二、三收敛误差也可设置为不同的值。

第2步，内圈转动1度；

第3步，计算内圈滚道轮廓半径极坐标方程R_i(θ_i)＝24.748+0.0003+0.0005cos(8(θ_i-0.0174))、外圈滚道轮廓半径极坐标方程R_e(θ_e)＝35.7705+0.0005+0.0007cos(7θ_e)及第j个滚子轮廓半径极坐标方程R_rj(θ_rj)＝5.5+0.0002+0.0002cos(4(θ_rj-0.0074))；

第4步，根据上述计算出来的各轮廓半径极坐标方程及滚子圆心坐标计算方法，获得轴承下方每个滚子与外圈滚道接触时的滚子圆心坐标；

第5步，轴承下方每个滚子与外圈滚道接触，此时假设轴承内圈与外圈同心，根据滚子表面与内圈滚道最小游隙计算方法，分别获得轴承下方每个滚子表面与内圈滚道间的最小游隙值。

第6步，计算在设定的径向载荷作用下轴承零件无几何误差时内圈位移X₀、Y₀(内圈的圆心坐标)，X₀≈0，Y₀＝-3.83×10^-5(5F_r/Z)^0.9/l^0.8-(d_e-d_i-2D_w)/2＝-0.0253mm，将其设置为内圈的初始位置坐标；

第7步，已知轴承内圈圆心坐标为(X₀,Y₀)，根据滚子表面到内圈滚道的最小距离计算方法，分别获得轴承下方每个滚子表面到内圈滚道的最小距离，若最小距离的绝对值小于第三收敛误差，则滚子与内圈滚道接触，获得滚子表面与内圈滚道的接触点坐标；

第8步，已知滚子与内圈滚道的接触点坐标，根据内圈滚道支反力方向计算方法，获得每个接触滚子对内圈滚道作用的支反力方向，从而列出内圈在X、Y两个方向上的力平衡方程；

第9步，用牛顿法求解非线性力平衡方程，获得内圈新的位置坐标(X₁,Y₁)，其中，X₁＝-0.00161，Y₁＝-0.0358；

第10步，判断X₀与X₁、Y₀与Y₁差值的绝对值是否均小于第一收敛误差ε，|X₀-X₁|＝0.00161>ε，|Y₀-Y₁|＝0.0105>ε，不满足收敛条件，X₀＝X₁，Y₀＝Y₁，转至第7步，重复计算第7～10步，如果满足收敛条件，则X₁、Y₁即为内圈在一个转动步长角度下的圆心坐标，从而获得在一个转动步长角度下内圈径向跳动值；

第11步，以此类推，内圈继续转动一个步长，重复第3～10步，内圈旋转一周即360度，获得每个内圈转动步长角度下的径向跳动值，如图7所示，其最大径向跳动值为0.032229mm，最小径向跳动值为0.031682mm，在此载荷作用下内圈径向跳动为0.032229mm-0.031682mm＝0.000547mm。