一种使用高频地下水位数据自动求取含水层参数的方法与流程

本发明涉及水资源评估技术领域，具体涉及一种使用高频地下水位数据自动求取含水层参数的方法。

背景技术：

地下水作为地球水循环的重要一环，是人类重要的水储存资源之一。一直到20世纪70年代，我国面临的地下水问题主要由单纯的安全性需求(如饮水和灌溉)驱动。但80年代之后中国的超高速发展在成为世界经济发展奇迹的同时，也带来了许多严重的地下水环境和资源问题，如南方地下水水质恶化，北方平原地区地下水由于大量开采使用导致的地下水水位下降等。

传统的地下水水流方向为沿含水层水平方向为主，随着农业、工业和生活用水需求的增加，抽水井数量逐年增加，导致地下水尤其是平原区的地下水流场基本脱离天然状态，常常由垂向水量交换主导，而不再是地下水径流过程主导。反映在地下水数值模型中为流量的消长不再受水头边界的控制，而受垂向补径排过程，如抽水、农业灌溉、降雨等控制。

然而，在建立地下水瞬时流模型时，与垂向补径排过程息息相关的入渗系数、给水度和外部应力(抽水量)等模型参数却较难获得，虽然一部分可通过试验和调查获得，但由于地层异质性和数据资料的准确程度，更多情况下使用经验参数值进行赋值，并且缺乏校正的依据，从而增加了水文驱动因子刻画的难度。

当前，我国局部试点地区已具备高频率高密度地下水监测数据，全国的高频监测网也正在施工，由此获得的高频率高密度水位监测数据是极佳的地下水系统信息来源，但目前未得到充分利用。因此，我们充分利用高密高频水位和降水量监测数据，通过设计合理的求参方法，求取以垂直方向补径排为主的地下水瞬时流模型中潜水入渗系数、给水度、以及净开采强度等关键水文地质参数的时空分布，并且实时同化更新至地下水模型，为全国地下水信息系统构建、地下水大数据挖掘、地下水资源优化管理与合理配置提供精准数据支撑。

现有求取地下水模型潜水参数的方法有：

1)Water Table Fluctuation(WTF)方法：

使用公式R＝S×ΔH，其中R为含水层水量变化，S为给水度，ΔH为水位变化。该方法的缺点是未考虑灌溉或其它垂向方向可能导致水位升降的水力因素，比较粗放简单。

2)Episodic Master Recession(EMR)方法：

此方法基于WTF方法，使用降雨阈值进行参数求取，对于次雨的刻画更为细腻，但无法处理大规模抽水开采造成的扰动，也无法精确刻画给水度S。

技术实现要素：

本发明的目的是针对现有技术中的不足，提供一种使用高频地下水位数据自动求取含水层参数的方法，为全国地下水信息系统构建、地下水大数据挖掘、地下水资源优化管理与合理配置提供精准数据支撑。

为实现上述目的，本发明公开了如下技术方案：

一种使用高频地下水位数据自动求取含水层参数的方法，包括如下步骤：

S1 基本条件假设：假设地下水位的波动由入渗补给过程和净开采过程决定；含水层水分运移由垂向地下水水文循环为主导；且含水层补给量与降水量成正比；

S2 地下水水位及降水数据预处理：收集国家地下水监测网中多年长序列高频高密水位监测数据，绘制地下水水位变化线，并将水位线进行平滑处理；收集研究区内气象监测点多年高频高密降水数据，并根据气象监测站点的空间分布特征进行分区，将降水量分配至区域内的水位监测点，并与水位监测数据进行时间匹配，形成日降水量与水位时间序列；

S3 正向模拟求取水位及降水量：根据地下水储水量与垂向补给和净开采量之间的关系，设置入渗系数α、年度总净开采模数NDT、净开采模数月分配系数βi，其中i＝1,2……12，和含水层给水度Sy，共15个参数正向模拟地下水瞬时水位和降水量；

S4 系统优化计算：根据设置的15个参数与地下水瞬时水位和区间累计降水量间的关系，设置15个参数的初始值，使用系统优化计算的方法，即Levenberg-Marquardt算法，根据瞬时水位和降水量的计算值与观测值的差值，反复更新参数取值，计算获得区间累计降水量、瞬时水位数据与多年高频高密降水数据、水位监测数据误差最小时，15个给定地下水模型参数的最优估算值；

S5 数据修正：通过上述步骤求取参数的方法假设目的含水层地下水水文过程主要为垂向循环，当考虑水平向循环对地下水位变化的影响时，需要使用地下水侧向径流或越流数据与参数自动求取过程进行迭代，对求取的参数进行修正，消除水平向水文循环对水位变化的影响；

S6 模型校验：通过上述步骤计算求得年际尺度地下水瞬时流模型参数值，为保证参数计算的准确性，再利用传统的地下水模型与含水层属性资料对这些参数进行校验，其中，参数包括入渗系数α、年度总净开采模数NDT、净开采模数月分配系数βi，其中i＝1,2……12，和含水层给水度Sy。

进一步的，所述步骤S2中，绘制水位变化线时，以时间为横坐标、含水层瞬时水位为纵坐标，绘制水位变化线；并使用数据平滑方法对地下水水位线平滑化，其中数据平滑方法包括但不限于移动平均值法、移动窗口拟合多项式平滑法或移动窗口加权平滑法。

进一步的，所述步骤S2中，根据气象监测站点的空间分布特征进行分区时，兼顾地形因素与降水观测点的分布进行分区，将不同站点的降水观测数据进行空间插值后分配给相邻地下水水位监测站点。

进一步的，所述步骤S3中，求取地下水瞬时水位具体方法如下：对于满足前提假设的含水层单元，即单位面积地下潜水含水层的水量V受垂向补给和排泄过程的影响发生变化，多种补给和排泄途径分别归纳为地下水净补给量和净开采量，公式表达如下：

ΔV＝NR-ND (1)

上式中ΔV表示单位面积含水层在指定时间段内的水量变化，单位为m；NR表示单位面积含水层在指定时间段内接受的地下水净补给量，单位为m；ND表示地下水净开采模数，表示单位面积含水层在指定时间段内的地下水净开采量，单位为m；

ΔV＝ΔH×Sy (2)

NR＝IFp+IFr+RFup≈P×α (3)

ND＝Ua+Um+ET+RFdown (4)

上式中，ΔH表示某时间段内含水层水位变化，单位为m；Sy表示给水度，无量纲；NR表示单位面积地下水净补给量，单位为m；IFp和IFr分别表示降水和河流等地表水体对地下水的垂向补给，RFup表示其他含水层对该含水层的越流补给；P为降水量，单位为m；α表示入渗系数，无量纲；ND表示地下水净开采模数，单位为m；Ua和Um分别表示农业开采用水和市政开采用水，ET表示地下水通过蒸散发途径的排泄量，RFdown表示含水层对其他含水层的越流排泄；

NR反映了所有潜在对水位波动产生影响的入渗补给来源对目标含水层水量增加的贡献，净补给量NR简化为降水量与入渗系数的乘积，此处入渗系数为综合入渗系数；净开采模数ND反应了所有潜在对水位波动产生影响的排泄途径对目标含水层水量减少的贡献；

地下水水位波动的变化值ΔH通过上述数据处理过程获得的日地下水位时间序列获得，根据公式(1)至(4)可得：

H＝H0+ΔH＝H0+ΔV/Sy＝H0+(P×α-ND)/Sy (5)

其中H0是某时间段开始时地下水的瞬时水位，H为某时间段任一时刻地下水瞬时水位；

由于组成净开采模数ND的水文过程多数具有季节变化特征，特别是在平原区占净开采模数主要份额的农业开采量Ua有着明显的季节差异，因此，为体现净开采模数的年内变化特征，通过净开采模数月分配系数βi，其中i＝1,2……12，将年度总净开采模数NDT分配至12个月中，表示为ND1，ND2……ND12，因此，依据式(5)所列关系，使用降水量P，入渗系数α，年度总净开采模数NDT、净开采模数月分配系数βi和含水层给水度Sy模拟含水层的瞬时水位；

求取区间累计降水量具体方法如下：地下水水位随时间发生起伏变化，而具有相同水位不同时间点间含水层水位未发生变化，即ΔH＝0，根据公式(5)可得此时间区间p之间：

P＝NDp/α (6)

P为该时段内某地下水位观测点代表范围内的降水量；NDp为该时间段内净开采模数，根据参数年度总净开采模数NDT与净开采模数月分配系数βi计算获得；α为含水层入渗系数；选取数对具有相同水位的时间点，所选时间段内地下水净补给等于净开采量，根据公式(6)，用入渗系数α，年度总净开采模数NDT、净开采模数月分配系数βi来模拟求取降水量P。

进一步的，所述步骤S4中，进行系统优化计算的具体步骤如下：联立地下水瞬时水位求取公式(5)和降水量求取公式(6)，其中入渗系数α、年度总净开采模数NDT、净开采模数月分配系数βi和含水层给水度Sy为参数x，瞬时水位H和区间累计降水量P为模拟值y，与模拟值相对应的观测值即为地下水水位实际监测数据和降水量实际观测数据；

系统优化算法使用的是Levenberg-Marquardt算法，主要通过逐步迭代不断逼近求解目标函数最小值，是一种应用广泛的非线性最小二乘优化算法，目标函数则是计算所得模拟值与实际观测值的差异函数，而计算的模拟值则依赖于参数的取值；

本方法中，基于公式(5)与(6)，参数α、NDT、βi和Sy存储在矩阵x中，而模拟地下水瞬时水位H和降水量P在矩阵y中，x与y的关系可用下式表示：

y＝M(x) (7)

x为有n个元素的矩阵，n表示参数个数，y为m个元素的矩阵，m表示模拟值个数，M是一个非线性函数，将模型参数与模拟值关联起来，将式(7)线性化可得

其中和分别是上一次迭代中参数和模拟值的矩阵，J为m行n列的雅各比偏导数矩阵；

i,j分别是矩阵J的行列数，在计算过程中，矩阵循环更新，每次循环加入增量矩阵u：

其中k为循环次数，上标“-”表示矩阵更新前的计算值，“+”表示更新后的计算值，T为转置符号，O为m行m列的观测值权重矩阵；

经过转换，得到最终的目标函数Φ如下：

设置初始参数矩阵得模拟结果矩阵通过观测值矩阵y，使用一阶泰勒展开式对J求解，通过公式(10)与(11)计算参数增量矩阵和更新的矩阵并将其存入参数矩阵中，进行下一步的循环计算；通过不断计算x中参数的取值，即最终使得目标函数Φ最小；

上述基于公式(5)与(6)的逆向调参过程同时进行，通过反复调整计算入渗系数α、年度总净开采模数NDT、净开采模数月分配系数βi和含水层给水度Sy的取值，使得区间累计降水量计算值与区间累计降雨量观测值P、瞬时水位计算值与地下水位自动监测数据H的差异最小，最终获得15个参数的最优估算值。

进一步的，所述步骤S5中，迭代过程中的操作包括：

(1)根据基础退水过程的拟合迭代：基础退水过程表示在没有垂向补给与排泄条件下，区域内水位变化情况，主要由外部水平向边界控制，采用无降雨和开采条件下的地下水模型拟合所得，以消除含水层水平向由主要外部边界条件控制引起的水位变化的影响；

(2)根据边界退水过程的拟合迭代：边界退水表示由特定水力边界引发的局部侧向径流，采用计算河流、湖泊的特定水力边界对研究区域的地下水补给量得到，以消除特定水力边界引发的局部侧向径流对潜水水位的影响；

(3)根据差异退水过程的拟合迭代：差异退水表示由参数差异引发的局部侧向径流，采用观测计算两区域边界处的水流量得到，以消除参数差异引发的局部侧向径流的影响；

(4)根据越流过程的拟合迭代：越流过程表示下部承压水的顶托补给，与基础退水合并考虑，以消除承压水对含水层的垂向补给的影响。

进一步的，还包括S6模型校验步骤，模型的具体的校验内容如下：

S6.1 将参数进行空间插值，并作为模型参数代入传统水流模型中，将水流模型运行结果与实际水位、水量监测数据进行比对，对这15个参数进行同化和校验；

S6.2 对于每个地下水位监测点，均求取一套模型参数，使用区域平均水位和平均降水量求取15个参数作为参考，对单点求取的参数进行校验；

S6.3 对于部分参数，使用土地利用类型分区等面状信息估算参数的取值范围，对参数进行校验；

S6.4 对于有较为精确的局部含水层属性的地下水观测点，使用局部含水层属性参数对该地下水位监测点求取的参数进行校验。

本发明公开的一种使用高频地下水位数据自动求取含水层参数的方法，具有以下有益效果：

本方法充分考虑了当前平原地区地下水以垂向水文循环为主导的特征，创建了利用大数据获取含水层重要参数的计算方法。利用长序高频高密地下水水位和降水量监测数据，根据入渗系数、净开采模数、给水度与降水量、水位变化之间的关系，应用系统优化算法，求取15个重要的，以垂向水文循环为主导的地下水含水系统参数值。并使用地下水含水层的基础边界条件、特征水力边界条件等局部侧向径流与越流过程对求取的参数进行拟合迭代修正，利用传统地下水模型与含水层属性资料对这些参数进行校验。

可实时将上述参数更新至地下水数值模型，充分发挥地下水模型的运算能力，为地下水资源优化利用和合理配置提供高效精确的技术支撑。

附图说明

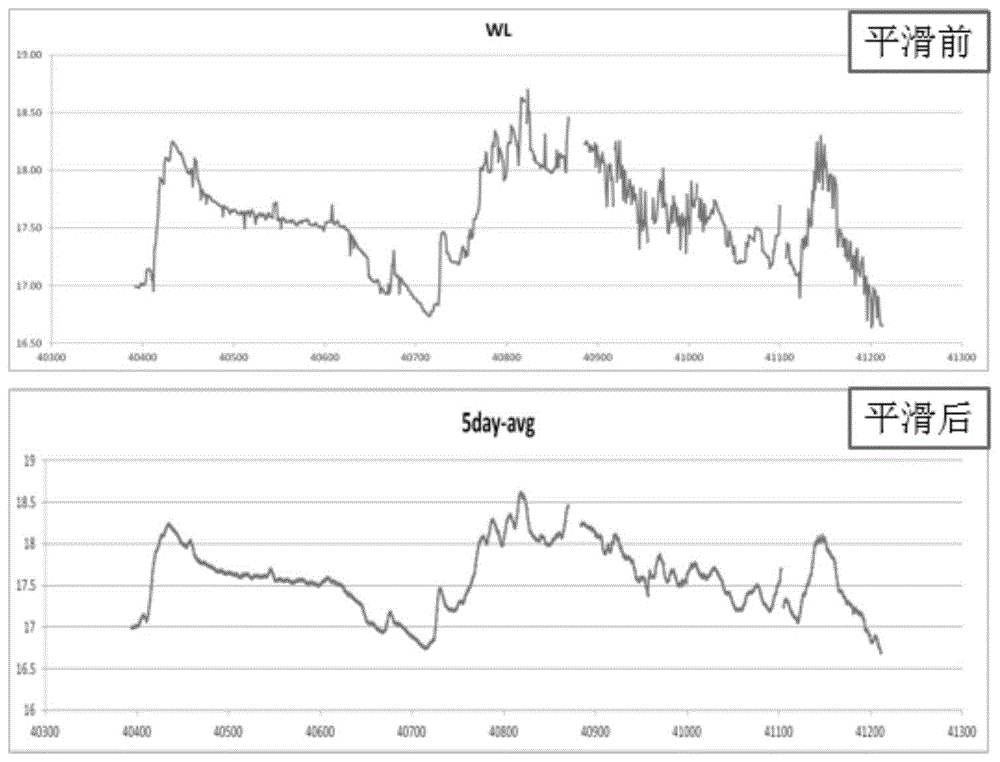
图1是本发明地下水瞬时水位线平滑化的前后对比图。

具体实施方式

下面将对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。

本发明的核心是提供一种使用高频地下水位数据自动求取含水层参数的方法，为地下水资源优化利用和合理配置提供高效精确的技术支撑。

本方法以垂向水文循环为主导的地下水含水系统为主要研究对象，使用长序列高频高密地下水水位监测数据和长序列高频高密(逐日)降水数据。假定水位波动时间序列中，相同水位时间段间的入渗量(降水量×入渗系数)等于净开采模数，研究区内入渗系数为常数，并且，水位波动的外部驱动力以一个水文年为周期，净开采模数的时间变化以月度为分辨率。设入渗系数、给水度、地下水年度总净开采模数、净开采模数月分配系数(12个月)这15个待求取参数；联立方程确定各等水位时间区段累计降水量、地下水瞬时水位与入渗系数、给水度、净开采模数之间的关系；使用系统优化算法，求取令计算所得降水量与观测值、计算所得长序水位时间序列与观测数据误差最小时，15个给定参数的最优估算值。通过考虑基础退水、边界退水等地下水侧向径流或越流过程对地下水水位变化的影响，对上述参数进行迭代修正。为保证计算所得参数的精度，将其代入传统地下水数值模型中，通过比对模型所得区域平均参数、利用地下水点面信息资料等方法对上述过程求取的参数进行校验。具体如下：

一种使用高频地下水位数据自动求取含水层参数的方法，包括如下步骤：

S1 基本条件假设：本方法主要应用于受地下水位垂向补径排过程影响的含水层，如平原区潜水含水层。平原地区潜水位的升降主要受含水层垂向水力循环过程，如降水入渗、农业灌溉用水开采及回灌、市政用水开采的影响，而非传统意义上的水平方向水文循环为主导。

假设地下水位的波动由入渗补给过程和净开采过程决定；含水层水分运移由垂向地下水水文循环为主导；且含水层补给量与其主要驱动因子(即降水量)成正比；

S2 地下水水位及降水数据预处理：收集国家地下水监测网中多年长序列高频高密水位监测数据，绘制地下水水位变化线，并将水位线进行平滑处理；收集研究区内气象监测点多年高频高密(逐日)降水数据，并根据气象监测站点的空间分布特征进行分区，将降水量分配至区域内的水位监测点，并与水位监测数据进行时间匹配，形成日降水量与水位时间序列；

绘制水位变化线时，以时间为横坐标，含水层瞬时水位为纵坐标，绘制水位变化线。含水层水位受多种补给径流和排泄过程影响，高频高密数据日间波动较大，因此需要将收集的地下水水位线平滑化，便于数据的进一步分析。常用的数据平滑化方法有移动平均值法、移动窗口拟合多项式平滑法、移动窗口加权平滑法(Kerne l法)等。水位线平滑前后的水位线变化如图1所示。

对研究区域内不同站点降水量观测数据进行空间分区，与地下水水位观测数据进行匹配时，需兼顾地形因素与降水观测站点的分布进行分区，必要时将不同站点的降水观测数据进行空间插值后分配给相邻地下水水位监测站点。

S3 正向模拟求取水位及降水量：根据地下水储水量与垂向补给和净开采量之间的关系，设置入渗系数α、年度总净开采模数NDT、净开采模数月分配系数βi，其中i＝1,2……12，和含水层给水度Sy，共15个参数正向模拟地下水瞬时水位对降水量的响应关系；

求取地下水瞬时水位具体方法如下：对于满足前提假设的含水层单元，即地下潜水含水层的储水量V受垂向补给和排泄过程的影响发生变化，多种补给和排泄途径分别归纳为地下水净补给和净开采量，公式表达如下：

ΔV＝NR-ND (1)

上式中ΔV表示单位面积含水层在指定时间段内的水量变化，m；NR表示单位面积含水层在指定时间段内接受的地下水净补给量，m；ND为地下水净开采模数，表示单位面积含水层在指定时间段内的地下水净开采量，m；

ΔV＝ΔH×Sy (2)

NR＝IFp+IFr+RFup≈P×α (3)

ND＝Ua+Um+ET+RFdown (4)

上式中，ΔH表示某时间段内含水层水位变化，m；Sy表示给水度，无量纲。NR表示单位面积地下水净补给量，单位为m，IFp和IFr分别表示降水和河流等地表水体对地下水的垂向补给，RFup表示其他含水层对该含水层的越流补给；P为降水量，m；α表示入渗系数，无量纲。ND表示地下水净开采模数，m，Ua和Um分别表示农业开采用水和市政开采用水，ET表示地下水通过蒸散发途径的排泄量，RFdown表示含水层对其他含水层的越流排泄；

NR反映了所有潜在对水位波动产生影响的入渗补给来源对目标含水层水量增加的贡献，净补给量NR简化为降水量与入渗系数的乘积，此处入渗系数为综合入渗系数。净开采模数ND反应了所有潜在对水位波动产生影响的排泄途径对目标含水层水量减少的贡献；

地下水水位波动的变化值ΔH通过上述数据处理过程获得的日地下水位时间序列获得，根据公式(1)至(4)可得：

H＝H0+ΔH＝H0+ΔV/Sy＝H0+(P×α-ND)/Sy (5)

其中H0是某时间段开始时地下水的瞬时水位，H为某时间段任一时刻地下水瞬时水位；

由于组成净开采模数ND的水文过程多数具有季节变化特征，特别是在平原区占净开采模数主要份额的农业开采量Ua有着明显的季节差异，因此，为体现净开采模数的年内变化特征，通过净开采模数月分配系数βi，其中i＝1,2……12，将年度总净开采模数NDT分配至12个月中，表示为ND1，ND2……ND12，因此，依据式(5)所列关系，使用降水量P，入渗系数α，年度总净开采模数NDT、净开采模数月分配系数βi和含水层给水度Sy模拟含水层的瞬时水位；

求取区间累计降水量具体方法如下：地下水水位随时间发生起伏变化，而具有相同水位的不同时间点间含水层水位未发生变化，即ΔH＝0，根据公式(5)可得此时间区间p之间：

P＝NDp/α (6)

P为该时段内某地下水位观测点代表范围内的降水量；NDp为该时间段内净开采模数，根据参数年度总净开采模数NDT与净开采模数月分配系数βi计算获得；α为含水层入渗系数；从图1中选取数对具有相同水位的时间点，所选时间段内地下水净补给等于净开采模数，根据公式(6)，可用入渗系数α，净开采总量NDT、净开采模数月分配系数βi来模拟求取降水量P。

S4系统优化计算：根据设置的15个参数与地下水瞬时水位和区间累计降水量间的关系，设置15个参数的初始值，使用系统优化计算的方法，即Levenberg-Marquardt算法，根据瞬时水位和降水量的计算值与观测值的差值，反复更新参数取值，计算获得区间累计降水量、瞬时水位数据与多年高频高密降水数据、水位监测数据误差最小时，15个给定地下水模型参数的最优估算值；

系统优化计算的具体步骤如下：联立地下水瞬时水位求取公式(5)和降水量求取公式(6)，其中入渗系数α、年度总净开采模数NDT、净开采模数月分配系数βi和含水层给水度Sy为参数x，瞬时水位H和区间累计降水量Pp为模拟值y。与模拟值相对应的观测值即为地下水水位实际监测数据和降水量实际观测数据。

系统优化算法使用的是Levenberg-Marquardt算法，主要通过逐步迭代不断逼近求解目标函数最小值，是一种应用广泛的非线性最小二乘优化算法，目标函数则是计算所得模拟值与实际观测值的差异函数，而计算的模拟值则依赖于参数的取值；

本方法中，基于公式(5)与(6)，参数α、NDT、βi和Sy存储在矩阵x中，而模拟地下水瞬时水位H和降水量P在矩阵y中，x与y的关系可用下式表示：

y＝M(x) (7)

x为有n个元素的矩阵，n表示参数个数，y为m个元素的矩阵，m表示模拟值个数，M是一个非线性函数，将模型参数与模拟值关联起来，将式(7)线性化可得

其中和分别是上一次迭代中参数和模拟值的矩阵，J为m行n列的雅各比偏导数矩阵；

i,j分别是矩阵J的行列数，在计算过程中，矩阵循环更新，每次循环加入增量矩阵u：

其中k为循环次数，上标“-”表示矩阵更新前的计算值，“+”表示更新后的计算值，T为转置符号，O为m行m列的观测值权重矩阵；

经过转换，得到最终的目标函数Φ如下：

设置初始参数矩阵得模拟结果矩阵通过观测值矩阵y，使用一阶泰勒展开式对J求解，通过公式(10)与(11)计算参数增量矩阵u0和更新的矩阵并将其存入参数矩阵中，进行下一步的循环计算；通过不断计算x中参数的取值，即最终使得目标函数Φ最小；

上述基于公式(5)与(6)的逆向调参过程同时进行，通过反复调整计算入渗系数α、年度总净开采模数NDT、净开采模数月分配系数βi和含水层给水度Sy的取值，使得区间累计降水量计算值与区间累计降雨量观测值P、瞬时水位计算值与地下水位自动监测数据H的差异最小，最终获得15个参数的最优估算值。

S5数据修正：通过上述步骤求取参数的方法假设目的含水层的地下水水文过程主要为垂向循环，当考虑水平向循环对地下水位变化的影响时，需要使用地下水侧向径流或越流数据与参数自动求取过程进行迭代，对求取的参数进行修正，消除水平向水文循环对水位变化的影响；

迭代过程中的操作包括：

(1)根据基础退水过程的拟合迭代：基础退水过程表示在没有垂向补给与排泄条件下，区域内水位变化情况，主要由外部水平向边界控制，如给定水头和给定流量边界条件。可采用无降雨和开采条件下的地下水模型拟合所得，以消除含水层水平向由主要外部边界条件控制引起的水位变化的影响；

(2)根据边界退水过程的拟合迭代：边界退水表示由特定水力边界引发的局部侧向径流，如区域的河流、湖泊等边界对研究区域地下水的水平补给与排泄产生的影响。多采用计算河流、湖泊的特定水力边界对研究区域的地下水补给量得到，以消除特定水力边界引发的局部侧向径流对潜水水位的影响；

(3)根据差异退水过程的拟合迭代：差异退水表示由参数差异引发的局部侧向径流，如建筑用地与相邻农田用地含水层的渗透系数不同，导致在两种渗透系数不同的区域边界处出现局部侧向径流。多采用观测计算两区域边界处的水流量得到，以消除参数差异引发的局部侧向径流的影响；

(4)根据越流过程的拟合迭代：越流过程表示下部承压水的顶托补给，常与基础退水合并考虑，以消除承压水对含水层的垂向补给的影响。

S6模型校验：通过上述步骤计算求得年际尺度地下水瞬时流模型参数值，为保证参数计算的准确性，再利用传统的地下水模型与含水层属性资料对这些参数进行校验，其中，参数包括入渗系数α、年度总净开采模数NDT、净开采模数月分配系数βi，其中i＝1,2……12，和含水层给水度Sy。

模型的具体的校验内容如下：

S6.1 将参数进行空间插值，并作为模型参数代入传统水流模型中，将水流模型运行结果与实际水位、水量监测数据进行比对，对这15个参数进行同化和校验；

S6.2 对于每个地下水位监测点(对应一套长序高频地下水水位与降水量时间序列)，均求取一套模型参数(15个)，使用区域平均水位和平均降水量求取15个参数作为参考，对单点求取的参数进行校验；

S6.3 对于部分参数，如入渗系数、净开采模数等，可以使用土地利用类型分区等面状信息进行估算，利用面状信息估算的参数取值范围，对参数进行校验；

S6.4 对于有较为精确的局部含水层属性(如岩性柱状图、局地抽水试验点等)的地下水观测点，可以使用局部含水层属性参数对该地下水位监测点求取的参数进行校验。

本发明的关键点在于：以垂向水文循环为主的含水层为研究对象，高效充分利用现有高频高密地下水监测数据。使用降水量与入渗系数简化净补给量；同时选择具有相同水位不同时间点的数据，假定该时间段内含水层净补给与净开采模数相等。根据高频高密降水量观测数据和高频高密地下水瞬时水位监测数据，采用系统优化算法求取入渗系数、年度总净开采模数、净开采模数月分配系数和给水度等地下水瞬时流模型参数。

本发明使用含水层的基础边界条件、特征水力边界条件等局部侧向径流与越流过程对求取的参数进行拟合迭代修正；利用传统的地下水数值模型与含水层属性资料对求取的参数进行校验。

通过对每个地下水位监测点的瞬时水位变化与降水量的计算值与观测值的拟合，均可求取一套参数(α，NDT，βi(i＝1～12)，Sy)，该套参数可用于一个观测点，也可以在研究区域中进行空间插值。在缺乏地下水参数的情况下，为地下水数值模拟提供了有力的定量输入条件支撑。

本发明求取了全国主要平原区潜水瞬时流模型中的主要参数(α，NDT，βi，Sy)，建立并维护全国首个统一的地下水模型；可补充完善国家基础地质调查内容，建立并维护全国平原区入渗系数、地下水净开采模数和浅层地下水给水度分区图。

本发明可用于开发地下水水流数值模型实时同化技术，实现地下水水情预警和预报，为地下水资源的优化管理和合理配置提供可靠定量的技术支持。对于地质环境敏感区，可将水流模型延伸应用，使用实时数据校准并同化地面沉降模型，在真正意义上实现关键地区地面沉降早期预警。

以上所述仅是本发明的优选实施方式，而非对其限制；应当指出，尽管参照上述各实施例对本发明进行了详细说明，本领域的普通技术人员应当理解，其依然可以对上述各实施例所记载的技术方案进行修改，或对其中部分或者全部技术特征进行等同替换；而这些修改和替换，并不使相应的技术方案的本质脱离本发明各实施例技术方案的范围。