一种欠定盲分离中的机械振源数估计方法与流程

本发明涉及机械设备多故障复合诊断技术，特别涉及一种欠定盲分离中的机械振源数估计方法。

背景技术：

多故障复合诊断是机械故障诊断中的一个难点，复合故障与其中单个故障虽然有所关系，但振动的各种表现是不一样的，复合故障并不是单个故障简单的叠加，故障之间是互相影响的，从而产生更丰富的振动形态。在工程实际中，若能把各种故障信号分离出来，则可以根据各种故障的振动特点很容易诊断。20世纪90年代兴起的盲源分离技术为机械的多故障并发的诊断提供了一种新的思路。盲源分离的基本含义是指未知源信号的概率分布和系统的传递函数的情况下，用一组传感器测得的混合信号中分离出独立源信号的一种技术。

然而，传统的多振源分离方法都不具备对未知信号源个数进行估计的能力，只能在假定械源数事先已知的情况下才能进行计算，否则无法进行盲源分离。然而，在实际中，械源信号的个数是未知的，甚至在机器运行过程中还可能是动态变化的，这就给机械故障分离带来了很大的困难，大大限制了盲源分离方法在机械振源分离中的应用。

目前，虽然人们能见到一些源信号数的估计方法，例如，文献[1,2]提出了一种基于奇异值分解的聚类分析NIS估计新方法，该方法可以给出一个机械系统中不相关源数的上界估计,从而合理配置信号检测传感器的数量，获得具有足够维数的观测信号，保证ICA方法在旋转机械源分离中的顺利实施。但是该方法的缺陷在于它只能估计出混合信号中不相关源数的上限，并不能给出其中振源的准确数目。文献[3]利用信息论准则如Aikaike信息准则(Aikaike Information Criterion，AIC)、最小描述长度(Minimum description Length，MDL)进行信源估计，该算法较为简便。文献[4]提出了基于独立分量分析与聚类分析的信源数估计算法，能够准确估计振源数；文献[5]提出了利用Gerschgorin圆盘定理判断信源个数，该算法能够用于有色噪声环境中；文献[6,7]提出了一种基于贝叶斯推论的机械源数估计方法。然而以上算法只适用于超定或额定混合条件下，即观测信号数大于或等于源信号数的情况。而对于观测信号数小于源信号数的情况下的源数估计问题并没有考虑。

近年来，平行因子(Parallel Factor，PARAFAC)因其在宽松约束条件下模型分解具有唯一性而备受关注，众多专家学者对PARAFAC模型分解唯一性进行了研究，现已广泛应用于环境与资源利用^[8]、化学计量^[9]、通信与信号处理^[10]等领域中。其中值得关注的是在化学计量领域中，学者们利用平行因子分析对未知干扰系统进行组分定量分析时，一般需要利用核一致诊断法先对系统组分数进行预估并得到最佳组分数，从而使得PARAFAC模型分解得到有物理意义的解。

技术实现要素：

基于上述背景技术，本发明提出一种基于平行因子分析和核一致诊断的欠定盲源数估计方法。利用二阶非平稳源分离(SONS)的基本思想和机械振动信号的非平稳性，首先将中心化传感器数据分成不重叠的数据块，然后计算各数据块的单一时延协方差矩阵并叠加成三阶张量，即平行因子模型；最后利用核一致诊断算法估计PARAFAC模型的最佳组分数，从而得到机械振源数的估计。由于该PARAFAC模型在欠定条件下依然满足唯一可辨识性，故能够解决欠定盲源分离下的机械振源数估计问题。仿真和实验结果验证了提出的方法的有效性。

为实现上述目的，本发明采取以下技术方案。欠定盲分离中机械振源数估计方法，其特征在于，其具体步骤为：

1)对N个观测信号x(t)进行中心化处理后，得到

2)将预处理后的观测数据分成L个非重叠的块，每块的时间窗T_l，并估计观测信号各段数据块的时滞协方差矩阵R_x∈C^N×N；

3)将L块数据段的时滞协方差矩阵组叠加成三阶张量R∈C^N×N×L；

4)采用平行因子模型的三线性交替最小二乘算法对3阶张量进行低秩分解；

5)通过核一致诊断算法，估计出最佳因子数M，即振动源数为M。

本发明的基本思想是利用二阶非平稳源分离(SONS)思想，将中心化传感器数据分成不重叠的数据块，计算各数据块的单一时延协方差矩阵并叠加成三阶张量，即平行因子(PARAFAC)模型；然后利用核一致诊断算法估计PARAFAC模型的最佳组分数，从而得到机械系统的振源数。

本发明充分利用了建立的平行因子模型在欠定条件下依然满足唯一可辨识性的特性，很好地解决了欠定盲源分离下的机械振源数估计问题。其有益效果主要体现在以下方面：

(1)在工程实际中，欠定盲源分离研究比超定和额定盲源分离的研究更有意义。传统的机械振源数估计方法仅适合超定或额定混合条件下。而提出的方法不仅适合超定或额定的盲源分离，而且还解决了欠定盲源分离下的机械振源数估计问题。

(2)建立的PARAFAC模型在欠定条件下依然满足唯一可辨识性，从而保证了该方法能够解决欠定盲源分离下的源数估计问题。

(3)提出的方法充分利用核一致诊断算法估计PARAFAC模型的最佳组分数，从而能够准确地估计出机械系统的振源数。

该方法在机械设备多故障复合诊断中具有广阔的应用前景。

附图说明

图1是平行因子模型结构示意图；

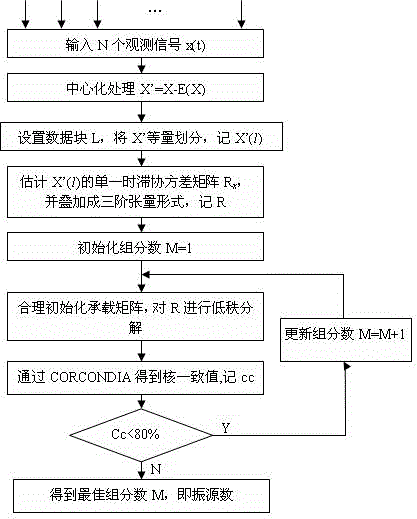
图2是本发明基于PARAFAC的欠定盲分离中机械振源数估计方法的流程图；

图3是本发明源信号时域波形图；

图4是本发明源信号频谱图；

图5是本发明观测信号时域波形图；

图6是本发明观测信号频谱图；

图7是本发明观测信号短时傅里叶变换时频特征图；

图8是本发明基于核一致诊断法的源个数估计图；

图9是本发明在不同数据块长度条件下的估计性能比较图；

图10是本发明在不同数据块数条件下的估计性能比较图；

图11是本发明实施例中电机—减速箱耦合实验装置结构示意图；

图12是本发明工程实验实例中的观测信号波形图；

图13是本发明工程实验实例中基于核一致诊断法的振动源数估计图。

图中：1-大电机，2-齿轮减速箱，3-负载设备，4-第一干扰电机，5-第二干扰电机，6-第一传感器，7-第二传感器。

具体实施方式

以下结合附图、实施原理、仿真和工程应用例子对本发明作进一步说明，参见图1至图13。

1.平行因子分析理论基础：

平行因子模型^[11]是一种多维矩阵低秩分解模型，又称为三线性模型，其模型如图1所示。三维矩阵X∈C^I×J×N的PARAFAC分解标量形式可表示为：

其中：i＝1,2,...,I，j＝1,2,...,J，n＝1,2,...,N，m＝1,2,...,M；A∈C^I×M、B∈C^J×M和C∈C^N×M分别为该模型的三个承载矩阵；E∈C^I×J×N为噪声矩阵。三线性模型亦可写成切片形式：

其中：D_i(A)为由矩阵A的第i行元素构成的对角矩阵。与二维矩阵低秩分解有所不同，PARAFAC模型分解在没有任何额外的约束条件下，具有唯一性。为了讨论PARAFAC模型是否具有可辨识性，引入矩阵k-秩的定义和PARAFAC模型唯一性定理。

矩阵k-秩定义^[12]：对于给定的矩阵A∈C^I×M，当且仅当A包含至少r个独立的列时，A的秩为

r_A＝Rank(A)＝r (3)

如果矩阵A的任意k列独立，则A的k-秩k_A＝k。

PARAFAC唯一性定理^[13]：若矩阵A、B和C的k-秩满足

k_A+k_B+k_c≥2(M+1) (4)

则由三维矩阵X分解得到承载矩阵A、B和C对于列交换和尺度变换是唯一的。若3个承载矩阵都满足k-秩条件，则可辨识的充分条件为

min(I,M)+min(J,M)+min(N,M)≥2M+2 (5)

2.欠定盲源数估计算法：

2.1构建PARAFAC模型：

考虑瞬时混合模型的盲源分离模型：

X(t)＝A(t)·S(t)+E(t) (6)

式中，S(t)＝[s₁(t),s(t),…,s_M(t)]^T为M个源信号构成的向量；X(t)＝[x₁(t),x₂(t),…,x_N(t)]^T为N个传感器所感测到的信号构成的向量；A(t)为N×M维混合矩阵；E(t)为附加的噪声信号。在实际应用中，受到传感器个数的限制，源信号的个数往往是多于混合信号的个数的，而且源信号的个数往往又是未知的，因此，这里仅考虑欠定的盲源分离情形，即N＜M。

假设每一个观测信号包含K个采样点，这里，利用二阶非平稳源分离(SONS)的主要思想^[14]，首先对各传感器数据进行中心化预处理，然后对各预处理后的信号分成不重叠的L(可整除)段数据块，每段数据块包含N_l＝K/L个数据点，用l＝1,...,L标志数据块。由此，式(6)亦可表示为：

X(l,t)＝A(t)·S(l,t)+E(l,t) (7)

式中：X(l,t)＝[x₁(l,t),...,x_N(l,t)]^T；S(l,t)＝[s₁(l,t),...s_M(l,t)]^T；并估计观测信号各段数据块的时滞协方差矩阵R_x，有

式中，A∈R_n×m是混合矩阵，τ_i是时间延迟，i＝1,2,...,I。序号T_l表示第l个时间窗口。在此针对单一时延τ₁＝0协方差矩阵(即I＝1)，有

其中，源时滞协方差矩阵为

假设源信号S(t)＝[s₁(t),s(t),…,s_M(t)]^T之间互不相关，则源时滞协方差矩阵R_s为对角矩阵。

将各段数据块时滞协方差R_x(T_l,τ₁)叠加成三阶张量记为R_n1,n2,l，其中n₁＝1,...,N，n₂＝1,...,N，l＝1,...,L；A中的元素记为a_n×m；构建一个矩阵M×L维矩阵C，其表达式为

根据式(9)可改写为

记其标量形式为：

其中n1＝1,2,...,N；n2＝1,2,...,N；与式(1)对比可知，式(13)为PARAFAC分解模型。

2.2模型可辨识性：

由定理1可知，式(13)唯一性分解的条件为

式中：k_A＝min(N,M)，代入式(14)可得

式(15)为唯一性分解的充分条件，适用于实数域和复数域。根据机械振动信号的非平稳性，C^*必然是列满秩，即

设M≤L，3阶张量唯一性分解条件为

2M(M-1)≤N²(N-1)² (17)

2.3核一致诊断法：

在PARAFAC分解模型具有可辨识性条件下，PARAFAC模型中因子数也具有唯一性。为了对模型的组分数进行确定，通常采用由Bro等提出的核一致诊断算法(The core consistency diagnostic)来测定^[15]。利用核一致诊断法对上述构建的PARAFAC模型进行求解，得到的最佳组分数与机械振动系统的振源数相对应。核一致诊断法通过计算PARAFAC模型中的超对角阵T和truck3模型中的立方阵G之间的相似程度，即核一致来估计组分数

M是模型的组分数；g_abc为立方阵G的元素；t_abc是超对角阵T的元素。对于可辨识的的PARAFAC模型，立方阵T和truck3模型的立方阵G非常相似，此时的核一致值会等于100％。一般来说，只要核一致值大于或等于80％，则可认为符合三线性模型，但当核一致值低于40％时，可认为偏离三线性模型。因此可以根据核一致值的变化来确定最佳组分数，即振动源个数。

2.4算法具体步骤：

综合以上分析，给出提出的方法的框图，如图2所示，具体步骤如下：

(1)对各路观测信号进行中心化处理后，得到

(2)将预处理后的观测数据分成L个非重叠的块(时间窗T_l)，并估计观测信号各段数据块的时滞协方差矩阵R_x∈C^N×N。

(3)将L块数据段的时滞协方差矩阵组叠加成三阶张量R∈C^N×N×L。

(4)采用PARAFAC模型的三线性交替最小二乘(TALS)算法对3阶张量进行低秩分解。

(5)通过核一致诊断算法，估计出最佳因子数M，即振动源数为M。

3.仿真研究：

针对机械系统振动信号，在仿真实验中，我们模拟以下4个原始信号源：源信号1为调制信号，模拟齿轮振动源信号，其载波频率为f_c＝40Hz，调制频率为f_Ω＝30Hz。源信号2与1相似模拟齿轮振动源信号，载波频率相同，但调制频率为f_Ω＝20Hz，用于模拟同轴上不同齿轮的啮合振动。源信号3为周期振动冲击信号，用于模拟机械系统中常见的冲击振动。源信号4为谐波信号，基波频率为f₀＝10Hz用于模拟轴和轴系在旋转运动中产生的振动是由不平衡、不对中等原因引起的振动。源信号生成函数如下：

仿真源信号时域波形及频谱图如图3、图4所示。采样频率f_s＝1000Hz，采样点数N＝10240。设置混合矩阵取值范围在[0～1]区间。假设传感器尽可能靠近源信号的话，这是一个实际的近似信号。可以认为随着传感器与故障源距离的增加，检测故障的能力降低，这样，传感器尽量靠近故障监测点对于故障诊断是十分重要的。当i＝j时，参数A_ij＝1，即混合矩阵为：

为了得到观测矩阵，将混合矩阵A与源信号S(t)相乘得到的观测信号时域波形及频谱图如图5、图6所示。由图5可以看出，源信号数为4，观测信号数为3，是一个欠定盲源分离问题。观测信号波形复杂，无法从观测信号中直接评估独立组成成分波形以及数目。而图6的观测信号中均存在源信号的特征频率，四路信号完全相互干扰混在一起。对传感器观测信号进行短时傅里叶变换，得到其时频特征信息如图7所示，由图7可以看出，短时傅里叶变换对解决多信号混叠情况存在明显的不足，很难从不同的混叠信号中得到振源数。

由于观测信号成分复杂，无法预知机械系统中的振源数，故需采用核一致诊断法来估计系统中的振源数。这里，通过PARAFAC和二阶非平稳源分离联合构造PARAFAC模型，并利用核一致诊断对PARAFAC模型求解得到模型因子数，即振动源数。首先对各观测信号的10240个采样点进行去均值化预处理，然后将其分割成10块不重叠的数据段，每个数据段包含1024个数据点，并在此基础上，得到每一块数据块相应的3×3维时滞协方差矩阵，接着将10块数据段各自的时滞协方差矩阵叠加成3阶张量形式，采用PARAFAC模型的三线性交替最小二乘算法(TALS)对模型进行低秩分解，得到载荷矩阵。通过核一致诊断算法，估计出最佳组分数，从而得到振动源数。图8为所研究模型不同组分数对核一致值得影响。显然，当组分数小于等于4时，对应的核一致值均大于80％；当组分数大于4时，对应核一致值趋近于0，由此可以估计出最佳因子数等于4，即振动源数M＝4。

为了验证提出的方法的性能，采用Monte Carlo仿真来评估算法的振源估计性能。图9是在不同的数据块长度下该算法的信源个数估计性能比较，延用前面仿真信号，振源数目为4，传感器数目为3，数据块数为20，设定信噪比范围为0—10dB，设置每块数据段分别为1024、2048、3072时，其他仿真条件不变。从图9中可以看出，该算法的信源估计性能随着N的增加而变好。图10是在不同的数据块数下该算法的信源个数估计性能比较，振源数目为4，传感器数目为3，每段数据块为2048，设定信噪比范围为0—10dB，设置数据块数分别为10、20、30，其他仿真条件不变。从图10中可以看出，该算法的信源估计性能随着L的增加而变好。

4.工程实验实例：

本实验采用如图11所示的电机—减速箱耦合实验装置，用于验证所提算法在机械多振源系统中源数估计的有效性。设置三个振源装置：主机组包括大电机1和齿轮减速箱2，且大电机1与齿轮减速箱2连接，齿轮减速箱2连接有负载设备3，大电机1的一侧设置有第一干扰电机4，负载设备3的一侧安装有第二干扰电机5。在上述实验装置内，本着传感器尽量靠近振源点的原则，将第一传感器6安装于大电机1(2.2kw)壳体上，将第二传感器7安装于第二干扰电机5上。当各设备同时运行时，由第一传感器6和第二传感器7可共同获得二通道的混合振动观测信号x。在具体实验中，采用定频率等间隔采样策略，采样频率为5kHz(为清楚起见，仅给出前4096样本点)。观测信号波形分别如图12所示，从图12中可看出观测混合信号波形复杂，难以有效评估出蕴涵其中的振源波形和数目信息。实验台设置的振源数目为3(源于三台电动机运行振动)。

利用PARAFAC的核一致诊断法估计了二通道壳体结构实验台观测混合信号的振源数目，分析结果如图13所示。当M≤3时，核一致值接近100；当M>3时，核一致值趋近于0，由此可以估计出最佳因子数M＝3，即振动源个数为3。

参考文献：

1.焦卫东,杨世锡,吴昭同.基于源数估计的旋转机械盲源分离[J].中国机械工程,2003,14(14):1184-1187.

2.焦卫东.基于独立分量分析的旋转机械故障诊断方法研究[D].浙江大学,2003.

3.Huang L,Long T,Wu S.Source enumeration for high-resolution array processing using improved Gerschgorin radii without eigendecomposition[J].IEEE Transactions on Signal Processing,2008,56(12):5916-5925.

4.成玮,何正嘉,张周锁.基于独立分量分析的壳体结构振源数目估计方法[J].机械工程学报,2014,(19):73-79.

5.Wu H-T,Yang J-F,Chen F-K.Source number estimators using transformed Gerschgorin radii[J].IEEE Transactions on Signal Processing,1995,43(6):1325-1333.

6.范涛,李志农,肖尧先.基于源数估计的机械源信号盲分离方法研究[J].机械强度,2011,33(1):15-19.

7.范涛.基于变分贝叶斯独立分量分析的机械故障诊断方法研究[D].郑州大学，2009.

8.Favier G.An overview of system modeling and identification(Invited paper)[C].11th International conference on Sciences and Techniques of Automatic control&computer engineering(STA'2010),Monastir,Tunisia,December 19-21,2010.

9.Mounier S,Raynaud M,Oursel B,et al.Fluorescence indexes and PARAFAC components-what is the best way？[C],2015:15639.

10.Zhang X,Cao R,Zhou M.Noncircular-PARAFAC for 2D-DOA estimation of noncircular signals in arbitrarily spaced acoustic vector-sensor array subjected to unknown locations[J].EURASIP Journal on Advances in Signal Processing,2013,2013(1):1-10.

11.Harshman RA.Foundations of the PARAFAC procedure:Models and conditions for an"explanatory"multi-modal factor analysis[J].1970.

12.Sidiropoulos ND,Bro R,Giannakis GB.Parallel factor analysis in sensor array processing[J].IEEE transactions on Signal Processing,2000,48(8):2377-2388.

13.Sidiropoulos ND,Giannakis GB,Bro R.Blind PARAFAC receivers for DS-CDMA systems[J].IEEE Transactions on Signal Processing,2000,48(3):810-823.

14.Choi S,Cichocki A,Belouchrani A.Blind separation of second-order nonstationary and temporally colored sources[C]:IEEE,2001:444-447.

15.Bro R,Kiers HA.A new efficient method for determining the number of components in PARAFAC models[J].Journal of chemometrics,2003,17(5):274-286.