一种航天器正弦扫频振动疲劳失效分析方法与流程

本发明涉及一种航天器正弦扫频振动疲劳失效分析方法，特别是航天器结构失效，属于飞行器设计技术领域。

背景技术：

马兴瑞、韩增尧等著《卫星与运载火箭力学环境分析方法及试验技术》中提到，航天器正弦振动环境属于低频瞬态环境，频率范围一般介于0～100Hz，主要由火箭发动机推力脉动、点火、关机、级间分离等事件引起。另外，在地面运输、装卸以及返回航天器在返回制动、开启降落伞、着陆等事件也产生低频瞬态环境。通常针对发射过程中，航天器经受最严酷的几个特征状态下(起飞，最大动压，助推级分离前，助推级分离后，一、二级分离前，一、二级分离后)，需要联合运载火箭和卫星进行动态星箭载荷耦合分析，也称星箭耦合分析。航天器正弦扫频振动试验时间历程比较短暂，而且航天器经历的发射段的振动试验历程较短，因此通常不分析其疲劳寿命。

GJB1027A-2005《运载器、上面级和航天器试验要求》和HDBK-7005《Dynamic environmental criteria》中提到，目前的分析方法是根据线性振动原理，利用有限元分析频域内加速度响应，根据以往振动试验经验判断是否失效，结合正弦扫频振动前后特征级扫频结果对比，频率漂移不超过5％为合格。但这种分析方法缺乏定量分析，没有损伤概念，并且在试验之前无法给出预示的损伤分析，更多依赖于经验数据。

根据刘旭华的《结构动力可靠性研究》和倪侃、张圣坤的《疲劳可靠性二维统计Miner准则》，现有的振动失效分为两种方法，首次穿越失效和疲劳失效，上述两种失效方法都是基于时域的振动响应幅值和循环次数来进行分析。

技术实现要素：

本发明解决的技术问题是：克服现有技术的不足，提供了一种航天器正弦扫频振动疲劳失效分析方法，解决航天器结构正弦扫频振动疲劳损伤分析问题，可以用于分析航天器正弦扫频振动的疲劳损伤和失效。

本发明的技术解决方案是：一种航天器正弦扫频振动疲劳失效分析方法，包括如下步骤：

(1)根据航天器结构，建立航天器的有限元模型，根据正弦扫频振动试验中航天器与夹具的连接方式，对其相连接的部分进行固定约束，并施加正弦扫频振动条件作为载荷，进行振动频域响应分析，得到加速度和应力频域响应结果；

(2)根据正弦扫频振动控制方法，将应力频域响应转化为应力时域响应幅值以及循环次数；

(3)根据应力时域响应幅值和循环次数，结合首次穿越失效以及疲劳损伤分析方法Miner准则，进行振动失效分析。

所述的将应力频域响应转化为应力时域响应幅值以及循环次数的方法包括如下步骤：

(1)根据应力频域响应结果得到应力时域响应幅值；

(2)计算得到频率处循环次数n为

其中，f₁、f₂为扫描倍频程过程中任意两个频率点，t₁为扫描至f₁时间，t₂为扫描至f₂时间，s为倍频程扫描速率，f₀为扫描开始频率。

所述的s为4.33oct/min。

本发明与现有技术相比的优点在于：

(1)本发明方法克服了现有的分析方法在试验之前无法给出预示的损伤分析，更多依赖于经验数据的缺陷，通过将频域分析结果转化为时域分析结果，从而和现有的失效理论结合起来，可以用于振动失效分析。更加直观，可以直接用于振动失效分析，具有很好的使用价值；

(2)本发明方法克服了现有的分析方法缺乏定量分析，没有损伤概念，无法定量分析振动试验造成的损伤的缺陷，可以给出定量的疲劳损伤分析结果，用于评价正弦振动试验的影响。

附图说明

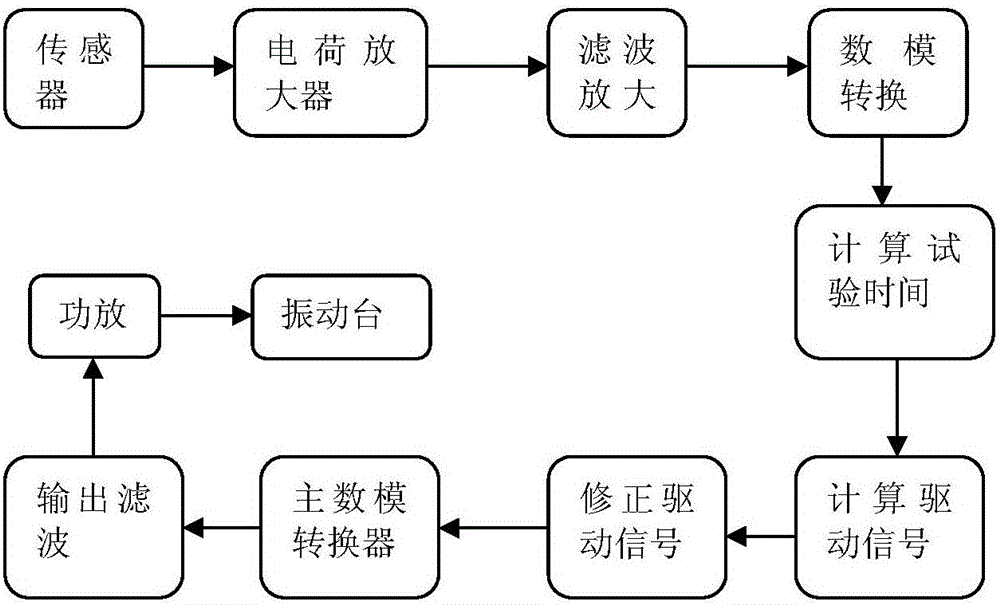
图1为本发明一种航天器正弦扫频振动疲劳失效分析方法流程图；

图2为本发明方法中正弦振动控制框图。

具体实施方式

本发明针对现有技术的不足，提出一种航天器正弦扫频振动疲劳失效分析方法，解决航天器结构正弦扫频振动疲劳损伤分析问题，可以用于分析航天器正弦扫频振动的疲劳损伤和失效，下面结合附图对本发明方法进行详细说明。

如图1所示为本发明一种航天器正弦扫频振动疲劳失效分析方法流程图，包括如下步骤：

(1)根据航天器结构，建立航天器的有限元模型，根据正弦扫频振动试验中航天器与夹具的连接方式，对其相连接的部分进行固定约束，并施加正弦扫频振动条件作为载荷，进行振动频域响应分析，得到加速度和应力频域响应结果；

(2)根据正弦扫频振动控制框方法，将应力频域响应转化为应力时域响应幅值以及循环次数；

(3)根据应力时域响应幅值和循环次数，结合首次穿越失效以及疲劳损伤分析方法Miner准则，进行振动失效分析。

如图2所示为本发明方法中正弦振动控制框图，扫描倍频程时，扫描时间和扫描速率的关系用下式表示：

式中：f₀为扫描开始频率；f_x为扫描终止频率；s为倍频程扫描速率，单位Oct/min；t为从f₀扫到f_x所需时间，单位为min。

对于正弦振动，关注结构谐振响应，进行失效分析结构的自然频率是f_n，谐振响应曲线是一条有谐振峰的曲线，峰值与Q(结构放大系数)有关，谐振峰的频率范围与结构阻尼有关，试验表明在谐振状态下结构失效主要取决于谐振带宽Δf内的振动循环次数，为此公式(1)可以写为：

式中：Δf为谐振带宽，Δt为谐振带宽的持续时间。

根据振动理论上式可写为

假设放大系数Q＝10，经过结构谐振带宽的时间△t应与外场环境基本一致，大约为2秒(1/30分钟)，所以扫描频率的计算结果是S≈4.33oct/min。

由公式(1)可得：

式中：f₁、f₂为扫描过程中任意两个频率点，t₁为扫描至f₁时间，t₂为扫描至f₂时间。以来代替f₁至f₂的频段，则在频率处循环的次数n为：

在5～100Hz内取96个频率点，在MATLAB中编程计算，采用鉴定试验的扫描速率2Oct/min，则在所取的96个频率点上，所循环的次数都为42.8302次，约为43次。以验收试验的扫描速率4Oct/min来计算，则在96个频率点上，所循环的次数都为21.64次，约为22次。

根据步骤(1)得到的应力幅值和前文计算的循环次数，可以进行首次穿越失效分析和疲劳失效分析。

本发明说明书中未作详细描述的内容属本领域技术人员的公知技术。