砂泥岩储层地层压力的地震预测方法及装置与流程
本发明涉及石油与天然气勘探中地层压力预测技术领域,特别涉及一种砂泥岩储层地层压力的地震预测方法及装置。
背景技术:
地层压力的研究至今已有40多年的历史,期间众多学者都针对当时的最新研究成果对地层压力提出了各种预测方法,主要包括测井方法和地震方法。不论是利用测井方法还是结合地震方法,大部分都是利用有效压力与速度之间的关系来预测孔隙压力,其中最重要的理论基础就是Terzaghi在1943年提出的有效压力原理,现在大多数速度与孔隙压力转换公式都是基于这一原理提出的。Hottman和Johnsom在1965年利用声波速度曲线,提出等效深度法来预测孔隙压力。Pennebaker于1968年提出利用由叠加速度获得的地震层速度来预测孔隙压力的方法。Bilgeri和Ademeno在1982年利用二维地震速度数据很好地预测了地层孔隙压力。Lee等人在1998年利用层析反演速度对南里海的孔隙压力进行了很好的预测。Swan在2001年利用AVO梯度的低频正交分量来识别叠加速度的误差,进而提出了一种新的通过AVO技术求取速度进而计算孔隙压力的方案。Khazanehdari和Dutta于2006年在Swan提出方案的基础上又提出了一种整合测井、地质和地震数据的综合孔隙压力预测(iPPP)方法。
在生产中广泛应用的有Eaton于1975年提出的通过地震速度来估算有效压力垂直分量的经验公式,Bowers在1995年提出的适用于欠压实和流体膨胀机制产生的异常压力的速度和有效压力关系式。Fillippone提出孔隙压力经验公式,克服了依赖正常压实趋势的缺点。Eberhart-Phillips等人在1989年提出一个经验公式,将纵波速度、泥质含量和孔隙度与有效应力联系起来。Yan和Han于2009年在Han的数据基础上提出速度关于有效压力的关系式,并在此公式的基础上Yan和Han在2012年对Eaton公式进行了进一步的改进。
综上,现有技术砂泥岩储层地层压力地震预测方法主要存在的问题是:1、传统方法仅仅是利用地震速度这一单一参数来反应地层压力变化;2、传统方法对于地层异常压力的理论机制太单一。因此,在对砂泥岩储层地层压力的预测时,预测精确度低。
技术实现要素:
本发明实施例提供了一种砂泥岩储层地层压力的地震预测方法,用以提高地层压力预测的精确度,该方法包括:
基于Hashin-Shtrikman边界模型,根据研究区域内目标砂泥岩储层的孔隙度和泥质含量,计算目标砂泥岩储层在极限有效应力下的弹性模量,微裂隙密度因素和微裂隙闭合率因素;根据极限有效应力下的弹性模量,微裂隙密度因素和微裂隙闭合率因素,确定干燥岩石弹性模量与有效应力的关系;
根据干燥岩石弹性模量与有效应力的关系,以及研究区域内的测井数据,确定砂泥岩随深度变化的有效应力系数;
根据干燥岩石弹性模量与有效应力的关系,以及砂泥岩随深度变化的有效应力系数,对研究区域内单口井的所有待测目标层位进行地层压力预测;根据干燥岩石弹性模量与有效应力的关系,以及有效应力系数,利用反演得到的弹性模量数据体,以单口井的地层压力为约束,对研究区域进行三维地震地层压力预测。
本发明实施例还提供了一种砂泥岩储层地层压力的地震预测装置,用以提高地层压力预测的精确度,该装置包括:
弹性模量与有效应力关系确定模块,用于基于Hashin-Shtrikman边界模型,根据研究区域内目标砂泥岩储层的孔隙度和泥质含量,计算目标砂泥岩储层在极限有效应力下的弹性模量,微裂隙密度因素和微裂隙闭合率因素;根据极限有效应力下的弹性模量,微裂隙密度因素和微裂隙闭合率因素,确定干燥岩石弹性模量与有效应力的关系;
有效应力系数确定模块,用于根据干燥岩石弹性模量与有效应力的关系,以及研究区域内的测井数据,确定砂泥岩随深度变化的有效应力系数;
地层压力预测模块,用于根据干燥岩石弹性模量与有效应力的关系,以及砂泥岩随深度变化的有效应力系数,对研究区域内单口井的所有待测目标层位进行地层压力预测;根据干燥岩石弹性模量与有效应力的关系,以及有效应力系数,利用反演得到的弹性模量数据体,以单口井的地层压力为约束,对研究区域进行三维地震地层压力预测。
与现有技术相比,本发明实施例提供的技术方案,具备的有益效果在于:
首先,与现有技术相比,本发明实施例提供的技术方案,不仅仅是利用地震速度这一单一参数来反应地层压力变化,而是考虑了研究区域内目标砂泥岩储层的孔隙度和泥质含量等因素,较传统方法而言,能更加准确地预测出地层压力;
其次,传统方法仅仅依据对于地层异常压力的单一理论机制,与现有技术相比,本发明实施例通过:基于Hashin-Shtrikman边界模型,根据研究区域内目标砂泥岩储层的孔隙度和泥质含量,计算目标砂泥岩储层在极限有效应力下的弹性模量,微裂隙密度因素和微裂隙闭合率因素;根据极限有效应力下的弹性模量,微裂隙密度因素和微裂隙闭合率因素,确定干燥岩石弹性模量与有效应力的关系的技术方案,可以计算得到准确的有效应力,进而获得准确的地层压力。
综上所述,本发明实施例提供的技术方案提高了地层压力预测的精确度。
附图说明
此处所说明的附图用来提供对本发明的进一步理解,构成本申请的一部分,并不构成对本发明的限定。在附图中:
图1是本发明实施例中砂泥岩储层地层压力的地震预测方法的流程示意图;
图2a是本发明实施例中干燥岩石纵波速度与有效应力关系曲线示意图;
图2b是本发明实施例中干燥岩石横波速度与有效应力关系曲线示意图;
图3a是本发明实施例中样品S3的弹性模量与有效应力曲线关系;
图3b是本发明实施例中样品相对弹性模量与有效应力变化曲线示意图;
图4a和图4b是本发明实施例中弹性模量、有效应力、极限弹性模量Mlim关系曲线示意图,其中,图4a为系数A=0.1时,系数B对有效应力预测模型(弹性模量与有效应力的关系)的影响,图4b为A=1时,系数B对有效应力预测模型(弹性模量与有效应力的关系)的影响;
图5是本发明实施例中有效应力预测模型(干燥岩石弹性模量与有效应力的关系)计算成果示意图;
图6是本发明实施例中研究区域内选出的单口井LN1的砂泥岩参数值示意图;
图7是本发明实施例中LN1井地层压力示意图;
图8是本发明实施例中泥质含量回归分析示意图;
图9是本发明实施例中孔隙度计算结果交会图示意图;
图10是本发明实施例中泥质含量地震资料反演结果示意图;
图11是本发明实施例中孔隙度地震资料反演结果示意图;
图12是本发明实施例中Eaton方法计算的地层压力示意图;
图13是本发明实施例中本文研究方法计算的地层压力示意图;
图14是本发明实施例中砂泥岩储层地层压力的地震预测装置的结构示意图。
具体实施方式
为使本发明的目的、技术方案和优点更加清楚明白,下面结合实施方式和附图,对本发明做进一步详细说明。在此,本发明的示意性实施方式及其说明用于解释本发明,但并不作为对本发明的限定。
传统的地震地层压力预测方法主要有异常压力形成机制单一、参数使用单一和精度太低三个主要的缺陷,发明人考虑到上述问题,提出了一种砂泥岩储层地层压力地震预测新方法,下面对该方法进行详细介绍。
图1是本发明实施例中砂泥岩储层地层压力的地震预测方法的流程示意图,如图1所示,该方法包括如下步骤:
步骤101:基于Hashin-Shtrikman边界模型,根据研究区域内目标砂泥岩储层的孔隙度和泥质含量,计算目标砂泥岩储层在极限有效应力下的弹性模量,微裂隙密度因素和微裂隙闭合率因素;根据极限有效应力下的弹性模量,微裂隙密度因素和微裂隙闭合率因素,确定干燥岩石弹性模量与有效应力的关系;
步骤102:根据干燥岩石弹性模量与有效应力的关系,以及研究区域内的测井数据,确定砂泥岩随深度变化的有效应力系数;
步骤103:根据干燥岩石弹性模量与有效应力的关系,以及砂泥岩随深度变化的有效应力系数,对研究区域内单口井的所有待测目标层位进行地层压力预测;根据干燥岩石弹性模量与有效应力的关系,以及有效应力系数,利用反演得到的弹性模量数据体,以单口井的地层压力为约束,对研究区域进行三维地震地层压力预测。
与现有技术相比,本发明实施例提供的技术方案,具备的有益效果在于:
首先,与现有技术相比,本发明实施例提供的技术方案,不仅仅是利用地震速度这一单一参数来反应地层压力变化,而是考虑了研究区域内目标砂泥岩储层的孔隙度和泥质含量等因素,较传统方法而言,能更加准确地预测出地层压力;
其次,传统方法仅仅依据对于地层异常压力的单一理论机制,与现有技术相比,本发明实施例通过:基于Hashin-Shtrikman边界模型,根据研究区域内目标砂泥岩储层的孔隙度和泥质含量,计算目标砂泥岩储层在极限有效应力下的弹性模量,微裂隙密度因素和微裂隙闭合率因素;根据极限有效应力下的弹性模量,微裂隙密度因素和微裂隙闭合率因素,确定干燥岩石弹性模量与有效应力的关系的技术方案,可以计算得到准确的有效应力,进而获得准确的地层压力。
综上所述,本发明实施例提供的技术方案提高了地层压力预测的精确度。
本发明实施例中采取的技术路线是对储层岩样进行常规岩心分析,确定出孔隙度和泥质含量是影响有效应力的敏感性参数。通过改变储层岩样的围压,得到随围压变化的有效应力曲线,即弹性模量—有效应力,此曲线反映了岩石对压力的响应,其由三个参数:Mlim(极限有效应力下的弹性模量)、A(微裂隙密度因素)、B(微裂隙闭合率因素)控制。本发明的关键在于能够根据微裂缝密度、闭合率,孔隙度,泥质含量,矿物成分、孔隙流体性质等因素准确的确定出上述三个控制参数。在分析了储层的岩石物理参数后,就能够得到适合该地区的弹性模量—有效应力曲线关系,利用测井得到的有关密度、声波时差曲线得到弹性模量,带入到上述式子中得到较为准确的有效应力。其次,将砂泥岩分开来考虑,确定了考虑孔隙度和泥质含量的砂、泥岩有效应力系数,分别处理后再将数据整合在一起。有了有效应力,有效应力系数,再通过有效应力原理,求出地层压力。此方法应用到一口井上,就能进行单井地层压力预测。若利用地震反演得到的纵横波速度体、密度体,同时利用测井数据进行标定,就能进行三维地震地层压力预测。下面对上述步骤进行详细介绍。
在一个实施例中,上述步骤101中,在基于Hashin-Shtrikman边界模型,根据研究区域内目标砂泥岩储层的孔隙度和泥质含量,计算目标砂泥岩储层在极限有效应力下的弹性模量,微裂隙密度因素和微裂隙闭合率因素,之前还可以包括:
根据对目标砂泥岩储层的样品岩心分析,确定影响砂泥岩有效应力的关键参数;关键参数为:孔隙度和泥质含量。
具体实施时,在上述步骤101之前,还包括对影响砂泥岩储层有效应力的敏感性参数分析的步骤,下面对该步骤进行详细介绍如下。
砂泥岩物性参数的变化是储层敏感性的外在表现形式,而全矿物分析是从砂泥岩岩石内部组成上对储层敏感性进行预测。常规的储层敏感性分析研究是建立在岩心分析基础之上,本发明在进行应力敏感性实验前,对所做的岩心进行了X射线衍射全矿物含量分析,以便从微观上了解岩样的矿物组成和孔隙结构。
本部分岩心全矿物分析实验结果如表1所示。
表1
因此,发明人将在实际储层开发区钻取适合室内实验的圆柱状岩样,并对岩样的孔隙度、渗透率、孔隙结构、润湿性、泥质含量等进行常规岩心分析,对实验数据进行分析后,最终确定出影响储层有效应力的敏感性参数为孔隙度和泥质含量。并且从测井曲线中估算岩石物理参数,比如孔隙度、泥质含量、含水饱和度、围压、弹性模量等。
在一个实施例中,上述步骤101中,基于Hashin-Shtrikman边界模型,根据研究区域内目标砂泥岩储层的孔隙度和泥质含量,计算目标砂泥岩储层在极限有效应力下的弹性模量,微裂隙密度因素和微裂隙闭合率因素,可以包括:
基于Hashin-Shtrikman边界模型,根据研究区域内目标砂泥岩储层的孔隙度和泥质含量,计算目标砂泥岩储层在极限有效应力下的弹性模量;
根据目标砂泥岩储层的围压和目标储层的实测地层压力,计算目标砂泥岩储层的有效应力;
根据目标砂泥岩储层在极限有效应力下的弹性模量,有效应力,以及测井密度和声波时差数据,得到微裂隙密度因素和微裂隙闭合率因素。
具体实施时,基于Hashin-Shtrikman边界模型,Gassmann流体替换原理,多矿物最优化测井解释原理,利用上述预测得到的孔隙度、泥质含量、孔隙流体,计算出在极限有效应力下的弹性模量Mlim;利用计算出的Mlim,有效应力(有效应力可由围压、实测地层压力,并且令有效应力系数n为1,使用上覆地层压力和RFT数据求出),以及测井密度和声波时差曲线,通过最小二乘反演方法拟合出微裂隙密度因素A和微裂隙闭合率因素B这两个控制参数,进而后续确定砂泥岩储层的弹性模量与有效应力的理论关系。
在一个实施例中,所述干燥岩石弹性模量与有效应力的关系可以为:
M=Mlim(1-A exp(-Pd/B));
其中,M为干燥岩石弹性模量,Pd为干燥样品压力变化和饱水岩石有效应力,Mlim为极限有效应力下的弹性模量,A为砂泥岩储层的微裂隙密度因素,B为砂泥岩储层的微裂隙闭合率因素。
下面举一例说明干燥岩石弹性模量与有效应力的关系是如何得到的。
为了获取干燥岩石弹性模量与压力的关系,本项研究对岩心在不同压力条件下的声学参数进行了实验分析工作。
本项研究对岩心的弹性模量的测量,主要是在于对其速度的测量,采用的是脉冲方法。实验测试基本原理如下:是从岩心的一个方向给一个脉冲,然后从另一个相对的方向进行测量,测量这个脉冲的到达时间,最后根据测量距离和时间,计算出岩心的速度。研究速度与有效应力关系的方法如下:保持孔隙压力不变,通过多次加载和卸载围压,获得稳定的干燥岩石速度与有效应力的关系,进而获得干燥岩石的弹性模量-有效应力关系曲线。
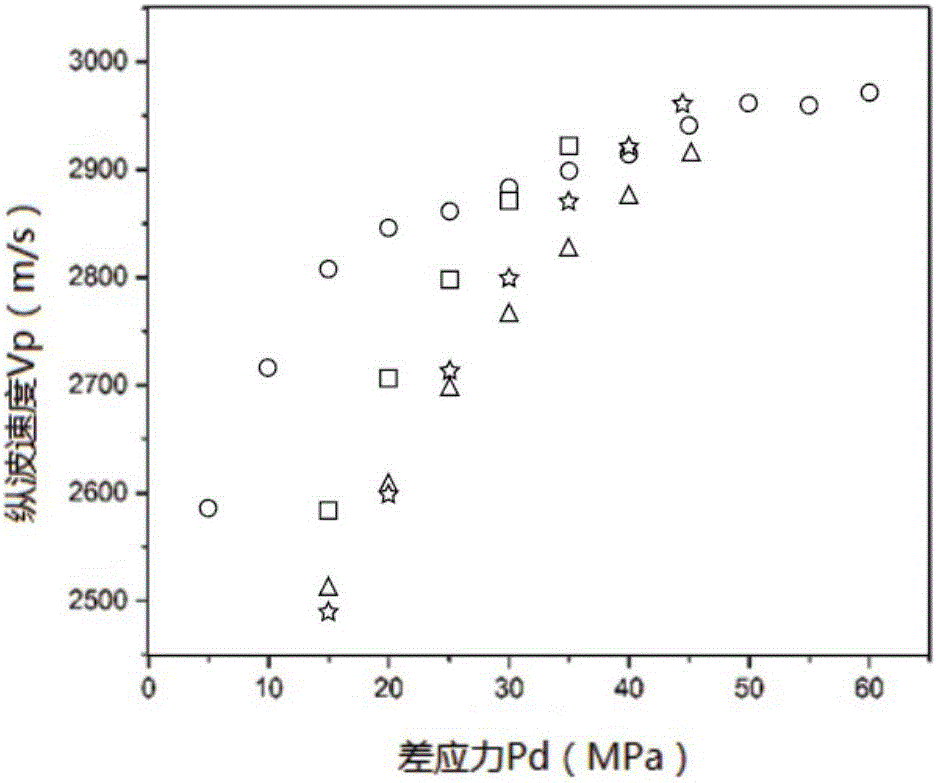
取自准格尔盆地的曲流点砂坝的S1、S2、S3、S4这4个样品,所有样品都是固结完好的泥质砂岩,这些岩心样品主要是中等孔隙度(8%-16%),对S1、S2、S4样品施加5MPa-40MPa围压,对S3样品施加5MPa-60MPa围压,分别测得响应的纵横波速度。测试结果如图2a和2b所示,纵横波随有效压力增加呈现类似的非线性增加,纵横波速在5MPa-40MPa围压下的快速增加可能是由于低纵横比孔隙的闭合引起的。图2a和图2b中四种不同的形状分别代表了S1、S2、S3、S4这4个样品。我们利用不同围压下的速度和密度测量数据就能计算出样品的纵波模量和剪切模量。图3a显示了S3样品的弹性模量—有效应力曲线。可以看出弹性模量—有效应力关系是非线性的,在有效压力增加初期,弹性模量会快速增加,当有效压力增加到一定程度时,弹性模量增加速度减慢。并且纵波模量的增加幅度比剪切模量的增加幅度要显著。在有效压力增加初期,纵波模量快速增加要归因于类似微裂缝、岩石骨架中的弱颗粒接触等低纵横比孔隙的闭合。
另外,本发明附图中的差应力与有效应力为同一概念。
Dvorkin et al(1996)使用公开测试数据,对干燥砂岩的弹性模量随有效压力变化进行研究,并且发现相对弹性模量-孔隙度的散点图显示出高孔隙度下的低分散性,低孔隙度的高分散性,根据Dvorkin的概念,我们由计算出的弹性模量算出了相对体积模量变化。图3b显示了相对体积模量变化随有效压力的变化,呈指数变化的曲线很好的拟合了这些数据点,于是我们利用这些样品得出了弹性模量—有效应力的公式,其公式如下所示:
经过综合整理,我们得到了:
M=Mlim(1-Aexp(-Pd/B));(2)
其中,M为干燥岩石弹性模量,Pd为砂泥岩储层有效应力,Mlim为极限有效应力下的弹性模量,A为砂泥岩储层的微裂隙密度因素,B为砂泥岩储层的微裂隙闭合率因素。
具体实施时,所述Hashin-Shtrikman边界模型为:
Mlim基于Hashin-Shtrikman边界模型原理,取自弹性模量的上边界,其数值为极限有效应力下的弹性模量。
其中,KHS+为砂泥岩骨架体积模量Hashin-Shtrikman上界限,μHS+为砂泥岩骨架剪切模量Hashin-Shtrikman上界限,Kmax为砂泥岩矿物最大体积模量,μmax为砂泥岩矿物最大剪切模量,r1为砂岩的成分含量,r2为泥岩的成分含量,r3为孔隙成分含量,C(h)是深度h处的泥质含量,Φ(h)是深度h处的孔隙度。
在本文中,将Mlim等效为KHS+,其计算公式如(3)-(5)所示。
如图4a和图4b所示,定义系数A为微裂隙密度因素,其与微裂隙的密度和体积有关,并随着有效压力的变化而变化,系数B为微裂隙闭合率因素,其与孔隙结构和低纵横比孔隙密切相关,是控制弹性模量与有效应力曲线形状的关键因素。可从图4a和图4b中看出系数A越大,弹性模量的变化越大,系数B越低,孔隙闭合的压力越小。值得注意的是当系数A=0时(所有的疏松孔隙闭合),该模型曲线近似为一条直线当系数A=1时,模型曲线与Carcione et al(2003)推导出的曲线一致。
本发明实施例中的砂泥岩弹性模量与有效应力的关系可以为如图4a和图4b所示的关系曲线图,也可以是表格或是建立的预测模型等等。
以图5的实例作为参考,我们可以根据储层微裂缝密度、闭合率,孔隙度,泥质含量,矿物成分、孔隙流体性质等因素准确的确定出三个控制参数Mlim、A、B,进而确定出能反映储层岩性的有效应力模型,图5第一列给出了孔隙度和泥质含量,第二列描述了储层的岩性,第三列给出了声波时差和密度曲线,第四列给出了预测模型的三个控制参数,第五列计算出了有效应力,上覆地层压力和地层压力,并给出了实测地层压力数据,可以看出后两者拟合的很好。由此可见,根据本发明实施例提出的干燥岩石弹性模量与有效应力的关系,进行地层压力预测与实测地层压力数据一致性很高,因此,本发明实施例提出的技术方案提高了地层压力预测的精确度。通过不断迭代,当利用理论关系计算出的弹性模量与利用测井曲线得到的弹性模量得到很好的拟合时,求得随深度变化的有效应力系数n。
另外,发明人发现传统预测地层压力的方法没有考虑岩性,因此,发明人考虑到了该关键问题,因此提出了将储层的砂、泥岩分开,在考虑孔隙度和泥质含量之后,分别计算砂、泥岩随深度变化的有效应力系数,再将数据整合在一起,其更加能精确的反映地层的实际情况,提供地层压力预测的精确度。下面对考虑岩性得到的砂、泥岩随深度变化的有效应力系数进行介绍如下。
在一个实施例中,上述步骤102中,根据干燥岩石弹性模量与有效应力的关系,以及研究区域内的测井数据,确定砂泥岩随深度变化的有效应力系数,可以包括:
对目标砂泥岩储层进行岩性划分,根据划分结果,将砂泥岩储层分为砂岩和泥岩;
根据砂岩弹性模量与有效应力的关系,确定砂岩随深度变化的砂岩有效应力系数;根据泥岩弹性模量与有效应力的关系,确定泥岩随深度变化的泥岩有效应力系数;
根据干燥岩石弹性模量与有效应力的关系,以及砂泥岩随深度变化的有效应力系数,对研究区域内单口井的所有待测目标层位进行地层压力预测,包括:
根据砂岩随深度变化的砂岩有效应力系数和泥岩随深度变化的泥岩有效应力系数,对研究区域内单口井的所有待测目标层位进行地层压力预测。
下面结合上述对目标砂泥岩储层进行岩性划分后得到的砂岩随深度变化的砂岩有效应力系数,以及泥岩随深度变化的泥岩有效应力系数,介绍上述步骤103中,单口井的所有待测目标层位进行地层压力计算的过程。
①单井分析:
上覆地层压力,即上覆所有岩石物质的重量产生的压力,因此只要对密度曲线数据进行一定的叠加处理,就可以获得上覆地层压力。根据如下公式,计算单井上覆地层压力梯度。
其中,Gob为上覆地层压梯度,ρm为缺失的密度,hm为缺失的深度,ρ为测井密度值,Δh为深度采样间隔,g为重力加速度,q为总离散点数。
利用上述公式(6)可以获得已有密度数据井段的上覆地层压力梯度数据,根据获得的梯度数据,结合下面的公式(7),可以拟合出缺失井段的上覆地层压力梯度数据。
Gob=a+bh-ce-dh; (7)
其中,h为深度,a,b,c,d为系数。根据上述公式(6)和(7),计算出上覆地层压力梯度,就可以换算出上覆地层压力值。
②三维地震分析:
地震资料求取上覆地层压力,本文是通过密度数据计算得到的。首先,是对地震数据进行叠前反演,获得三维密度数据体,针对三维密度数据体的每一道,缺失密度的部分按照公式(7)计算出每个深度的上覆地层压力梯度。然后按照以下公式(8),从密度数据体不为零的深度开始,取一定深度的采样间隔,依次对地层的压力进行相加:
其中,Po为上覆地层压力,hz为密度数据不为零时的深度,Gobz为深度hz处的上覆地层压力梯度,可根据上述公式(7)得到,ρ为某一深度的反演密度数据,Δh为采样间隔,其中,总离散点数q为:
其中,h为密度数据体的深度范围。
下面介绍对目标砂泥岩储层进行岩性划分后,得到的砂岩随深度变化的砂岩有效应力系数,以及泥岩随深度变化的泥岩有效应力系数的计算,本发明实施例利用Biot理论预测有效应力系数:
其中,n砂泥岩为有效应力系数,Ks为砂泥岩岩石骨架的体积模量,K0为砂泥岩骨架矿物的体积模量。
砂岩和泥岩骨架弹性模量,利用的是Krief模型,形式为:
Ksm=Ksand[1-C(h)][1-Φ(h)]1+C/[1-Φ(h)]; (11)
Kcm=KclayC(h)[1-Φ(h)]1+C/[1-Φ(h)]; (12)
其中,Ksm是砂岩骨架体积模量,μsm是砂岩骨架剪切模量,Kcm是泥岩骨架体积模量,μcm是泥岩骨架剪切模量,Ksand是砂岩骨架矿物体积模量,μsand是砂岩骨架矿物剪切模量,Kclay是泥岩骨架矿物体积模量,μclay是泥岩骨架矿物剪切模量,C(h)是深度h处的泥质含量,Φ(h)是深度h处的孔隙度,C是经验系数,Krief等人获得C的值为3,Goldberg和Gurevich得到C的值为2-4,Carcione等人使用C的值为2。C的值可以通过研究区域的当地数据来获得。
将公式(11)、(12)带入(10)中,可以分别获得考虑孔隙度和泥质含量的砂岩有效应力系数、泥岩有效应力系数,其计算公式分别如下公式(15)和(16)所示,上述公式(11)至(14)中各弹性模量参数都是当利用理论关系计算出的弹性模量与利用测井曲线得到的弹性模量得到很好的拟合时求得的,因此,利用这些弹性模量求得随深度变化的有效应力系数n也是精确度较高的,即为当利用理论关系计算出的弹性模量与利用测井曲线得到的弹性模量得到很好的拟合时的有效应力系数n。
在一个实施例中,根据砂岩弹性模量与有效应力的关系,确定砂岩随深度变化的砂岩有效应力系数,包括按照如下公式计算砂岩随深度变化的砂岩有效应力系数:
nsand=1-[1-C(h)][1-Φ(h)]1+C/[1-Φ(h)]; (15)
根据泥岩弹性模量与有效应力的关系,确定泥岩随深度变化的泥岩有效应力系数,包括:按照如下公式计算泥岩随深度变化的泥岩有效应力系数:
nclay=1-C(h)[1-Φ(h)]1+C/[1-Φ(h)]; (16)
其中,nsand为砂岩的有效应力系数,nclay为泥岩的有效应力系数,C(h)是深度h处的泥质含量,Φ(h)是深度h处的孔隙度,C是经验系数。
下面介绍上述步骤103中关于单口井地层压力的预测的详细步骤。
①上覆地层压力单井计算:根据公式(7),计算得到每口井上覆地层压力梯度数据。该梯度数据为已有密度井段的数值,根据该数值,再利用公式(8),得到连续梯度数据。我们可以根据得到的梯度数据,转换得到上覆地层压力数据。
②测井岩性参数计算:本文提出的地层压力预测模型,需要确定岩石各类矿物组分的含量及孔隙度。因此在本项发明中,采用最优化求解方法,得到研究区目的层段地层矿物组分变化曲线及孔隙度数据。
(a)、最优化测井解释原理:最优化测井解释方法利用超定线性方程组,在规定误差范围和约束条件的限定下,把每个矿物、流体等岩性参数的体积作为待求未知量,根据各种岩性参数的测井响应差异,利用各种测井曲线,在实测测井值与模型值误差最小的条件下,得到各种岩石成分。
(b)、建立的求解数学公式:
其中,Xi是第i个岩石成分体积含量,Ej是第j个测井曲线响应值,Dij是第i个岩石成分在第j个测井曲线上的响应值。
根据上述最优化测井解释方法,本发明挑选出研究区内LN1井做了计算和分析,分别获得单井的岩石参数曲线,包括无机矿物体积(石英、方解石),粘土矿物体积(高岭石、绿泥石和伊利石)和孔隙大小,计算实例见图6所示。从目的层段的岩石矿物上来看,其主要成分是石英和粘土,斜长石体积较小。粘土成分变化较大,主要成分是高岭石、伊利石、绿泥石,组成砂岩的主要矿物成分有石英、长石、方解石及白云石等。通过最优化测井解释,我们获得每口井的各种矿物含量和孔隙数据。其中粘土矿物含量为高岭石、伊利石、绿泥石之和,即泥质含量,孔隙度数据为单位体积1减去各种矿物含量剩余的数值。
③地层压力计算:上文中介绍了单井计算地层压力的方法,也叙述了单井数据的分析与处理,获得了计算地层压力的必要数据。利用获得的测井数据,结合地层压力的计算方法,就可以分别获得极限有效应力下的弹性模量Mlim、控制参数A、B、有效应力系数n,最后计算出地层压力,A为微裂隙密度因素,B为微裂隙闭合率因素。图7为研究区内LN1井的压力预测情况,对此口井的压力预测与分析可知,目的地层总体上压力正常,局部存在异常压力。
下面介绍上述步骤103中对研究区域进行三维地震地层压力预测的详细过程。
①上覆地层压力计算:利用上述的三维地震上覆地层压力计算方法,结合反演得到的密度数据体,得到研究区目的层段的上覆地层压力数据。
②地震资料岩性参数计算:上文介绍了单井计算地层压力的方法,由于单井获得的岩性参数数据较全面,在计算岩石弹性模量时,可以利用各种岩石成分含量。地震数据能够得到的地层岩性参数十分有限,通过叠前反演,只能获得目的地层的纵、横波速度数据和密度数据,因此在计算岩性参数时,需要进行粗化。本发明是利用纵、横波速度数据和密度数据,计算得到地层泥质含量和孔隙度数据,用泥质体积和非泥质部分体积代替各种矿物体积。
根据Castagna等人提出的速度经验公式:
Vp=a+b*Φ+c*Vsh; (18)
Vs=d+e*Φ+f*Vsh; (19)
其中,Φ是孔隙度大小,Vsh表示泥质含量大小,a、b、c、d、e、f是系数。
本发明反推泥质含量:
Vsh=G+H*Vp+I*Vs; (20)
利用公式(20)计算泥质含量时,首先利用单井数据,地层的纵、横波速度和密度数据进行回归分析,得到回归系数G、H、I。
如图8为砂泥岩地层泥质含量回归分析结果交会图,其中横坐标为单井计算的泥质含量数据,具体计算方法上文已经叙述,纵坐标为利用反推方程计算得到的泥质含量数据。图中结果显示,利用反推公式计算的泥质含量与测井值存在一定的指数关系。因此可以利用该反推公式,结合地震反演获得的纵、横波速度数据,获得泥质含量数据体。孔隙度是利用反演得到的密度数据和上文计算得到的泥质含量数据,根据如下公式计算得到的:
其中,ρb是测井密度值,ρf是孔隙流体密度值,ρma是岩石骨架密度值,ρsh为泥岩密度值。
利用上述孔隙度计算公式,结合上文计算得到的泥质含量数据,对孔隙度数据进行计算,如图9为孔隙度数据计算结果交会图。从图中可以看出,利用上述方程计算的孔隙度与测井计算值基本落在同一条直线上,预测误差在允许的范围内,可以用于地震数据来计算孔隙度。
我们利用测井数据约束地震参数的方法,通过地震反演得到泥质含量、孔隙度数据体,如图10、11所示。
③地震数据地层压力计算:为了获得地下三维的地层压力数据体,根据上文叙述的地层压力计算方法,将地层岩性分为泥岩和非泥岩部分,再结合孔隙度数据,得到地层岩石的极限有效应力下的弹性模量Mlim、控制参数A、B、有效应力和Biot系数等参数。利用上文介绍的预测新方法,进行了三维地层压力预测,为了更直观地体现本文预测方法较传统方法的不同,本文也利用Eaton方法进行了预测,其预测结果如图12所示。
通过对两种方法计算结果的比较,可以看出传统的Eaton方法由于只考虑纵波速度,其计算结果与纵波速度特征一致,大小特征按照层位特征排列十分严重。本发明研究方法计算的地层压力,消除了这一特征,其计算结果更加符合实际地层压力特征。利用已知的地层压力测量值,对两种计算结果进行验证,得出本研究方法计算的地层压力更加准确,精度更大,而传统的Eaton方法计算的结果,偏离实际值较大。本发明对传统方法进行了优化,因此精度更高。利用该方法,得到研究区三维地层压力,如图13所示。
基于同一发明构思,本发明实施例中还提供了一种砂泥岩储层地层压力的地震预测装置,如下面的实施例所述。由于一种砂泥岩储层地层压力的地震预测装置解决问题的原理与一种砂泥岩储层地层压力的地震预测方法相似,因此一种砂泥岩储层地层压力的地震预测装置的实施可以参见一种砂泥岩储层地层压力的地震预测方法的实施,重复之处不再赘述。以下所使用的,术语“单元”或者“模块”可以实现预定功能的软件和/或硬件的组合。尽管以下实施例所描述的装置较佳地以软件来实现,但是硬件,或者软件和硬件的组合的实现也是可能并被构想的。
图14是本发明实施例中砂泥岩储层地层压力的地震预测装置的结构示意图,如图14所示,该装置包括:
弹性模量与有效应力关系确定模块02,用于基于Hashin-Shtrikman边界模型,根据研究区域内目标砂泥岩储层的孔隙度和泥质含量,计算目标砂泥岩储层在极限有效应力下的弹性模量,微裂隙密度因素和微裂隙闭合率因素;根据极限有效应力下的弹性模量,微裂隙密度因素和微裂隙闭合率因素,确定干燥岩石弹性模量与有效应力的关系;
有效应力系数确定模块04,用于根据干燥岩石弹性模量与有效应力的关系,以及研究区域内的测井数据,确定砂泥岩随深度变化的有效应力系数;
地层压力预测模块06,用于根据干燥岩石弹性模量与有效应力的关系,以及砂泥岩随深度变化的有效应力系数,对研究区域内单口井的所有待测目标层位进行地层压力预测;根据干燥岩石弹性模量与有效应力的关系,以及有效应力系数,利用反演得到的弹性模量数据体,以单口井的地层压力为约束,对研究区域进行三维地震地层压力预测。
在一个实施例中,干燥岩石弹性模量与有效应力的关系为:
M=Mlim(1-A exp(-Pd/B));
其中,M为干燥岩石弹性模量,Pd为干燥样品压力变化和饱水岩石有效应力,Mlim为极限有效应力下的弹性模量,A为砂泥岩储层的微裂隙密度因素,B为砂泥岩储层的微裂隙闭合率因素。
显然,本领域的技术人员应该明白,上述的本发明实施例的各模块或各步骤可以用通用的计算装置来实现,它们可以集中在单个的计算装置上,或者分布在多个计算装置所组成的网络上,可选地,它们可以用计算装置可执行的程序代码来实现,从而,可以将它们存储在存储装置中由计算装置来执行,并且在某些情况下,可以以不同于此处的顺序执行所示出或描述的步骤,或者将它们分别制作成各个集成电路模块,或者将它们中的多个模块或步骤制作成单个集成电路模块来实现。这样,本发明实施例不限制于任何特定的硬件和软件结合。
以上所述仅为本发明的优选实施例而已,并不用于限制本发明,对于本领域的技术人员来说,本发明实施例可以有各种更改和变化。凡在本发明的精神和原则之内,所作的任何修改、等同替换、改进等,均应包含在本发明的保护范围之内。
- 还没有人留言评论。精彩留言会获得点赞!