一种用于室内无线定位的多误差模型的IMM算法的制作方法

本发明涉及无线定位网络
技术领域：
，尤其涉及一种用于室内无线定位的多误差模型的IMM算法。
背景技术：
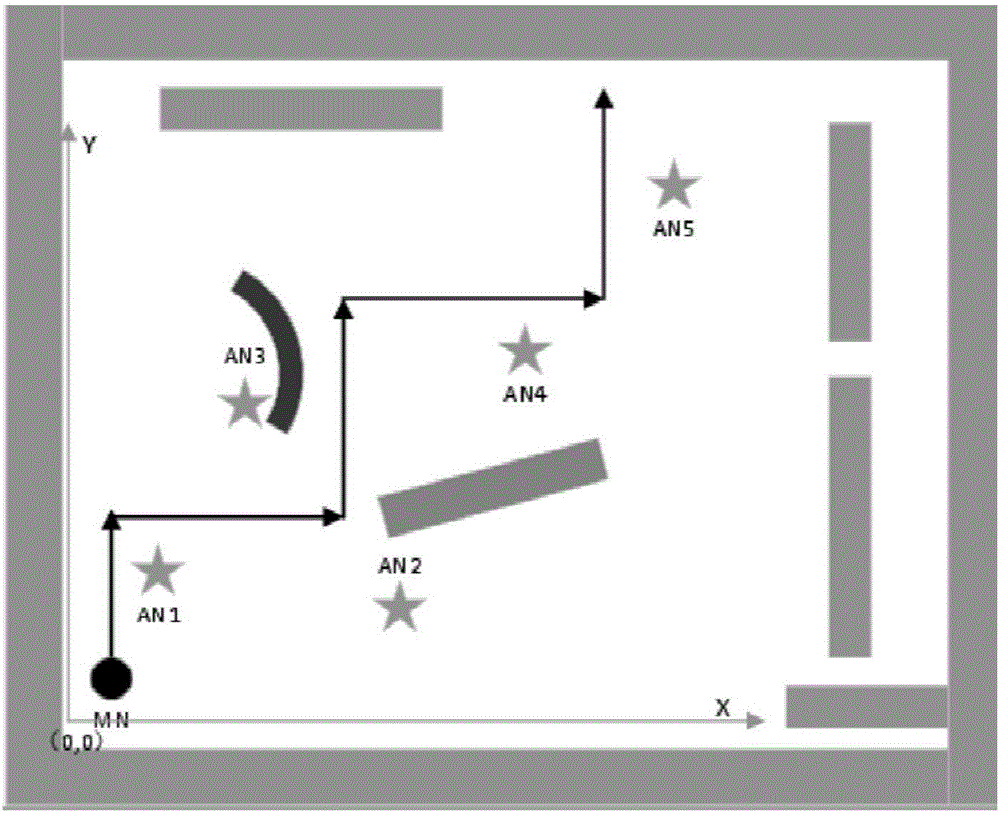
：目前使用最广泛的是GPS定位系统。但GPS由于建筑物的遮挡并不适合室内环境。然而，无线传感网络定位通过采用各种测距方式并结合已知位置的节点信息为室内定位提供了可能。作为一种全新的信息获取和处理技术，无线传感器网络在环境监测、目标跟踪等定位相关领域有着广泛的应用前景。确定事件发生的位置或获取信息的传感器节点的位置是无线传感器网络最基本的功能之一，没有位置信息的监测信息往往是毫无意义。无线传感器网络定位方法较多，目前最普遍的是根据是否需要测量距离进行划分:基于距离的定位算法(Range-Based)和距离无关的定位算法(Range-Free)。基于距离的定位算法包括基于信号传输时间(TOA)、基于信号传输时间差(TDOA)、基于信号到达角度(AOA)和基于接收信号强度指示(RSSI)等测量方法。基于RSSI的定位方法成本低，定位精度较高，但是在实际环境中容易受到反射、多径传播、天线增益、障碍物阻隔等因素的影响；尤其是障碍物的阻隔对RSS信号影响较大。因此如何消除由障碍物引起的误差一直是研究者们努力的方向。当目标节点(MN)在室内移动时，由于信号传播条件总是在视距和非视距间频繁转换。一种交互多模型的算法(InteractingMultipleModelIMM)被引入用来处理这种转换状态。经过众多研究者的仿真和实验证明这种算法机制优于一般的先鉴别非视距再消除非视距误差的方法。传统的IMM算法只是简单地将信号传播状态分为视距和非视距两种来进行处理。但通过实际测量，我们发现室内不同障碍物对非视距造成的误差差别较大。技术实现要素：本发明的目的在于提供一种多误差模型的IMM算法进一步消除由障碍物引起的误差。仿真结果和实验表明，采用本发明的多误差模型的IMM算法优于传统的单一误差模型算法。为达上述目的，本发明通过以下技术方案实现：一种多误差模型的IMM算法，用于目标节点MN的室内无线定位，所述MN和锚节点AN间的信道模型包括视距模型和非视距模型，其中，所述非视距模型按照室内环境信道状态统计结果分为3个不同的非视距模型；所述IMM算法分为四个阶段：输入交互，模型滤波，模型概率更新，输出交互；(1)输入交互输入交互过程是利用上一个循环得到的所有状态及模型条件概率为每个模型重新计算输入状态、输入状态误差协方差阵；首先计算模型交互概率：ck，j＝Σipijuk，i(n-1)其中，uk，i|j(n|n-1)表示第k个AN在时刻n-1，模型i的滤波结果在时刻n输入到模型j的转移概率；Pij为Markov链的模型转换概率，表示从模型i向模型j转换的概率；uk，i(n-1)为第k个AN在时刻n-1模型i的模型概率，ckj表示第K个锚节点的模型j的预测概率，是一个归一化变量；然后是协方差更新：其中，Pk，i(n-1|n-1)表示第i个模型在时刻n-1的后验概率，是包含初始测距值的初始状态估计，是模型i的混合状态估计；再计算时刻n模型j的输入值：是n时刻模型j的输入值信息，Markov链的模型转换概率为：并且满足p11+p12+p13+p14＝1，p21+p22+p23+p24＝1，p31+p32+p33+p34＝1，p41+p42+p43+p44＝1；(2)各模型滤波计算由于LOS与NLOS下测量噪声不同，采用4个不同的卡尔曼滤波器对测量距离进行滤波处理；(3)模型概率更新各模型进行滤波的同时需要计算模型似然和模型概率，假设模型似然服从高斯分布，则根据模型中观测和测量的残差得出模型似然：Λk，j(n)＝N(Vk，j(n)；0，Sk，j(n))其中，Sk，j(n)＝GPk，j(n|n-1)GT，G＝[10]，Λk，j(n)表示残差Vk，j(n)的均值为零，方差为Sk，j(n)的高斯密度函数，G是一个一行两列的矩阵，uk，j(n)＝1/ckΛk，j(n)ck，jckj表示第K个锚节点的模型j的预测概率。(4)输出交互最终的估计距离为进一步地，卡尔曼滤波算法分为2步：预测和更新；首先是基于卡尔曼滤波KF的预测过程：Pk，j(n|n-1)＝FdPk，0j(n|n-1)FdTFd是一个矩阵，Fd＝[1,T；0,1]然后是KF的测量更新Ka，k，j(n)＝Pk，j(n|n-1)GT[GPk，j(n|n-1)GT]-1Pk，j(n|n)＝[I-Ka，k，j(n)G]Pk，j(n|n-1)dkmes(n)是硬件模块测得的最初距离值，一般是一个包含测量噪声的值。本发明的有益效果是：本发明对于存在多种障碍物的复杂室内环境，引入多误差模型的IMM算法是一种有效消除误差的手段；多误差模型的IMM算法中的模型数与实际相匹配时，其算法的消除性能最佳，并且算法中模型数多于实际时的性能优于少于实际时的性能；引入多误差模型并不会增加IMM算法的复杂度，因此多误差模型的IMM算法是一种存在多种不同障碍物的室内环境下误差消除的有效方法。附图说明图1是目标节点和锚节点在室内环境中的分布图；图2是复杂室内环境信道状态统计示意图；图3是传统IMM算法框架图；图4是Markov链的转移概率示意图；图5是马尔可夫状态转移矩阵图；图6是实际环境存在4种不同障碍物模型；图7是实际环境存在5种不同误差模型。具体实施方案下面通过具体实施方式结合附图对本发明作进一步详细说明。本发明的系统模型如下：当MN在室内移动时，假设在时刻t，在MN与M个锚节点(AN)间的距离可表示为：其中，表示第m个AN和MN间的测量距离。附图1是MN的室内环境，附图2是其对应的信道条件。在时刻t，MN和第m个AN间的距离状态向量表示如下：Dm(t)＝[hm(t),Vm(t)]Tm＝1,2,3,…,M其中，hm(t)表示第m个AN和MN间的距离，Vm(t)表示MN的速度，M是AN的数量。MN的状态转移方程如下：Dm(t)＝FDm(t-1)+Cωd(t-1)其中，Ti表示采样时间间隔，ωd(t-1)表示独立同分布的高斯过程噪声。在每个t时刻MN的状态向量定义为：其中(x(t),y(t))表示MN在t时刻的坐标，表示MN在x和y方向的速度。MN的状态更新方程为：X(t)＝AX(t-1)+Bω(t-1)t＝1,2,3,…,TX(t-1)表示在t-1时刻的后验概率。其中，d(X(t))＝[d1(X(t)),d2(X(t)),…,dM(X(t))]T表示MN和AN间的欧氏距离；n(t)＝[n1(t),n2(t),…,nM(t)]T是距离测量噪声，其误差均值是μd，方差是根据不同的视距和非视距状态有：关于模型LOS、NLOS1、NLOS2、NLOS3，即是模型变量服从N(μ,σ2)的高斯分布，其中均值μ分别是0m，1.659m，4.048m，7.845m，对应的方差σ2分别为1.5747，1.76，3.0886，2.728。引入的模型数量过多会导致算法的复杂度过大，能适应实时定位快速测距定位的需求。因此，本发明根据实时定位跟踪过程中的需求，选取模型LOS、NLOS1、NLOS2、NLOS3。如附图3所示，传统IMM算法分为四个阶段：输入交互，模型滤波，模型概率更新，输出交互。IMM算法是一种递归算法。它的总体思想是通过不同的误差模型分别进行卡尔曼滤波进行优化处理。因此，依据这一思想尤其适合进行多误差模型的IMM扩展。(1)输入交互输入交互过程是利用上一个循环得到的所有状态及模型条件概率为每个模型重新计算输入状态、输入状态误差协方差阵。首先计算模型交互概率：ck，j＝Σipijuk，i(n-1)其中，uk，i|j(n|n-1)表示第k个AN在时刻n-1，模型i的滤波结果在时刻n输入到模型j的转移概率；Pij为Markov链的模型转换概率，表示从模型i向模型j转换的概率；uk，i(n-1)为第k个AN在时刻n-1模型i的模型概率，ckj表示第K个锚节点的模型j的预测概率，是一个归一化变量。然后是协方差更新：其中，Pk，i(n-1|n-1)表示第i个模型在时刻n-1的后验概率。再计算时刻n模型j的输入值：Markov链的模型转换概率如附图4所示：其中，P11+P12＝1，P21+P22＝1。(2)各模型滤波计算由于LOS与NLOS下测量噪声不同，采用2个不同的卡尔曼滤波器对测量距离进行滤波处理。卡尔曼滤波算法分为2步：预测和更新。首先是基于KF的预测过程：Pk,j(n|n-1)＝FdPk,0j(n|n-1)FdT然后是KF的测量更新Ka，k，j(n)＝Pk，j(n|n-1)GT[GPk，j(n|n-1)GT]-1Pk，j(n|n)＝[I-Ka，k，j(n)G]Pk，j(n|n-1)(3)模型概率更新各模型进行滤波的同时需要计算模型似然和模型概率，假设模型似然服从高斯分布，则根据模型中观测和测量的残差得出模型似然：Λk，j(n)＝N(Vk，j(n)；0，Sk，j(n))其中，Sk，j(n)＝GPk，j(n|n-1)GT，G＝[10]，Λk，j(n)表示残差Vk，j(n)的均值为零，方差为Sk，j(n)的高斯密度函数。uk，j(n)＝1/ckΛk，j(n)ck，j(4)输出交互最终的估计距离为本发明的多误差模型的IMM在传统IMM算法中，一般对两种状态进行滤波处理，一种是视距状态，一种是非视距状态。然而，这两种状态并不能充分描述实际室内环境中的信道情况。正如附图2所示，实际环境中存在多种不同的误差，所以本发明对模型状态进行了扩展。扩展后的马尔可夫状态转移矩阵表示如下图：其转移概率矩阵如下：并且满足p11+p12+p13+p14＝1，p21+p22+p23+p24＝1，p31+p32+p33+p34＝1，p41+p42+p43+p44＝1。接着进行仿真验证，本发明布置了5个位置已知的锚节点，MN在一个20m*35m的室内环境中移动，速度为0.5m/s，总长为50m。采样间隔为1s，采样总数为100。MN所处的环境和MN与各AN间的信道传播状态分别如附图1和附图2所示。附图5表示当室内环境实际存在4种不同的误差模型，分别用两模型的算法和4模型的算法对其进行误差消除的定位误差累积分布图。显然，使用多模型的算法优于两模型的算法。但是进行误差模型的扩展后也出现了新的问题，即在算法中如何采用误差模型才能有效消除非视距误差。因此，本发明首先统计了常见室内障碍物对信号的误差，如下表1。表1常见的室内障碍物对信号的噪声障碍物均值(m)方差视距(无障碍物)01.5747办公桌挡板1.6591.76玻璃门4.0483.0886人体7.8452.728桌椅家具9.7623.635墙11.935.7657从表1可知，不同障碍物对信号的噪声干扰差别很大。附图6已证明多误差模型在存在多种不同障碍物的环境中性能明显优于传统的两模型。因此，多误差模型的引入显得十分必要。为了进一步研究清楚多误差模型的IMM算法在处理复杂室内环境中的性能，本文进一步分析了多误差模型的IMM在实际环境中分别存在不同数量障碍物时的性能，如附图7所示。附图7描述了仅使用EKF、2至6种不同误差模型的IMM算法下处理实际环境中存在5种不同障碍物的定位误差累积分布图。从附图6可知，当IMM算法中的误差模型数正好和实际环境相匹配时，其误差消除的效果最优，如图中浅蓝色实线所示。再研究其他不匹配的情况发现，当IMM算法中使用的模型数与实际环境中相差越大，其误差消除效果越差。本发明研究发现了：①引入多误差模型的IMM算法有利于消除多障碍物的复杂环境的误差；②当多误差模型的IMM算法中的模型数与实际环境相匹配时，其误差消除效果最优。为了进一步研究多误差模型的IMM算法与实际环境中障碍物种类的关系，本文做了进一步分析，如表2所示。表2多误差模型的IMM算法与实际障碍物数量不同的定位误差统计表误差模型数二三四五六二4.24.85.45.66.7三9.86.36.86.96.6四12.111.47.57.67.8五15.712.611.27.28.1六17.814.912.611.210.8第一行表示的是在算法中使用的误差模型数，第一列表示的是实际的误差模型数。从表中可知，当两者误差模型数匹配时，其消除效果总是最佳的。当模型不匹配时，算法中模型数量多于实际情况会比少于实际模型情况好。表3描述了多误差模型的IMM算法中不同误差模型的算法复杂度。从表3中可看出，不同误差模型间复杂度并没有明显差别。因此，扩展IMM的误差模型并不会增加算法的复杂性。表3IMM不同模型数的算法复杂度模型数EKF二三四五六复杂度(s)0.2170.2860.3360.3930.4280.488综上所述，本发明对于存在多种障碍物的复杂室内环境，引入多误差模型的IMM算法是一种有效消除误差的手段；多误差模型的IMM算法中的模型数与实际相匹配时，其算法的消除性能最佳，并且算法中模型数多于实际时的性能优于少于实际时的性能；引入多误差模型并不会增加IMM算法的复杂度，因此多误差模型的IMM算法是一种存在多种不同障碍物的室内环境下误差消除的有效方法。以上内容是结合具体的优选实施方式对本发明所作的进一步详细说明，不能认定本发明的具体实施只局限于这些说明。对于本发明所属
技术领域：
的普通技术人员来说，在不脱离本发明构思的前提下，还可以做出若干简单推演或替换，都应当视为属于本发明的保护范围。当前第1页1 2 3