一种正四面体光纤光栅三维应变检测结构体的制作方法

本发明属于光纤光栅传感技术领域，特别涉及一种检测建筑体内部三维应变的光纤光栅结构体，该结构体由正四面体高弹性金属构件和六个布拉格光纤光栅组成，用于建筑体内部的三维应变检测。

背景技术：

光纤光栅是最近几年发展最为迅速的光纤无源器件之一，光纤光栅是利用光纤材料的光敏性，通过紫外曝光的方法将入射光相干场图样写入纤芯，在纤芯内产生沿纤芯轴向的折射率周期性变化，从而形成永久性空间的相位光栅，其作用实质上是在纤芯内形成一个窄带的(透射或反射)滤波器或反射镜。由于光栅光纤具有体积小、抗电磁干扰、检测精度高和易于埋入智能结构等优点，并且其谐振波长对温度、应变、折射率、浓度等外界环境的变化比较敏感，因此在光纤传感技术领域得到了广泛的应用。

物体的应变状态取决于材料的固有属性和所受到的应力状态。工程上常常需要根据应力应变等测试指标对材料的工作状态进行研究和评估。一般要确定建筑体内部的应变状态，需要用3个正应变和3个剪应变进行描述，即需要确定6个不同方向上的应变分量，亦即需要6个应变检测器件。从理论上讲，为确定三维应变状态，6个应变器件可以采用多种不同的三维应变花结构。

目前，建筑体内部的三维应变状态或应力状态常常是根据理论计算获得的。由于材料的不均匀性，理论计算往往误差较大。为了获得真实的应力和应变状态，有必要对受力体内部的应变状态进行直接检测。因此，建筑体内部三维应变状态的检测需要设计合理的应变检测结构。

技术实现要素：

本发明的目的在于检测建筑体内部的三维应变状态，设计一种光纤光栅应变检测结构体，能够对建筑体内部进行三维应变检测。

为实现上述目的，本发明采用如下技术方案：

一种正四面体光纤光栅三维应变检测结构体，由正四面体高弹性材料结构和六个三维布局的布拉格光纤光栅(FBG)组成。

高弹性材料结构，所述高弹性材料构件为正四面体，所述高弹性材料构件有六条棱，为30mm到50mm，截面宽度为2mm，高度为2mm，每条所述棱上都设置有安装槽；

布拉格光纤光栅，所述的布拉格光纤光栅有6个，所述的布拉格光纤光栅的特征波长不同，所述的布拉格光纤光栅固定在所述安装槽中。

所述的直角三棱锥光纤光栅结构体，所述的安装槽宽度为0.5mm，深度为1mm。

所述的直角三棱锥光纤光栅结构体，所述的布拉格光纤光栅采用环氧型胶黏剂固定在所述安装槽中。

附图说明

图1为本发明所述的正四面体高弹性结构体示意图。

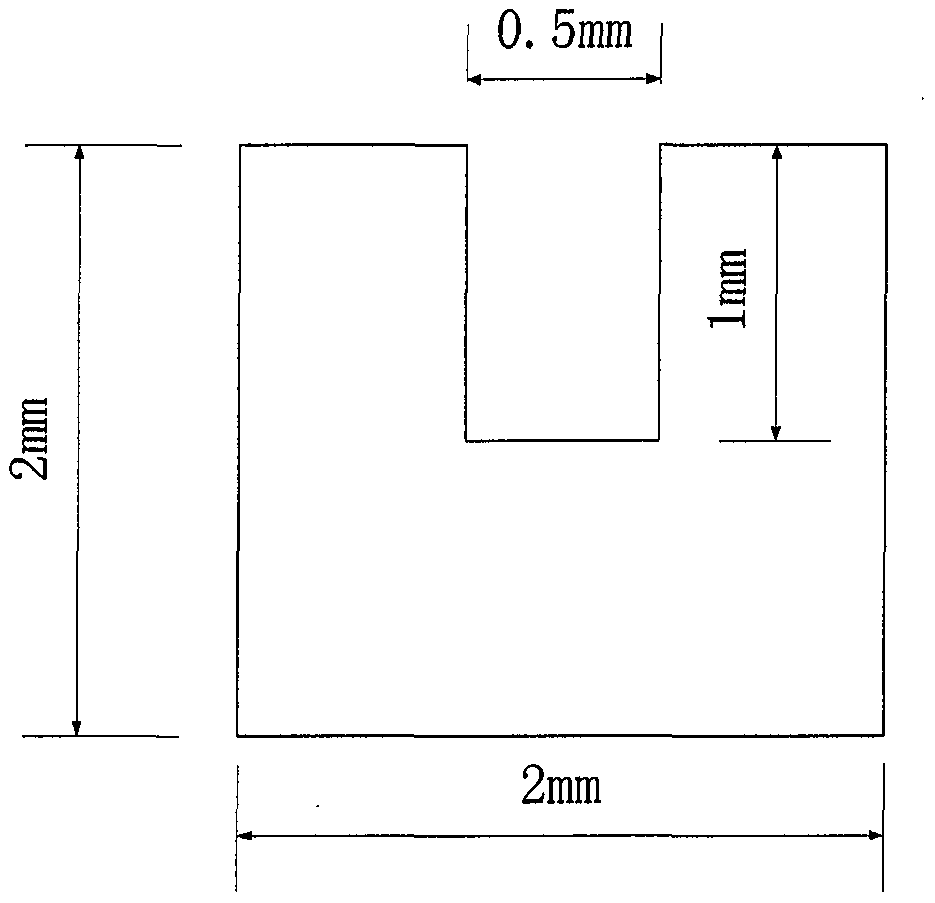
图2为本发明所述的正四面体高弹性结构体的棱的截面图。

具体实施方式

本发明是一种能对建筑体内部三维应变进行检测的正四面体高弹性结构体，下面将结合图1，对本发明作进一步说明。

用于三维应变检测光纤光栅结构体，由正四面体高弹性材料结构和六个三维布局的布拉格光纤光栅(FBG)组成。

所述的正四面体高弹性结构材料应选用高弹性和耐腐蚀的材料，可以采用不锈钢、铝合金或者弹性高分子材料。

所述的正四面体高弹性结构体OABC有六条棱OA、OB、OC、AC、BC和AB，如图1所示。

所述的棱OA、OB、OC、AC、BC和AB长度为30mm到50mm，棱的截面如图所示，截面宽度为2mm，高度为2mm，每条棱上开1mm深、0.5mm宽的光纤光栅安装槽。

所述的六根不同特征波长的布拉格光纤光栅使用环氧型胶黏剂(如Epo-tek353ND)固定在安装槽上，布拉格光纤光栅1、2、3分别固定在OA、OB、OC上，布拉格光纤光栅4、5、6分别固定在AB、BC、CA上。布拉格光纤光栅在进行固定时，须有适当的拉伸，以保证布拉格光纤光栅能检测构件的双向应变，在布拉格光纤固定在安装槽里之后用环氧型胶黏剂填充安装槽，以起到对布拉格光纤光栅的保护作用。

具体实施步骤如下：

步骤一：制作高弹性结构体

根据需要选择铝合金或者不锈钢等高弹性材料按照尺寸制作相应结构。并在高弹性材料结构的六个棱上刻一道0.5mm深、0.5mm宽的光纤光栅安装槽。

步骤二：固定布拉格光纤光栅

采用环氧型胶黏剂把六根不同特征波长的布拉格光纤光栅固定在光纤光栅安装槽中。

步骤三：通过填充环氧型胶黏剂的方式将光纤光栅固定在正四面体高弹性结构体的棱的内部起到保护光纤光栅的作用。

步骤四：将固定了光纤光栅的正四面体高弹性结构体埋入建筑体的内部，通过读取特征波长计算相应方向的线应变ε_i＝{ε₁，ε₂，ε₃，ε₄，ε₅，ε₆}，某点的一般应变状态可以从以下方法计算：

从一般情况考虑，三维空间中一条直线OA，该直线在xyz方向的方向角余弦1、m、n分别为：

n＝cosδ

式中：δ为直线与z轴的夹角；为直线在平面xOy的投影与x轴的夹角。若已知一点的应变状态为

ε_j＝{ε_xε_yε_zε_xyε_yzε_zx}

则OA方向的线应变为

ε＝ε_xl²+ε_ym²+ε_zn²+ε_zylm+ε_yzmn+ε_zxnl

亦即，如果知道一点的应变状态，则任意方向的线应变均可通过上式得到。相应的，若已知6个不同方向上的线应变，则常规应变状态也可以得到。设已知6个不同方向上的线应变分别为

式中i＝1，2，3，4，5，6。由常规应变状态到不同方向线应变的映射关系为

{ε_i}＝T{ε_j}

则{ε_j}＝T^-1{ε_i}

式中：j＝x，y，z，xy，yz，zx；ε_i＝{ε₁，ε₂，ε₃，ε₄，ε₅，ε₆}，根据正四面体方向余弦，可以求得

则

通过换算就可以得到建筑体内部某一点的常规应变状态。