利用波传播进行探测的方法和设备与流程

本发明涉及利用波传播进行探测的方法和设备。

背景技术：

利用波传播进行探测的方法采用传感器组件并且允许例如能够测量介质的特征参数以及/或者检测介质的奇异点以及/或者创建介质的图像。

这类方法尤其适用于检测和成像系统，例如，声纳、雷达、超声，等等。

在已知的这类方法中，尤其是在超声或雷达成像方法中，采用所捕获信号的简单散射分量：如果各个散射体仅只与波相互作用一次，那么每个回波的到达时间与传感器和产生该回波的散射体的分隔距离之间存在着有效的直接等效。回波在指定时刻的检测就意味着散射体存在于在与回波的到达时间相对应的距离上。然后，如有需要，就可以通过所接收到的信号来构建介质的反射性图像，也就是在介质内的各个散射体的位置。在超声或雷达成像方法中，并不太多地采用多重散射。这些成像方法往往是基于可以忽略多重散射的假设。

在存在着大量多重散射分量的情况下，尤其是在介质中所包含的散射体具有较高散射功率以及/或者在介质中非常密集的情况下，普通成像方法会受到严重的干扰并且不再是可靠的。实际上，在这种情况下，在回波的到达时间与传感器和介质散射体的分隔距离的之间不再有等效性性，这就难以构建出介质的图像。

专利申请书wo-2010/001027提出了一种能够将多重散射分量与简单散射分量相分离的探测方法。具体而言，该文件的方法包括以下步骤：

(a)发射步骤，在该步骤中，传感器组件(意即组件的某些或全部传感器)向介质中发射入射波，所述介质散射所述波，

(b)测量步骤，在该步骤中，所述传感器组件(意即组件的某些或全部传感器)捕捉表示反射波的信号，所述反射波是由介质对入射波的反射，所述捕获的信号包括：

-简单散射分量，表示是由介质的各个散射体单次反射入射波所形成的反射波的波路径，

-而且，在适当情况下，多重散射分量，表示是由介质的散射体上多次连续反射入射波在到达传感器组件之前所形成的反射波的波路径，

(c)处理步骤，在该步骤中，处理所捕获的信号，以便确定介质的特征(所讨论的特征可包括介质的图像，和/或介质的参数数值，和/或存在或者不存在比如多相性这样的奇异点，等等)，通过滤波至少一个频率变换矩阵，在多重散射分量与简单散射分量之中提取所选择的至少一个分量，所述频率变换矩阵表示在传感器组件的传感器之间的响应，并且至少包括下列子步骤：

(c1)确定窗口变换矩阵的子步骤，在该步骤中，确定与元件之间的响应(或者与在组件的传感器之间的响应)的窗口时间矩阵k(t，t)＝[kij(t，t)]相对应的至少一个窗口频率变换矩阵k(t，f)，所述元件之间响应的窗口时间矩阵在接近时间t和持续时间δt的时窗内与在传感器组件的传感器之间的时间响应hij(t)相对应，其中，f是频率，

(c2)数据旋转子步骤，在该步骤中，通过按照第一方向旋转以及从窗口频率变换矩阵提取分量，通过窗口频率变换矩阵k(t，f)来计算两个矩阵al(t，f)和a2(t，f)，

(c3)滤波子步骤，在该步骤中，将各个矩阵al、a2中的多重散射分量与简单散射分量相分离，由此得到至少两个滤波矩阵a1^f、a2^f，所述两个滤波矩阵分别与矩阵al、a2相对应并且分别表示简单散射分量或者多重散射分量，

(c4)反向数据旋转子步骤，在该步骤中，通过按照与第一方向相反的第二方向旋转以及从滤波矩阵a1^f、a2^f中提取分量，通过两个滤波矩阵a1^f、a2^f来计算滤波窗口变换矩阵k^f(t，f)。

技术实现要素：

本发明的目的旨在精炼和改善上述探测方法。

为此目的，根据本发明的方法的处理步骤使得：

-在数据旋转步骤(c2)中，窗口频率变换矩阵k(t，f)的所有分量分布在两个矩阵al(t，f)和a2(t，f)中的一个或另一个矩阵的中心部位，这些矩阵所具有的零点在中心部位之外的部分，以及，

-在反向数据旋转步骤(c4)中，提取滤波矩阵a1^f、a2^f的中心部位的所有非零分量并将其放置在滤波窗口变换矩阵k^f(t，f)之中。

通过根据本发明的方法的这些特征，可以在处理步骤中考虑来自介质的更大量信息。因此，利用波传播来探测介质也就更为有效，并且使之能够探测到介质的更大深度。

此外，由此所产生的介质图像的空间分辨率可以更高。因此，有可能使用具有较少数量传感器的传感器组件，使得该方法的成本较低。

此外，例如，分量的分离使之能够：

-仅仅只利用简单的散射分量来构建介质的图像，或者，

-通过多重散射分量来确定介质的特征参数，或者，

-确定很少有或者没有多重散射，以此表述介质的特征。

在根据本发明的方法的各个实施例中，有可能采用下列设置中的一项或多项。

根据方法的一方面，窗口变换矩阵k(t，f)是尺寸为nxn的矩阵，其中，n是奇数，而且在数据旋转步骤(c2)中，两个矩阵a1(t，f)＝[a1uv(t，f)]和a2＝[a2uv(t，f)]可以通过窗口频率变换矩阵k(t，f)＝[kij(t，f)]按照下列关系来计算：

-如果u+v-1-(n-1)/2和v-u+(n+3)/2-1都在1与n之间且包含1和n，

那么a1uv(t，f)＝ku+v-1-(n-1)/2，v-u+(n+3)/2-1(t，f)，

否则a1uv(t，f)＝0，并且，

-如果u+v-(n-1)/2和v-u+(n+3)/2-1都在1与n-1之间且包含1和n-1，

那么a2uv(t，f)＝ku+v-(n-1)/2，v-u+(n+3)/2-1(t，f)，

否则a2uv(t，f)＝0。

根据方法的一方面，数据旋转子步骤(c2)包括：

-第一个子步骤(c21)，在该子步骤中，将窗口频率变换矩阵k(t，f)引入尺寸更大的广义矩阵ke(t，f)中，除了来自窗口频率变换矩阵的元素之外，广义矩阵的所有元素都为零，以及，

-第二个子步骤(c22)，在该子步骤中，两个矩阵al(t，f)和a2(t，f)可以通过广义矩阵ke(t，f)来计算。

根据方法的一方面，窗口变换矩阵k(t，f)是尺寸为nxn的矩阵，其中，n是奇数，而且：

-在第一个子步骤(c21)中，广义矩阵ke(t，f)＝[keij(t，f)]定义如下：

如果i∈[1+(n-1)/2；n+(n-1)/2]，以及，

j∈[1+(n-1)/2；n+(n-1)/2]

那么keij(t，f)＝ki-(n-1)/2，j-(n-1)/2(t，f)，

否则keij(t，f)＝0，以及，

-在第二个子步骤(c22)中，两个矩阵a1(t，f)＝[a1uv(t，f)]，a2(t，f)＝[a2uv(t，f)]可通过下列关系来计算：

a1uv(t，f)＝keu+v-1，v-u+(n+3)/2-1+(n-1)/2(t，f)，以及，

a2uv(t，f)＝keu+v，v-u+(n+3)/2-1+(n-1)/2(t，f)。

根据方法的一方面，窗口变换矩阵k(t，f)是尺寸为nxn的矩阵，其中，n是奇数，而且在反向数据旋转步骤(c4)中，滤波窗口变换矩阵k^f(t，f)＝[k^fij(t，f)]可通过滤波矩阵a1^f(t，f)＝[a1^fuv(t，f)]，a2^f(t，f)＝[a2^fuv(t，f)]按照下列关系来计算：

如果i-j是偶数，

那么k^fij(t，f)＝a1^f(i-j)/2+(n+1)/2，(i+j)/2，

否则k^fij(t，f)＝a2^f(i-j-1)/2+(n+1)/2，(i+j-1)/2。

根据方法的一方面，在确定窗口变换矩阵的子步骤(cl)中，通过窗口时间矩阵k(t，t)的小波变换来确定各个窗口频率变换矩阵k(t，f)，所述窗口时间矩阵k(t，t)在接近时间t和持续时间δt的所述时窗内与在传感器组件的传感器之间的时间响应hij(t)相对应。

根据方法的一方面，各个窗口变换矩阵k(t，f)的时窗至少成对地重叠。

根据方法的一方面，在滤波子步骤(c3)中：

-从矩阵k(t，f)的各个系数kij(t，f)中提取简单散射分量k^sij(t，f)，以便简单散射分量sk^sij(t，f)在所述矩阵k(t，f)的各个反对角相互相关，而且，

-从矩阵k(t，f)的各个系数kij(t，f)中提取多重散射分量k^mij(t，f)。

根据方法的一方面，在发射步骤中，发射进入介质中的入射波以预定的角度朝所述介质的外表面倾斜。

本发明还涉及实施上述探测方法的设备，包括传感器组件，适合向散射介质中发射入射波并且捕获表示反射波的信号，所述反射波是由介质反射入射波所形成的，所述捕获的信号包括：

-简单散射分量，表示反射波是由介质中的各个散射体单次反射入射波所形成的波路径，

-以及，在适当情况下，多重散射分量，表示反射波是由介质的散射体上多次连续反射入射波在到达传感器组件之前所形成反射波的波路径，

所述设备进一步包括处理装置，适合处理所述捕获的信号，以便确定介质的特征，

处理装置适合通过至少一个频率变换矩阵的滤波，从多重散射分量和简单散射分量中提取所选择的至少一个分量，所述频率变换矩阵表示在传感器组件的传感器之间的响应，并且处理装置至少执行以下子步骤：

(c1)确定窗口变换矩阵的子步骤，在该步骤中，确定与元件之间响应的窗口时间矩阵k(t，t)＝[kij(t，t)]相对应的至少一个窗口频率变换矩阵k(t，f)，所述元件之间响应的窗口时间矩阵在接近时间t和持续时间δt的时窗内与在传感器组件的传感器之间的时间响应hij(t)相对应，其中，f是频率，

(c2)数据旋转子步骤，在该步骤中，通过按照第一方向旋转并且从窗口频率变换矩阵中提取分量，通过窗口频率变换矩阵k(t，f)来计算两个矩阵al(t，f)和a2(t，f)，

(c3)滤波子步骤，在该步骤中，将各个矩阵al、a2中的多重散射分量与简单散射分量相分离，由此得到至少两个滤波矩阵a1^f、a2^f，所述两个滤波矩阵分别与矩阵al、a2相对应并且分别表示简单散射分量或者多重散射分量，

(c4)反向数据旋转子步骤，在该步骤中，通过按照与第一方向相反的第二方向旋转并且从滤波矩阵a1^f、a2^f中提取分量，通过两个滤波矩阵a1^f、a2^f来计算滤波窗口变换矩阵k^f(t，f)。

本发明的设备使得处理装置适合于：

-在数据旋转步骤(c2)中，窗口频率变换矩阵k(t，f)的所有分量都分布在两个矩阵al(t，f)和a2(t，f)中的一个或另一个矩阵的中心部位，这些矩阵所具有的零点在中心部位之外的部分，以及，

-在反向数据旋转步骤(c4)中，提取滤波矩阵a1^f、a2^f的中心部位的所有非零分量并将其放置在滤波窗口变换矩阵k^f(t，f)之中。

附图说明

通过以非限制性实例的方式列出的本发明实施例的以下说明，参考附图，本发明的其它特征和优点显而易见。

在附图中：

-图1是实施根据本发明实施例的方法的设备的示意图，

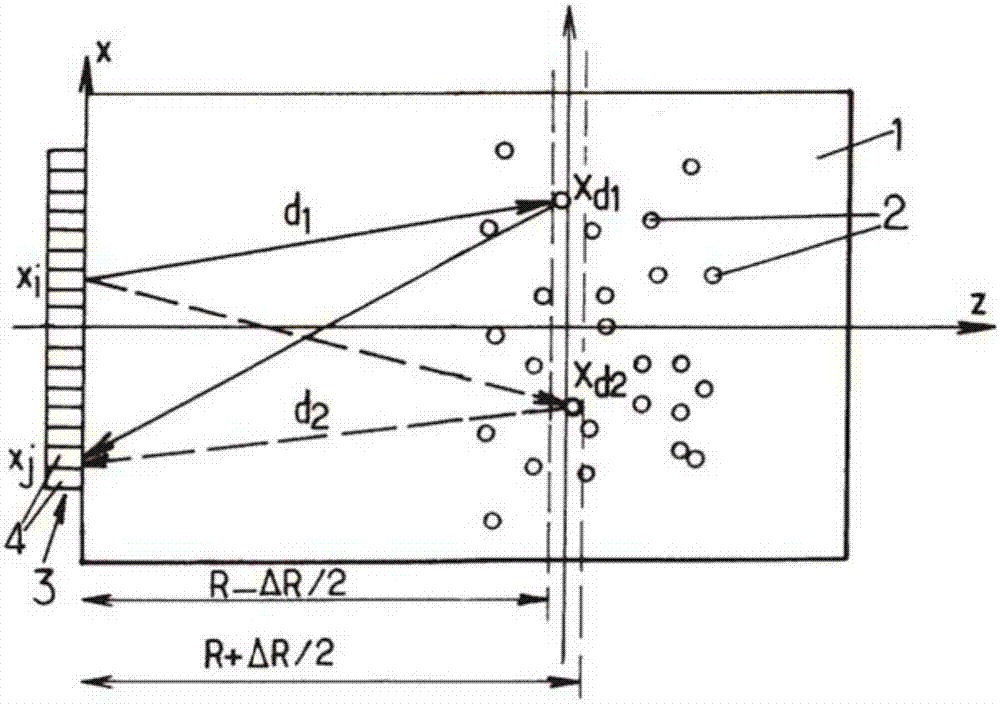
-图2是展示了两个简单散射路径的图表，在图1所示的实例中，所述简单散射路径有助于形成探测介质在时间t＝2r/c反向散射的场，

-图3是展示了两个多重散射路径的图表，在图1所示的实例中，所述多重散射路径有助于形成探测介质在时间t＝2r/c反向散射的场，

-图4和图5阐释了数据旋转子步骤，所述数据旋转子步骤是根据现有技术方法的实施例的一部分，其中，从各个窗口频率变换矩阵k中提取两个矩阵a1和a2，

-图6阐释了反向数据旋转子步骤，在该子步骤中，对所述矩阵滤波之后，通过上述矩阵al和a2来确定滤波变换矩阵k^f，

-图7阐释了滤波阵列al和a2通过奇异值分解的迭代过程，

-图8阐释了根据本发明第一个实施例的示例性广义矩阵ke，

-图9和图10显示了通过图8的第一个实施例的广义矩阵所获得的或者根据本发明第二个实施例从窗口频率变换矩阵k所直接获得的两个矩阵al和a2，

-图11a、图l1b和图11c阐释了在本发明的方法中可用于形成窗口频率变换矩阵k的母小波函数的三个实例，以及

-图12是设备的变体的示意图，具有相对于介质外表面倾斜并且适合实施根据本发明方法的实施例的多个传感器。

具体实施方式

图1显示了适合通过发射和接收波来探测介质1的设备的一个实例。在下文中，本发明针对所讨论的波为超声波(例如，频率为2mhz至4mhz)的情况作更具体的说明，当然，本发明也适合任何类型的波，例如，除超声压缩波以外的机械波、电磁波或其它波。

介质1是所讨论的波的散射介质，意即所述介质是均质的以及/或者包含随机分布的散射体2，并且所述散射体能够反射发射入介质1中的波。

所讨论的介质1可以是，例如人体的一部分，而散射体2可以是包含在介质1中的未溶解的小颗粒(这种散射体会在超声中产生“散斑”图像)。当然，待探测的介质1可以是其它介质，例如，工业项目中的一部分，有待于在非破坏性试验的环境下对其结构进行测试。

图1所示的探测设备包括传感器4的组件3，例如，超声传感器的线性阵列，其典型的形式通常为与介质1相接触的刚性阵列。该组件3包括n个传感器，例如，n介于100至500之间。例如，可以采用一百个传感器4的阵列，每个传感器的宽度约为0.39毫米。值得注意的是，传感器4在此为超声传感器，它能够将电气信号转换为超声压缩波，反之亦然，但是就本专利的意义而言，传感器更普遍地是指能够将电气信号转换为某个类型的波(机械波、电磁波等)并且反之亦然的任何设备。

组件3的各个传感器4可以由中央处理器5(uc)单独控制，例如，所述中央处理器包括数字信号处理装置，该中央处理器5能够例如在屏幕6上显示介质1的图像。

为了探测介质1，中央处理器5向传感器4发送电气信号，通过所述传感器将所述电气信号转换为发射入介质2中的波，在这种情况下，为超声压缩波并且这些波由介质中包含的散射体2局部反射。一部分散射波(或回波)因此返回传感器4，所述传感器捕获并将其转换为电气接收信号，随后由中央处理器5对其进行处理。

这些波返回传感器4：

-或者，经散射体2反射一次之后(例如，沿着图1的虚线按照图示所示的路径)，换言之，在简单散射之后，

-或者，经过多个散射体2连续反射之后(例如，沿着图1的实线按照图示所示的路径)，换言之，在多重散射之后。

经介质1散射并返回传感器4的整体波因此包括两个作用：

-“简单散射”作用，与入射波在回到传感器4之前仅经过介质1各个散射体1的单次反射的情况相对应，

-“多重散射”作用，与入射波在到达传感器4之前经过在介质散射体2上的多次连续反射的情况相对应。

这种方法能够通过滤波将这两个作用相分离，所以只采用其中一个，或者分别对其进行处理。例如：

-简单散射作用有助于构建介质的图像，尤其是在此所述的情况下通过超声来构建介质的图像(但是，在地震波的情况下，可以是震波的图像，或者在电磁波的情况下，可以是雷达的图像，或者为其它的图像)：事实上，因为各个散射体2仅仅只与入射波相互作用一次，所以每个回波的到达时间与在传感器和产生该回波的散射体之间的距离之间有效地直接等效。以指定时间来检测回波信号可以表示在与回波的到达时间相对应的距离存在着散射体2。然后，可以通过记录的信号来构建介质反射性的图像，意即介质内各个散射中心的位置；

-多重散射作用还有助于表述无序介质的特征，因为它能够测量统计参数，例如平均畅通路径或者通过随机介质传播的波的散射系数；这种多重散射作用的相对重要性使之能够表述例如通过超声所获得的介质1图像的可靠性的特征。

为了把简单散射作用与多重散射作用相分离，首先记录组件3的各对传感器4的元件之间的响应。

为此目的，如图2所示，在发射步骤(a)中，由组件3的第i个传感器(横坐标xi)发送与脉冲信号相对应的入射波，并且在测量步骤(b)中，由第j个传感器(横坐标xj)记录在发射入射波之后由介质背向散射(反射)的波。在这个操作过程中，各个传感器j捕获在传感器i发射之后的时间信号hij(t)。该操作适合于组件3的所有可能存在的发射器/接收器对，意即实际上适合于传感器4的所有对进行该操作。

n²个响应的集构建元件之间响应的时间矩阵h(t)＝[hij(t)]，即尺寸为nxn的矩形矩阵，这是介质1的整体响应。注意，例如，通过文件wo-a-2004/086557所描述的程序，有可能更迅速地获取元件之间响应的时间矩阵h(t)，而无需组件3的各个传感器i连续发射脉冲信号。

信号hij(t)通过中央处理器5进行数字化(例如，按照9位或相类似)，采样(例如，例如针对超声波以20mhz的频率进行采样)，以及储存。

中央处理器5然后执行处理步骤(c)，包括确定窗口变换矩阵的初始子步骤(c1)。

在该子步骤(c1)中，首先是将各个脉冲响应hij(t)缩短(窗口)为持续时间δt的连续时窗。

由此得到尺寸为nxn的一系列窗口时间矩阵k(t，t)＝[kij(t，t)]，其中，kij(t，t)是与时窗[t-δt/2窗口时；t+δt/2窗口]相对应的hij(t)的贡献，为：

kij(t,t)＝hij(t)×wr(t-t)(1)

使得：

-若t∈[-δt/2；+δt/2]，则wr(t)＝1，否则wr(t)＝0，

-r＝c.t/2是沿着z轴从传感器组件3测量的距离(见图2)，所述z轴垂直于所述传感器组件的纵向x(在此所考虑的实例中构成线性阵列)，

-c是波在介质1中的速度(在超声的具体情况下，为在水中或在人体的软组织中，c＝1.5mm/μs)，

-δt是预定的持续时间，对应于在上述时间间隔[t-δt/2时；t+δt/2]内波所行进的距离δr＝c.δt，有利的是，这是连续的，意即其完全包括所确定的时间段(换言之，所进行的处理包括视野深度，意即也是连续的r的一系列值)。

在子步骤(c1)中，进行矩阵k(t，t)系数的离散傅里叶变换，从而获得尺寸为nxn的变换矩阵的t的各个数值，所述变换矩阵也称之为窗口频率变换矩阵k(t，f)＝[kij(t，f)]，其中，kij(t，f)是kij(t，t)的离散傅里叶变换以及f是其频率。

根据这些窗口频率变换矩阵k(t，f)，在随后的滤波子步骤(c3)中，可以通过滤波将简单散射作用和多重散射的作用相分离，所述随后的滤波子步骤(c3)是处理步骤(c)的一部分。

具体的说，在该随后的滤波子步骤(c3)中，可以基于所述窗口频率变换矩阵k(t，f)的各个反对角上的窗口频域变换矩阵k(t，f)的系数kij(t，f)的相干性将各个窗口频率变换矩阵k(t，f)中的多重散射分量和简单散射分量相分离(反对角常称之为所述矩阵的系数kij(t，f)队列，以便i+j是常量)窗口。

实际上，简单散射波沿着矩阵k(t，f)的反对角具有明显的相干性，而多重散射波具有随机性且在所述矩阵k(t，f)不呈现出优选的相干方向。通过仔细滤波这些反对角，可以把两个作用相分离。

该特性可作如下解释。

各个脉冲响应hij(t)可分解为以下形式：

其中，和分别与来自简单散射(s)和多重散射(m)的信号相对应。

同样，窗口频率变换矩阵k(t，f)的系数kij(t,f)可分别分解为的形式，其中，是简单散射的作用，是多重散射的作用。

可将各个作用视为与多个简单散射路径相关的分波的总和，其两个实例(路径d1和路径d2)如图2所示。在时窗[t-δt/2；t+δt/2-]内，可以到达传感器阵列的简单散射波与初始波对在位于厚度为δr＝c.δt、深度为r＝ct/2的介质区域内的散射体的反射相对应。

我们用术语“等体积”表示一组点，这组点在指定时刻t有助于在阵列中所捕获的信号。实际上，等体积并不全是与阵列表面平行的部分，而是由椭圆叠加产生的，所述椭圆的焦点是发射器元素(i)和接收器元素(j)。在远场中，意即在r足够大的情况下，等体积相似于平行于阵列且与其距离为r＝ct/2的厚度为δr的部分。

在元素i和j之间的响应可以分解为通过在等体积的nd个散射体上反射产生的分波的总和。采用两维方式，在近轴近似的情况下，我们可以把写为：

其中，整数d表示有助于在时间t所接收到的信号的第d^th个简单散射路径，xd是散射体d(沿着轴x)的横向位置，k是周围介质中的波数(k＝2πλ，λ是波长)，以及ad是表述散射体d反射性特征的振幅。

值得注意的是，在上述等式(3)中以及在当前专利申请书的其它等式中，j是虚数，所以在不作为下标的情况下，j²＝-1，但是在作为下标的情况下，则表示矩阵元素的位置。

多重散射的作用还可以分解为与多重散射路径相对应的分波，所述多重散射路径的长度在区间[r-δr/2；r+δr/2]内，如图3(针对指数p和q的两个路径)所示。

我们可以把写为：

其中，整数p表示所涉及的多重散射路径的指数。在图3所示的实例中，对子和分别表示路径p的第一个和最后一个散射体的坐标。bp相当于与路径p相关的分波的复振幅，从第一个散射事件到最后一个散射事件

尽管散射体2在介质1中的分布是完全随机的而且在散射体之间没有关联，但是与简单散射相关的信号却有特殊的相干性，这与多重散射的作用不同。实际上，等式(3)可以写为：

在等式(5)之和的前面所出现的项与散射体的精确分布无关，并因此起着决定性的作用，表述了简单散射的特征。右边的项是随机的，因为它明确地取决于散射体的位置。

相比之下，与多重散射相关的信号(等式4)就不能这样来写成。

源自简单散射的信号的该特性可以表达为沿着各个矩阵k(t，f)的反对角的特殊相干性，如图4所示。实际上，沿着各个反对角，意即针对发射器(i)/接收器(j)对，其中，i+j＝常数，的随机作用是常数。对于指定的散射介质而言，在简单散射中，因此位于相同反对角上的各个矩阵k(t，f)的系数之间存在确定性的相位关系。

然而，在多重散射中，则不再满足这个特性，而且矩阵k(t，f)不具有特殊的相干性：元素不受彼此影响。

本方法利用了这个特性，以便在用实验方法测量的信号的基础上，利用各个矩阵k(t，f)内的简单散射作用的特殊对称性，通过滤波就能将简单散射作用与多重散射作用相分离。因此，可以过滤掉：

-矩阵k(t，f)的各个系数kij(t，f)的简单散射分量k^sij(t，f)，使得简单散射分量sk^sij(t，f)在所述矩阵k(t，f)的各个反对角相互相干，

-以及矩阵k(t，f)的各个系数kij(t，f)的多重散射分量k^mij(t，f)，所以分量k^mij(t，f)是随机的且彼此不关联。

适用于分离两种作用的两种示例性滤波技术如下文所述。

按照这两种技术，在确定窗口变换矩阵的子步骤(c1)之后，处理步骤(c)包括以下两个子步骤：

-数据旋转子步骤(c2)，通过旋转各个矩阵k(t，f)的数据并构建两个子阵a1(t，f)和a2(t，f)，

-上文提及的滤波子步骤(c3)，在该子步骤中，对矩阵a1和a2进行滤波，尤其是通过投影(技术1)或者通过奇异值分解(技术2)，由此可以得到两个滤波矩阵，表示为和

-反向数据旋转子步骤(c4)，由此使之能够通过和重新构建包含简单散射的作用或者多重散射的作用的滤波变换矩阵k^f(t，f)，这取决于所应用的滤波的类型。

下面详细说明了这些子步骤(c2)至(c4)。

子步骤(c2)：数据旋转

在该子步骤(c2)中，中央处理器5通过各个矩阵k(t，f)来计算两个矩阵a1(t，f)＝[a1uv(t，f)]和a2＝[a2uv(t，f)]，

其中：

a1uv(t，f)＝ku+v-1，v-u+2m-1(t，f)，

a2uv(t，f)＝ku+v，v-u+2m-1(t，f)，

m＝(n+3)/4。

选择n，使得m为整数：例如，n＝125和m＝32。如果传感器3的总数使得m不是整数，我们通过减少的数量n个传感器进行计算，使得m＝(n+3)/4为整数(在此所考虑的具体实例中，例如，我们可以利用128个传感器的阵列且仅仅只采用n＝125进行计算)。

矩阵a1和a2是由按照逆时针方向旋转45°的矩阵k(t，f)的子集所构建的矩形矩阵。图4和图5分别阐释了这些矩阵a1和a2，可将其理解如下：

-a1是尺寸为(2m-1)×(2m-1)的矩形矩阵，其中，各行由矩阵k(t，f)中的某些对角线(每隔一个)所构成，包括在图4中圈出的矩阵k(t，f)的系数(k(t，f)的系数在图4和图5中用点表示)，

-a2是尺寸为(2m-2)×(2m-2)的矩形矩阵，其中，各行由矩阵k(t，f)中的其它对角线所构成，包括在图5中圈出的矩阵k(t，f)的系数。

在下文中，我们可以用ar＝[arij]来表示矩阵a1和a2(r＝1或2)，而且我们用l表示矩阵ar的尺寸(关于矩阵a1，我们因此得到l＝2m-1，关于矩阵a2，得到l＝2m-2)。

由于空间的相互作用，矩阵k相对于其主对角线d(kij＝kji)对称。矩阵ar因此也具有对称性：其上部每一行与其下部的一行相同，相对于与主对角线d相对应的水平中心线对称。因此，通过下部就可以直接推断出矩阵ar的上部。于是，矩阵a1的各列仅仅只包括m个独立系数，只要其尺寸l>m，以及矩阵a2的各列包括m-1个独立系数。更普遍而言，矩阵ar的独立系数的数量因此为数量mr，使得如果r＝1，则mr＝m；如果r＝2，则mr＝m-1。

子步骤(c3)：滤波

在滤波子步骤(c3)中，中央处理器5将各个矩阵ar中的多重散射分量与简单散射分量相分离，r是等于1或2的指数，因此我们得到至少两个滤波矩阵ar^f，分别与两个矩阵ar相对应并且分别表示简单散射分量或多重散射分量。

尤其是，该滤波可以根据上文所提及的技术1或者根据技术2进行。

1.技术1：投影滤波

按照这第一种技术，在滤波子步骤(c3)中，中央处理器5计算分别表示简单散射的两个滤波矩阵ar^f。

通过下列公式来计算各个所述滤波矩阵：

ar^f＝s^ts^*ar，

其中：

-s＝[su]是列向量，^ts*是向量s的共轭向量的转置阵列，

-向量s的分量su是复数，等于：

-s是常数，实际上等于1(因此下文未提及)，

-其中，如果r＝1，则u＝(i-j)/2+m，如果r＝2，则u＝(i-j-1)/2+m，

-xi和xj是沿着轴x的指数i和j的传感器的横坐标，传感器组件至少沿着所述轴x延伸，

-若r＝1则l＝2m-1，若r＝2则l＝2m-2。

该公式调整如下。

各个矩阵ar为两项之和，即ar^s和ar^m，分别表示简单散射和多重散射的作用：

ar＝ar^s+ar^m(6)

数据旋转，换言之，从k(t，f)变换到ar，在数学上表达为坐标变换(xi，xj)→(yu，yv)：

和

然后，根据该新基础把等式(5)写为：

其中，

因此，对于指定介质1而言，矩阵ar^s的各列都完全确定地取决于各列的指数(u)。

然而，不能对多重散射的作用(等式4)进行如此简单的因式分解。即使在旋转矩阵之后，散射体的位置的随机性仍存在于矩阵ar^m的各列和各行。

因此，通过将整个矩阵ar的各列投影到由坐标向量s所产生的“简单散射的特征空间”中，就可以对简单散射信号进行滤波：

分母中存在确保向量s的归一化。通过如此投影所产生的行向量p可写为：

p＝^ts^*ar(9)，

其中，^ts^*是向量s的共轭转置阵列。

矢量p的坐标可由下式给出：

剩余项与向量s上的多重散射信号的投影相对应。

然后，用列向量s乘以行向量p得到滤波矩阵ar^f：

ar^f＝sp＝s.^ts^*.a(11)

于是，把矩阵ar^f的坐标写为：

第一项直接等于简单散射分量(等式7)。因此，我们得到：

就矩阵而言，等式(13)写为：

矩阵ar^f实际上并不包含与简单散射(a^s)相关的作用，还包含与多重散射(s^ts^*a^m)的存在相关的剩余项。该项的存留是因为多重散射信号并非直接与通过向量s所产生的简单散射的特征空间相正交。

所获得的滤波因此并不完美；然而可以评估残留噪声的程度。

实际上，如涉及数据旋转的段落所述，矩阵a1中的各列都仅仅只有m个独立的系数，矩阵a2中仅仅只有m-1个独立系数；因此，多重散射的作用经滤波之后减少了因子由于简单散射的作用保持不变，所以，信噪比，或更具体而言，“简单散射/多重散射”比与相似。

上述滤波技术(技术1)尤其适用于想要提取被多重散射所遮盖的简单散射作用的情况，意即在与多重散射的信号相比，简单散射信号的介质的振幅非常低的情况。这特别适合于检测埋藏在散射介质中的目标的情况。

2.技术2：通过奇异值分解的滤波

这第二项技术包括通过对旋转之后所得到的矩阵a1和a2执行奇异值分解(svd)将简单散射和多重散射相分离。svd的特性为将矩阵分解为两个子空间：“信号空间”(矩阵具有在其各行和/或各列之间存在着显著相关性的特征)以及“噪声空间”(在元素之间没有相关性的随机矩阵)。通过将svd应用于在旋转之后所得到的矩阵ar，信号空间与矩阵ar^s相对应(简单散射的作用，特征在于沿着其各列的高度相关性)，噪声空间与矩阵ar^m(多重散射的作用)有关，其中，ar＝ar^s+ar^m(在关于技术1的段落已经描述了等式6)。

矩阵ar的svd写为：

其中，u和v是尺寸为l的单一矩形矩阵。其各列ui和vi与本征向量相对应，所述本征向量与有关奇异值λi，r有关。λ是尺寸为l的矩形对角矩阵，其对角元素与按照降序排列的奇异值sλi，r相对应。在关于数据旋转的段落中，强调了矩阵ar的特殊对称性：该矩阵仅仅只包括mr个独立行，因此阶为mr<l。因此，矩阵ar仅仅只具有mr个非零奇异值，等式(15)写为：

因为简单散射的特征在于，在数据旋转之后，沿着矩阵ar各列具有很高的相干性，所以svd揭示了信号空间中的这个作用(简单散射作用与最高奇异值相关)，与此同时，多重散射的作用与最低奇异值相关。在此，与第一种滤波技术不同，在简单散射的情况下，没有关于在矩阵k(t，f)反对角上的现有相干性的形式的先验假设：只是简单地假设存在这种相干性。

问题是确定奇异值的哪一阶对应于将“信号”空间(与简单散射相关)和“噪声”空间(与多重散射相关)相分离的阈值。如果等式(5)是严格准确的，则只有第一个奇异值可能与信号空间相对应。如果假设等式(5)是不严格准确的，则简单散射的作用不是1阶的，而且多个奇异值有承载该作用的痕迹。必须构建关于分离简单散射的作用(信号空间)与多重散射的作用(噪声空间)的标准。

为此，我们利用通过随机矩阵理论所得出的结果。按照惯例和简单起见，奇异值λi，r通过其均方根作归一化：

对于大的矩阵，其中的系数是完全随机的而且其间没有相关性，第一个奇异值从不超过值(在矩形矩阵的情况下，)。

实验上，多重散射作用并非准确地与完全随机的矩阵相对应，因为传感器之间存在剩余相关(尤其是由于组件3的相邻传感器之间的机械耦合或者电耦合)，由此修改根据[由a.m.sengupta和p.p.mitra编著的《关于某些随机矩阵的奇异值分布》(详见1999年《物理评论》e版第60(3)卷，第3389-3392页)]，可以构建关于这种矩阵的奇异值的新概率论并且用其来确定的数值，由此使之能够定义关于分离信号空间与噪声空间的客观标准。

在旋转实验数据之后，待处理的矩阵ar(见等式6)因此是与简单散射相关的p<m阶矩阵ar^s以及与想要滤波的多重散射相关的m阶矩阵ar^m之和。

所提出的技术如下：在实施svd之后，中央处理器5考虑在归一化之后的第一个奇异值如果该值大于则意味着第一本征空间与简单散射相关。

然后，在2阶并且如有必要在更高阶重复该过程。

如图7所示，中央处理器5所执行的程序因此是迭代程序，包括以下子步骤：

(c31)将q初始化为1，

(c32)利用λq，r计算归一化的奇异值：

(c33)如果至少等于预定的阈值则归因于简单散射，并在q增1之后重复子步骤(c32)，

(c34)如果小于阈值则以及随后的所有奇异值都归因于多重散射。

如果的阶表示为p+1，则由此得到：

于是，矩阵ar^s包含简单散射的作用(附加剩余多重散射的作用)，矩阵ar^m与多重散射相关。

值得注意的是，技术2假设第一个归一化奇异值超出阈值它不能用于高的散射介质，意即对所述介质而言，多重散射的作用相对于简单散射而言是主要的。在这种情况下，利用将反对角投影到简单散射空间上的滤波技术来代替(技术1)，从而提取简单散射的作用。相反，如果简单散射的作用是主要的，或者与多重散射的数量级相同，则可以采用矩阵a滤波的svd技术(技术2)并由此提取多重散射的作用。

子步骤(c4)：反向数据旋转

在反向数据旋转子步骤(c4)中，中央处理器5执行子步骤(c1)中所述变换的逆向变换，并由此计算滤波窗口变换矩阵k^f(t，f)＝[k^fij(t，f)]，其中：

-在i-j是偶数的情况下：k^fij(t，f)＝a1^f(i-j)/2+m，(i+j)/2，

-在i-j是奇数的情况下：k^fij(t，f)＝a2^f(i-j-1)/2+m，(i+j-1)/2。

矩阵k^f(t，f)是尺寸为(2m-1)×(2m-1)的矩形矩阵，包含源自简单散射或多重散射的信号，根据所应用的滤波类型。图6阐释了反向数据旋转程序，图6显示了矩阵k^f(t，f)包括矩阵a1(t，f)和a2(t，f)的反对角的某些系数。

然后，可以通过各种方式利用滤波矩阵k^f(t，f)：

-如果k^f(t，f)与简单散射分量相对应，可将其具体用于检测介质1的奇点或者构建介质1的图像。为此目的，例如，可以采用两种成像方法：

按照第一种成像方法，例如，中央处理器5可以通过反傅立叶变换由各个矩阵k^f(t，f)来计算元件之间响应的滤波窗口时间矩阵h^f(t，t)，然后求不同时间矩阵h^f(t，t)之和，以便得到元件之间响应的滤波时间矩阵h^f(t)，表示在传感器组件的传感器之间的响应。然后，中央处理器通过形成基于所述元件之间响应的滤波时间矩阵h^f(t)的路径来构建介质图像。

按照第二种成像方法，称为分解时间反转算子的方法(“第二种方法(dortmethod)”，由prada等人所定义的，详见的爱思唯尔出版商的《波动》20(1994)151-163中的《时间反转算子的本征模式：多目标介质中选择性聚集的方案》)，中央处理器5可以执行以下步骤：

(d1)针对各个滤波变换矩阵k^f(t，f)，确定时间反转算子ort(t，f)＝k^f*(t，f)k^f(t，f)，它与所有或各个变换矩阵k^f(t，f)相对应，k^f*(t，f)是k^f(t，f)的复共轭矩阵，

(d2)确定所述时间反转算子的至少某些本征向量和/或本征值，

(d3)至少根据所述本征向量和/或所述本征值来检测介质中的至少一个奇点。在该步骤(d3)中，可以确定时间反转算子的本征向量vi(f)，然后在介质1的数字模型中用数字传播这些本征向量，从而确定与各个本征向量相对应的在介质1中反射物体的位置，

-如果矩阵k^f(t，f)与多重散射分量相对应，则可将其具体用于通过所述多重散射分量来计算表示介质中多重散射的重要性的指数。在这种情况下，例如，可以通过已知方式或者上述方法来构建介质的图像(超声或其它)，并且根据表示多重散射重要性的所述指数来量化所述图像的可靠性。有利的是，可以在多个点(尤其是以不同深度r)来计算该指数，并且根据表示多重散射的重要性的所述指数来量化与所述多个点相对应的图像的多个部分的可靠性。

本发明的方法改进了上述方法。

尤其是，避免在数据旋转(c2)和反向数据旋转(c4)步骤中丢失来自矩阵的信息。

实际上，如图4至图5所示，现有技术的数据旋转步骤(c2)在构建两个矩阵a1(t，f)和a2(t，f)时没有利用窗口频率变换矩阵k(t，f)的角，所以对于方法的其余计算而言，丢失了窗口频率变换矩阵k(t，f)的很大一部分数据。该窗口频率变换矩阵的四个角k1、k2、k3、k4没有用于构建矩阵a1(见图4)或者构建矩阵a2(见图5)。因此，该数据旋转步骤大体上排除了窗口频率变换矩阵的一半数据。

根据本发明方法的第一个实施例，数据旋转子步骤(c2)包括：

-第一个子步骤(c21)，在该子步骤中，将窗口频率变换矩阵k(t，f)引入(最好在中心)尺寸较大的广义矩阵ke(t，f)中，除了来自窗口频率变换矩阵k(t，f)的元素外，所述广义矩阵ke的所有元素都为零，以及，

-第二个子步骤(c22)(与现有技术的数据旋转子步骤相似)，在该子步骤中，通过从按照第一方向旋转45°的子阵的广义矩阵ke(t，f)中的提取，由广义矩阵ke(t，f)来计算两个矩阵a1(t，f)＝[a1uv(t，f)]和a2＝[a2uv(t，f)]。

调整广义矩阵ke的尺寸，以便来自窗口频率变换矩阵的元素都包含在倾斜45°的正方形ker之中，而且其本身也包含在广义矩阵ke中。尤其是，广义矩阵ke的尺寸大于或等于2xn-1。

图8显示了一个实例，在该实例中，窗口频率变换矩阵k(t，f)的尺寸为9x9(n＝9)，而且将该矩阵引入较大的广义矩阵ke的中心。于是，广义矩阵的尺寸为17x17。

广义矩阵ke因此包括角的部分kel、ke2、ke3、ke4，侧面部分ke5、ke6、、ke7、ke8以及中心部位kec。侧面部分也是正方形ker的角。除了中心部位kec以外的广义矩阵ke的所有元素(包含窗口频率变换矩阵k(t，f)的元素)都为零。换言之，角的部分kel、ke2、ke3、ke4和侧面部分ke5、ke6、ke7、ke8的所有元素都为零。

正方形ker的作用是通过采用广义矩阵ke的所有其它元素构成第二个子步骤的矩阵al和a2的基础，如下文所述。

例如，如果n是奇数，则在第一个子步骤(c21)中，广义矩阵的尺寸为2xn-1，并利用下列关系式或者任何其它等效公式，根据矩阵k(t，f)将广义矩阵ke定义为ke(t，f)＝[keij(t，f)]：

如果i∈[1+(n-1)/2；n+(n-1)/2]，以及，

j∈[1+(n-1)/2；n+(n-1)/2]

则keij(t，f)＝ki-(n-1)/2，j-(n-1)/2(t，f)，

否则keij(t，f)＝0。

如果n是偶数，则可以创建等效的公式。

于是，在第二个步骤(c22)中，通过广义矩阵ke(t，f)＝[keij(t，f)]来计算两个矩阵a1(t，f)＝[a1uv(t，f)]和a2＝[a2uv(t，f)]。

在图8所示的情况下，矩阵al的尺寸为9x9以及矩阵a2的尺寸为8x8。

实际上，矩阵al的尺寸等于窗口频率变换矩阵k(t，f)的尺寸，意即尺寸等于nxn，矩阵a2的尺寸等于窗口频率变换矩阵k(t，f)的尺寸减1，意即尺寸等于(n-1)x(n-l)。

图9显示了从图8所示的广义矩阵ke中提取的矩阵al。该矩阵al采用通过由大的点所表示的元素，使其按照第一方向(逆时针方向)旋转45°并将其放置在矩阵a1的中心部位a1c。在图8所示的广义矩阵ke用al表示的元素，在图9的矩阵a1中也用al来表示，以便显示广义矩阵ke与矩阵a1之间的元素的位移。矩阵a1的角的部分a11、a12、a13和a14的元素分别来自侧面部分ke5、ke6、ke7和ke8并且全部为零。

图10显示了从图8所示的广义矩阵ke中提取的矩阵a2。该矩阵a2采用通过由小的点所表示的元素，使其按照第一方向(逆时针方向)旋转45°并将其放置在矩阵a2的中心部位a2c。在图8所示的广义矩阵ke用a2表示的元素8，在图10的矩阵a2中也用a2来表示，以便显示广义矩阵ke与矩阵a2之间的元素的位移。矩阵a2的角的部分a21、a22、a23和a24的元素分别来自侧面部分ke5、ke6、ke7和ke8并且全部为零。

更具体而言，如果n是奇数，在第二个子步骤(c22)中，按照下列关系式或者任何其它等效公式，通过广义矩阵ke(t，f)＝[keij(t，f)]来计算矩阵a1(t，f)和a2(t，f)：

a1uv(t，f)＝keu+v-1，v-u+(n+3)/2-1+(n-1)/2(t，f)，以及，

a2uv(t，f)＝keu+v，v-u+(n+3)/2-1+(n-1)/2(t，f)。

如果n是偶数，则可以创建等效的公式。

根据本发明方法的第二个实施例，直接执行数据旋转子步骤(c2)(无需构建广义矩阵ke)。

例如，如果n是奇整数，则利用下列关系式或者任何其它等效公式，通过窗口频率变换矩阵k(t，f)＝[kij(t，f)]来计算两个矩阵a1(t，f)＝[a1uv(t，f)]和a2＝[a2uv(t，f)]：

-如果u+v-1-(n-1)/2和v-u+(n+3)/2-1都在1与n之间，包含1和n，

则a1uv(t，f)＝ku+v-1-(n-1)/2，v-u+(n+3)/2-1(t，f)，

否则a1uv(t，f)＝0，以及，

-如果u+v-(n-1)/2和v-u+(n+3)/2-1都在1与n-1之间，包含1和n-1，

则a2uv(t，f)＝ku+v-(n-1)/2，v-u+(n+3)/2-1(t，f)，

否则a2uv(t，f)＝0。

如果n是偶数，则可以创建等效的公式。

按照本发明的方法，滤波子步骤(c3)是与例如现有技术的滤波子步骤相同的。尤其是，通过矩阵a1和a2来计算两个滤波矩阵a1^f和a2^f，例如，或者利用上文所述的投影滤波技术，或者利用上文所述的奇异值分解滤波技术，或者利用任何其它技术。

滤波矩阵a1^f和a2^f所具有的尺寸与通过数据旋转步骤(c2)所确定的矩阵a1和a2的尺寸相同。

尤其是，如果n是奇数，那么有利的是，滤波矩阵a1^f的尺寸为nxn以及滤波矩阵a2^f的尺寸为(n-1)x(n-1)。

此外，在反向数据旋转子步骤(c4)中，执行针对数据旋转子步骤(c2)所述变换的大体逆向变换。在该子步骤中，通过在之前的滤波子步骤(c3)中所计算的滤波矩阵a1^f(t，f)＝[a1^fuv(t，f)]和a2^f＝[a2^fuv(t，f)]来计算滤波变换矩阵k^f(t，f)＝[k^fij(t，f)]。

该子步骤与上文所述的现有技术的反向数据旋转子步骤(c4)非常相似或者完全一致。在该子步骤中，通过按照与第一方向(按照顺时针方向旋转45°)相反的第二方向旋转，使得滤波矩阵a1^f和a2^f的中心部位的元素都包含并设置在滤波变换矩阵k^f中。滤波矩阵a1^f、a2^f的角的部分的元素未包含在滤波变换矩阵k^f中。这些元素无论如何都是零，只要这些元素都是矩阵a1和a2的角的部分的元素。

例如，如果n是偶整数，则通过下列关系式或者任何等效公式，根据两个矩阵a1^f(t，f)＝[a1^fuv(t，f)]和a2^f＝[a2^fuv(t，f)]来计算滤波变换矩阵k^f(t，f)＝[k^fij(t，f)]：

如果i-j是偶数，

则k^fij(t，f)＝a1^f(i-j)/2+(n+1)/2，(i+j)/2，

否则k^fij(t，f)＝a2^f(i-j-1)/2+(n+1)/2，(i+j-1)/2。

与现有技术的方法不同，滤波窗口频率变换矩阵k^f(t，f)的尺寸因此为nxn，该尺寸与初始窗口频率变换矩阵k(t，f)的尺寸相同。

按照现有技术的方法(见图6)，滤波窗口频率变换矩阵k^f(t，f)所具有的尺寸为(n+1)/2x(n+1)/2。其所包含的元素的数量要少得多：大约比现有技术方法的数据旋转子步骤(c2)中要丢失的元素少四倍。

通过本发明的方法，滤波窗口频率变换矩阵k^f(t，f)包含大量的元素并且有可能将大量的多重散射考虑在内。因此，可以通过波传播到更深的深度来探测介质。此外，想要生成的介质的图像具有更高的空间分辨率。有可能使用具有少量传感器的传感器组件3，因此该方法和设备的成本较低。

此外，在有利的实施例中，在确定窗口变换矩阵的子步骤(c1)中，通过窗口时间矩阵k(t，t)的小波变换来确定各个窗口频率变换矩阵k(t，f)。

时间函数f的小波变换定义如下：

使

其中：

ψ是母小波函数，

ψu，s是小波系的小波，

*表示复共轭，

u是平移因子，以及，

s是膨胀因子。

因此，小波系与滤波器组相对应。该滤波器组必须包含待研究的频率。于是，小波变换的计算等效于各个滤波器的脉冲响应与各个时间信号的卷积，脉冲响应hij(t)。窗口时间矩阵k(t，t)是在接近时间t和持续时间δt的时窗内传感器组件的传感器之间的所述脉冲响应hij(t)。窗口频率矩阵k(t，f)可以通过小波变换来计算，例如通过上述定义的卷积。

可以在下列各项中选择母小波函数ψ：

-morlet小波，例如，如图11a所示：

以及，

-maar小波(二阶高斯导数)，例如，如图11b所示：

其中以及，

-渐进小波，例如，如图11c所示：

因此，可以选择小波系，使之与传感器带宽以及待处理的脉冲信号类型(因此与介质材质)最佳地相对应。

通过利用所述小波变换，本发明的方法使之能够通过波传播更深的深度来探测介质且具有更高的精度和分辨率。

此外，根据有利的实施例，在发射步骤(a)中，传感器组件3发射入射波，所述入射波按照预定角度α倾斜于所述介质1的外表面1a，如图12所示。

为此，将传感器的组件3置位于所示的耦合介质7之中。该耦合介质7可置位于组件3与待探测的介质的外表面1之间，或者使该耦合介质7与探针集成为一体，所述探针至少包含组件和所述耦合介质。

例如，耦合介质7所具有的折射指数n7不同于待探测的介质1的折射指数n1。因此，在该介质中的传播速度分别为v1和v7。

于是，按照滤波子步骤(c3)的投影滤波技术，通过下列修改的公式来确定列向量s＝[su]的分量：

其中：

df是焦距，它是通过两个介质之间的指数变化进行校准的在耦合介质7中行进的第一距离d7与在介质中行进的第二距离d1之和；换言之：

由于采用倾斜入射波的发射，本发明的方法还得以改进并且使之能够通过更大深度的波传播来探测介质且具有更高的精度和分辨率。尤其是，可以得到更多关于探测介质1中任何缺陷的几何图形(平面或立体)的信息。