一种有源周期信号中有效信息提取的方法及装置与流程

本发明涉及周期信号处理领域，更具体地，涉及一种有源周期信号中有效信息提取的方法及装置。

背景技术：

目前，周期信号的应用非常广泛，包括震动周期信号、电磁周期信号及机械周期信号等等。绝大多数情况下，周期信号是由一个主频信号和许多谐波信号组成的，在实际应用中不同的构成特征反映了不同的物理意义，通过挖掘这些信号中不同频率的特征，可以解决许多实际应用问题。但是在实际应用中，信号总是受到各种各样的噪声影响，当干扰复杂时，提取有效信号即高信噪比的信号会变得非常困难。

随着人类活动区域的进一步扩大，工业的持续发展，当今所采集的电磁勘探信号中总存在着各种各样的电磁干扰，严重影响了信号的信噪比，对电磁勘探的效果带来了消极的影响。在噪声很大时，往往只提取信号的主频部分，或者通过经验提取能量较大的谐波成分，有时根据经验提取的信号是不符合质量要求的信号，没有一种标准来指导有效数据的提取。因此急需一种针对周期信号的噪声评价及有效信息提取的方法来指导工作和生产。

技术实现要素：

本发明提供一种克服上述问题或者至少部分地解决上述问题的。

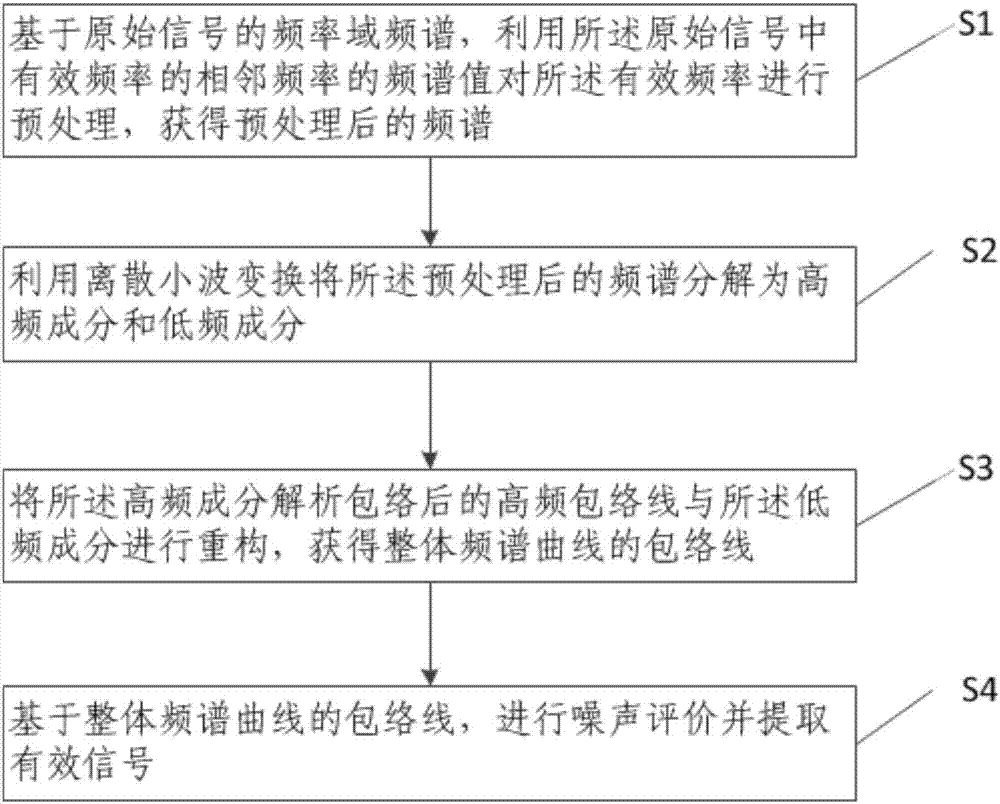
根据本发明的一个方面，提供一种有源周期信号中有效信息提取的方法，其特征在于，包括：

S1，基于原始信号的频率域频谱，利用所述原始信号中有效频率的相邻频率的频谱值对所述有效频率进行预处理，获得预处理后的频谱；

S2，利用离散小波变换将所述预处理后的频谱分解为高频成分和低频成分；

S3，将所述高频成分解析包络后的高频包络线与所述低频成分进行重构，获得整体频谱曲线的包络线；

S4，基于整体频谱曲线的包络线，进行噪声评价并提取有效信号。

进一步，所述S1进一步包括：

S1.1，利用混合基快速傅里叶变换获得所述原始信号的频率域频谱；

S1.2，将所述原始信号中有效频率的频谱值设置为相邻频率的频谱值的平均值，从而获得预处理后的频谱。

进一步，所述S2进一步包括：

S2.1，对所述预处理后的频谱进行第一级离散小波变换，分解为第一低频部分和第一高频部分；

S2.2，对所述第一低频部分进行第二级离散小波变换，分解为第二低频部分和第二高频部分；

S2.3，对所述第二低频部分进行第三级离散小波变换，分解为第三低频部分和第三高频部分。

具体的，所述S1中所述高频成分为所述第一高频部分、所述第二高频部分和所述第三高频部分叠加后的高频成分；所述低频成分为所述第三低频部分。

进一步，所述S3进一步包括：

S3.1，利用希尔伯特变换对所述高频成分进行解析包络，获得第一包络线；

S3.2，选取所述第一包络线的极大值进行样条插值，获得所述高频包络线；

S3.2，将所述高频包络线与所述低频成分进行重构，获得整体频谱曲线的包络线。

进一步，所述S4进一步包括：

S4.1，将所述整体频谱曲线的包络线在有效频率的频谱值除以所述有效频率的原始频谱值，得到噪声评价系数；

S4.2，基于所述噪声评价系数，提取所有噪声评价系数小于要求数值的有效频率为所述有效信号。

具体的，S3.1中所述希尔伯特变换为：

f_A(s)＝f(s)+iH(f(s))

其中，f(s)为原始信号，H(f(s))为对f(s)进行希尔伯特变换得到的信号且f_A(s)为希尔伯特解析信号，|f_A|即为对应实数信号的上包络曲线。

进一步，所述S4.1进一步包括：

S4.1.1，获取所述整体频谱曲线的包络线在所有有效频率的频谱值，以及获取所有有效频率的原始频谱值；

S4.1.1，基于每一个有效频率，将所述整体频谱曲线的包络线在有效频率的频谱值除以所述有效频率的原始频谱值，得到每一个有效频率的噪声评价系数。

具体的，所述有效频率包括主频和谐波。

根据本发明的另一个方面，还提供一种有源周期信号中有效信息提取的装置，包括：

预处理模块，用于基于原始信号的频率域频谱，利用所述原始信号中有效频率的相邻频率的频谱值对所述有效频率进行预处理，获得预处理后的频谱；

高低频分解模块，用于利用离散小波变换将所述预处理后的频谱分解为高频成分和低频成分；

包络线模块，用于将所述高频成分解析包络后的高频包络线与所述低频成分进行重构，获得整体频谱曲线的包络线；

有效信号提取模块，用于基于整体频谱曲线的包络线，进行噪声评价并提取有效信号。

本申请提出一种有源周期信号中有效信息提取的方法及装置，通过对原始信号的频谱进行预处理后，分解为高频成分和低频成分，对其中的高频成分进行二次包络处理后再与低频成分进行重构获取整体信号包络线，基于整体信号包络线而提出后一种噪声评价方法；利用所述噪声评价方法，不需要进行准确计算，只需要通过估计振荡函数的上界来估计噪声的最大影响。应用所述噪声评价方法，能够得到不同频率信号的信噪比数值，并以此提取符合生产要求的有效信号信息。本申请所述噪声评价及提取有效信息方法可以应用于所有周期信号，尤其是对周期信号中不容易分解的非周期噪声的影响评价具有良好的效果，可以大大的提高有效信号提取的数量和效率，具有良好的应用前景。

附图说明

图1为本发明一种有源周期信号中有效信息提取的方法流程图；

图2为本发明所述原始信号频率域频谱曲线示意图；

图3为本发明对所述原始信号频率域频谱预处理后的频谱示意图；

图4为本发明对所述预处理后的频谱信号进行三级小波分解的示意图；

图5为本发明应用三级小波分解后的高频部分和低频部分示意图；

图6为本发明基于希尔伯特变换的解析包络理论示意图；

图7为本发明第一实施例高频部分的包络结果示意图；

图8为本发明第一实施例整体包络结果示意图；

图9为本发明第一实施例包络计算后包络比例统计结果示意图；

图10为本发明第一实施例噪声最大影响和实测数据的关系示意图；

图11为本发明第一实施例通过包络后噪声的估计评价数示意图；

图12为本发明第一实施例实际数据的包络结果示意图；

图13为本发明第一实施例实际数据按5％误差提取有效频点结果示意图；

图14为本发明第一实施例实际数据按3％误差提取有效频点结果示意图。

具体实施方式

下面结合附图和实施例，对本发明的具体实施方式作进一步详细描述。以下实施例用于说明本发明，但不用来限制本发明的范围。

本发明以周期电磁勘探信号为例来说明所述一种有源周期信号中有效信息提取的方法。有源电磁勘探信号一种非常重要的周期信号，在地球物理勘探领域有非常重要的作用。电磁勘探方法是一种基于麦克斯韦电磁传播理论的重要地球物理勘探方法。无论是针对大地构造、油气勘探、矿藏勘察，还是针对各种工程勘探，都起到重要的作用，解决了大量的实际问题。

如图1所示，一种有源周期信号中有效信息提取的方法，包括：

S1，基于原始信号的频率域频谱，利用所述原始信号中有效频率的相邻频率的频谱值对所述有效频率进行预处理，获得预处理后的频谱；

S2，利用离散小波变换将所述预处理后的频谱分解为高频成分和低频成分；

S3，将所述高频成分解析包络后的高频包络线与所述低频成分进行重构，获得整体频谱曲线的包络线；

S4，基于整体频谱曲线的包络线，进行噪声评价并提取有效信号。

本发明创新在于通过在周期信号的频率域上的噪声评价来估计噪声的影响上界，而不是传统上估计噪声的频谱值。本发明中噪声分为周期噪声和非周期噪声两大类，周期噪声的影响容易分开，本发明着重针对非周期噪声的影响进行估计。由于非周期噪声的频谱是复杂的高振荡曲线，没有数学算法可以只在频率域解出其准确值；本发明并不需要计算出噪声的准确值，只需要通过估计振荡函数的上界来估计噪声的最大影响。如果噪声的最大影响依然符合信号规范的要求，那么噪声的实际影响值一定符合规范的要求。

作为一个可选的实施例，所述S1进一步包括：

S1.1，利用混合基快速傅里叶变换获得所述原始信号的频率域频谱；

S1.2，将所述原始信号中有效频率的频谱值设置为相邻频率的频谱值的平均值，从而获得预处理后的频谱。

图2为本发明对原始信号数据的频谱曲线。在本实施例中所述原始信号为仿真信号，所述仿真信号拥有1Hz的主频，并存在3～199Hz共计99个谐波成分，能量最大值为60，能量依次衰减。如果没有噪声干扰时，有效信号的频率谱为一系列的尖脉冲，但是实际数据总是受到各种干扰影响，在频率域能量不再只分布在那些有效频点上，在所有频率位置都存在能量。

本发明通过估计振荡函数计算噪声部分在有效频率的影响最大值；在进行估计之前，需要优化原始频谱图。本实施例的优化处理是：将原始信号频谱的有效频率的频谱值设置为相邻两个频率的谱数值的平均数，其他频率位置的频谱值保持不变，从而获得噪声的预处理频谱图，为接下来的估计算法准备。图3示为对所述原始信号频率域频谱预处理后的频谱示意图。如图3所示，与图2相比，在有效频率点位置的脉冲消失了。

作为一个可选的实施例，所述S2进一步包括：

S2.1，对所述预处理后的频谱进行第一级离散小波变换，分解为第一低频部分和第一高频部分；

S2.2，对所述第一低频部分进行第二级离散小波变换，分解为第二低频部分和第二高频部分；

S2.3，对所述第二低频部分进行第三级离散小波变换，分解为第三低频部分和第三高频部分。

作为一个可选的实施例，所述S1中所述高频成分为所述第一高频部分、所述第二高频部分和所述第三高频部分叠加后的高频成分；所述低频成分为所述第三低频部分。

图4为本发明对信号对所述原始信号进行三级小波分解的示意图。本实施例中，首先对信号S进行第一级小波分解得到第一低频部分A1和第一高频部分D1；然后对第一低频部分A1进行第二级小波分解，得到第二低频部分A2和第二高频部分D2；再对第二低频部分A2进行第三级小波分解得到第三低频部分A3和第三高频部分D3。

图5为本发明中应用三级小波分解的高频部分和低频部分。如图5所示频域信号被分成低频成分和高频成分。其中低频成分为A3，而高频成分为D1+D2+D3。

作为一个可选的实施例，所述S3进一步包括：

S3.1，利用希尔伯特变换对所述高频成分进行解析包络，获得第一包络线；

S3.2，选取所述第一包络线的极大值进行样条插值，获得所述高频包络线；

S3.2，将所述高频包络线与所述低频成分进行重构，获得整体频谱曲线的包络线。

图6为本发明中基于希尔伯特变换的解析包络理论示意图。本实施例中原始信号为一段窄带振荡信号f(s)，是一段衰减函数和一段振荡函数的乘积信号。对f(s)进行希尔伯特变换得到H(f(s))，把H(f(s))作为虚部，f(s)作为实部，构成一个新的信号f_A(s)，称作为基于希尔伯特的解析信号，见式(1)

f_A(s)＝f(s)+iH(f(s)).(1)

f_A即为构成的解析信号，|f_A|即为对应实数信号的上包络曲线，其中

图6中振荡曲线的上方的连续曲线即为包络曲线，可以发现原始振荡曲线在所有位置都小于包络曲线的数值。需要注意的是，基于希尔伯特变换的解析包络方法是针对窄带振荡曲线的，所以原始频谱并不符合这样的条件，不应该直接对原始频率谱进行包络，但是对原始小波进行小波分解后，高频部分可以认为在局部上是符合基于希尔伯特变换的解析包络要求的。为了获得更好的包络结果，本发明在希尔伯特包络的基础上再进行了一次极值包络，即选取第一次包络曲线的极大值，然后进行样条插值获取第二次包络曲线。

如图7所示，应用基于希尔伯特变换的解析包络方法和极值包络法对图5中频率谱的高频成分进行包络，振荡曲线上方连续的曲线即为包络线，为本发明所述高频包络线。

图8为本发明中对图2中的仿真信号进行整体包络结果。根据图7中得到的高频曲线振荡部分的包络曲线，与图5中的低频部分重构得到原始频谱的包络曲线。

作为一个可选的实施例，所述S4进一步包括：

S4.1，将所述整体频谱曲线的包络线在有效频率的频谱值除以所述有效频率的原始频谱值，得到噪声评价系数；

S4.2，基于所述噪声评价系数，提取所有噪声评价系数小于要求数值的有效频率为所述有效信号。

本实施例中，提取整体频谱曲线的包络线在有效频率点的对应的数值，通过估计算法可以估计得到的噪声在有效频率位置的最大影响值。

作为一个可选的实施例，所述S4.1进一步包括：

S4.1.1，获取所述整体频谱曲线的包络线在所有有效频率的频谱值，以及获取所有有效频率的原始频谱值；

S4.1.2，基于每一个有效频率，将所述整体频谱曲线的包络线在有效频率的频谱值除以所述有效频率的原始频谱值，得到每一个有效频率的噪声评价系数。

具体的，所述有效频率包括主频和谐波。

图9示为本发明第一实施例包络计算后包络比例统计结果示意图。由于采用的是仿真信号，所以噪声的实际频谱是已知的，所以可以对包络后的估计值与真实值进行比较，来判断包络比例。

如图9a所示，为针对仿真信号包络比例进行了统计，其中100个频率点中90个频率点位置的包络值要大于噪声的实际能量值。如图9b所示，10个包络值小于噪声能量值的位置，基本上也大于噪声能量值的70％，说明包络值和噪声在有效频率能量值是在同一尺度，同样能够反映噪声的影响幅度。综上，包络曲线在有效频率的数值能够作为衡量噪声最大影响幅度的标准。

图10为本发明第一实施例噪声最大影响和实测数据的关系示意图。如图10所示的噪声在有效频点的最大影响值与实测数据的关系图，在有效频率的准确值将会落在虚线框内，而准确值就是需要获取的有效信号；最大影响值越小，则虚线框的半径就越小，所获取的有效信号就越可靠。

图11为本发明通过包络后噪声的估计评价数示意图。如图11所示为仿真信号噪声最大影响值与实测数据频谱相比得到的噪声评价数曲线。如果认为小于5％认为是合格的信号，将有93个频点符合要求，这相比只根据经验提取几个有效频率信号是非常高效的，所以通过本发明中提到的噪声评价方法可以更有效的提取合格的有效信号。

图12为本发明第一实施例实际数据的包络结果示意图。如图12所示，针对2ⁿ序列伪随机电磁勘探的实际采集数据应用本发明中的包络算法计算噪声的影响，下部锯齿状连续曲线为噪声的频谱，上部的连续曲线为其包络曲线，而尖脉冲位置为有效信号位置。

图13为本发明第一实施例实际数据按5％误差提取有效频点结果示意图。根据图12中得到的包络曲线结果，计算所有有效频点(包括主频和谐波)位置的噪声评价数，提取所有噪声评价数小于5％的结果。其中可以发现过去只提取主频信号，40Hz以下信号共计28个频率，而通过应用本发明能够提取到105个频率，大大提高了有效信号的数量和效率。

图14为本发明第一实施例实际数据按3％误差提取有效频点结果示意图。根据图12中得到的包络曲线结果，计算所有有效频点(包括主频和谐波)位置的噪声评价数，提取所有噪声评价数小于3％的结果。只提取主频信号，40Hz以下信号共计28个频率，而通过应用本发明能够提取到44个频率，大大提高了有效信号的数量和效率。

本发明还提供一种有源周期信号中有效信息提取的装置，包括：

预处理模块，用于基于原始信号的频率域频谱，利用所述原始信号中有效频率的相邻频率的频谱值对所述有效频率进行预处理，获得预处理后的频谱；

高低频分解模块，用于利用离散小波变换将所述预处理后的频谱分解为高频成分和低频成分；

包络线模块，用于将所述高频成分解析包络后的高频包络线与所述低频成分进行重构，获得整体频谱曲线的包络线；

有效信号提取模块，用于基于整体频谱曲线的包络线，进行噪声评价并提取有效信号。

总体而言，本发明涉及一种基于混合基快速傅里叶变换(Mix Radix FFT)、离散小波变换(DWT)及希尔伯特变换(Hilbert Transform)的针对周期信号的噪声评价方法，并根据受噪声影响情况提取符合条件的高信噪比信号。所述方法包括：应用混合基快速傅里叶变换获得原始信号的频率域频谱；在频率域，将有效频率的频谱值设为相邻频率的频谱值的平均值，作为预处理后的频谱；应用离散小波变换将预处理频谱曲线分成高频成分(H)和低频成分(L)；对分解得到的高频成分进行基于希尔伯特变换的解析包络，同时为了获得更大的包络比例，可以对包络曲线再做一次极值包络，然后得到的包络曲线与小波分解的低频成分重构得到整体频谱曲线的包络线；拾取包络线在有效频率的数值，除以在有效频率位置的原始频谱值，得到噪声影响程度值，即噪声评价系数；根据噪声影响程度值，提取符合信噪比要求的有效信号。

本发明所述噪声评价及有效信号提取的方法，能够得到不同频率信号的信噪比数值，并以此提取符合生产要求的有效信号信息；所述噪声评价及提取有效信息方法可以应用于所有周期信号，尤其是对周期信号中不容易分解的非周期噪声的影响评价具有良好的效果，可以大大的提高有效信号提取的数量和效率，具有良好的应用前景。

最后，本申请的方法仅为较佳的实施方案，并非用于限定本发明的保护范围。凡在本发明的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。