基于Ｓtacked　ＳＡＥ深度神经网络的轴承故障诊断方法与流程

本发明属于信号的智能分析检测领域，具体涉及基于堆叠稀疏自动编码器(Stacked SAE)深度神经网络的轴承故障定性、定量、层次化诊断方法研究。

背景技术：

随着经济的发展，人们对设备故障诊断技术的要求越来越高，不仅仅需要判断故障类型，还需要进一步判断故障的严重程度，并且要求其适用于大数据的处理。轴承作为旋转机械的关键零部件之一，其状态直接影响到旋转机械的运行状态，一旦轴承出现故障，将很可能带来巨大的经济损失，甚至导致人员伤亡。信号处理与分析是实现轴承故障诊断的有效途径之一，常用的方法主要有时域统计量分析、包络分析、时频分析、经验模态分解及其改进算法、小波分析、以及谱峭度分析等。虽然这些方法已广泛应用于轴承的故障诊断，但是往往要求检测人员具有极其丰富的信号处理与分析的专业知识，需要依靠专业人员进行轴承故障特征的提取并识别故障，对于大数据的分析与处理存在很大的局限性。为了实现故障的智能诊断，减少人力的消耗，人工神经网络被广泛研究并运用于轴承的故障诊断，虽然后期省去了人工识别故障，节省了部分人力，但是要想取得较高的故障识别精度仍然依赖于前期人为提取极为鲜明的特征，仍然对专业的信号处理与分析方法具有极大的依赖性。此外，轴承的故障诊断不仅仅涉及故障类型的诊断，还涉及到故障严重程度的诊断，前者可以提供轴承的健康状态，保证生产运行的安全，同时在发生故障时给维修人员提供所需维修的部位，减少故障排查的时间；后者可以给维修人员提供所需维修部件的轻重缓急，在多个部件发生故障时，决定维修的先后顺序，两者对生产安全均具有重大的意义。然而目前研究较多的故障诊断方法，不论是基于信号处理与分析，或者是人工神经网络方法，均局限于解决判断轴承的故障类型，既能判断故障类型又能判断故障大小的方法少有研究，因而目前急需一种轴承故障定性、定量、层次化的诊断方法，既能定性判断轴承的故障类型，又能定量判断故障的严重程度，同时还能达到不过多依赖于专业人员进行故障特征的提取以及故障的识别，使其更加适用于大数据时代。

鉴于上述的缺陷，本设计人，积极加以研究创新，以期创设一种基于堆叠稀疏自动编码器(Stacked SAE)深度神经网络的轴承故障定性、定量、层次化诊断方法，使其更具有产业上的利用价值。

技术实现要素：

为解决上述技术问题，本发明的目的是提供一种基于堆叠稀疏自动编码器(Stacked SAE)深度神经网络的轴承故障定性、定量、层次化诊断方法，既能通过第一层的深度神经网络实现轴承故障类型的定性化判断，又能通过第二层的深度神经网络实现轴承故障大小的定量化判断。此外，该发明利用EMD分解提取AR模型参数作为原始轴承信号的预处理，大大降低输入信号的维度，减小计算量。同时，该发明所基于的深度神经网络，能够利用自身的非线性变换实现特征的自动提取并自动分类，降低对信号处理专业知识的依赖并减少人力的消耗。

本发明提出的基于Stacked SAE深度神经网络的轴承故障诊断方法，包括如下步骤：

步骤1：结合EMD分解和AR模型，对采集到的原始轴承振动信号提取AR模型参数作为网络的输入，实现信号降维预处理，大大减少计算量，提高网络的训练及测试速度。

步骤2：根据堆叠稀疏自动编码器，以下简称Stacked SAE，构建两层的层次化故障诊断深度神经网络，第一层用于判断故障类型，即故障的定性判断，第二层用于判断故障大小，即故障的定量判断。输入训练样本集，通过反向传播优化算法，得到每一层的Stacked SAE的网络参数，从而得到该发明所提出的定性、定量、层次化的深度神经网络诊断模型。

步骤3：将测试样本集输入到已训练好的定性、定量、层次化的深度神经网络诊断模型，通过实际的输出标签值来定性、定量化判断该测试样本所属的故障类型以及故障大小。

进一步的，所述步骤1包括：

步骤1.1：对采集到的原始非平稳的轴承振动信号s(t)进行EMD分解，将其分解为有限个平稳的IMF分量，可表示为：

其中，c_a(t),a＝1,2L m代表原始信号经过EMD分解得到的m个平稳的IMF分量，这m个IMF分量分别包含从高频到低频的频率成分。r_m代表分解后的残余项。

步骤1.2：若采集到的故障信号包含B种类型，任选每种类型中的一个信号，设其各自经过EMD分解得到的第一个IMF分量的离散值用序列表示为c_1z(t)，z＝1,2,L B，且长度均为N。对每个c_1z(t)建立AR模型可表示为：

其中，p_z(z＝1,2,L B)代表各个AR模型的阶数，a_zk(k＝1,2L p_z)代表各个模型的p_z个自回归系数，w_z(t)代表各个模型的拟合残差，是均值为0，方差为的白噪声序列。

步骤1.3：利用最终预测误差准则，即FPE准则，来确定AR模型的最佳阶数，当准则取最小值时的阶数p_z为各个AR模型的最佳阶数。FPE准则可表示为：

为计算方便，取p_z(z＝1,2,L B)中的最小值作为所有IMF分量建立AR模型的标准模型阶数，并记为P。

步骤1.4：确定各个AR模型的标准模型阶数P之后，每个AR模型的系统函数均可表示为：

Y＝XA+W (4)

其中：

Y＝[c_P+1 c_P+2 L c_N]^T (5)

A＝[a₁ a₂ L a_P]^T (6)

W＝[w_P+1 w_P+2 L w_N]^T (7)

然后利用最小二乘法求解AR模型的自回归系数A，表示为：

A＝(X^TX)^-1X^TY (9)

方差可用自回归系数表示为：

由于轴承的故障信息主要集中于高频段，因而本发明只考虑原始信号经过EMD分解得到的前4个IMF分量。那么对前4个IMF分量而言，每一个IMF分量所得到的AR模型参数，包括自回归系数以及方差可表示为一个P+1维的向量ARP_e：

对任意一个原始轴承振动信号，可将其前4个IMF分量的AR模型参数转换成特征向量x作为模型的输入，表示为：

步骤1通过EMD分解和AR模型相结合，提取出能反应轴承状态信息的AR模型参数作为网络的输入，不但能提高模型的诊断精度，而且能将原始轴承信号降维，简化模型训练以及测试过程中的计算量，加快了网络的训练以及测试速度。

进一步的，所述步骤2包括：

步骤2.1：若每种故障类型的信号包含D种故障大小，每种故障大小有E个信号样本，那么一共有B*D*E个信号样本，则需要重复步骤1.4B*D*E次，求出每一个轴承信号的4*(P+1)维特征向量作为模型的输入，并将每种轴承状态下样本总数的2/3作为训练样本，另外1/3作为测试样本。

步骤2.2：利用一个Stacked SAE搭建该发明的第一层网络，用于定性化诊断轴承的故障类型。由步骤2.1可知，用于第一层轴承故障定性化诊断的训练样本数为B*D*E*2/3,可简记为G。在初步确定Stacked SAE的隐藏层数U，每个隐藏层的单元数以及学习率的情况下，将步骤1.4中得到的训练样本集的特征向量作为输入，那么可通过预训练和微调来确定定性诊断网络每一层最终的最佳权重矩阵以及偏置项。

(1)预训练的步骤为：

a)对一个含有U个隐藏层的Stacked SAE，每一个隐藏层均与上一层构成一个SAE的编码网络。因而，可将输入层和第一个隐藏层视为第一个SAE的编码网络，然后通过反向传播优化算法求得SAE代价函数取得最小值时的权重矩阵和偏置项。假设x^d为训练样本集中的任意一个训练样本，暂不考虑稀疏项，那么自动编码器的代价函数可表示为：

其中，表示该样本x^d经过自动编码器所得到的输出，即自动编码器的重构信号。用L2范数来表示数据保真项。第二项是正则化项，用于抑制权重的幅值，防止过拟合，λ是权重衰减系数，n_l是自动编码器的层数，即为3，S_l是第l层的神经元个数。W＝{W⁽¹⁾,W⁽²⁾}代表自动编码器编码网络与解码网络的权重矩阵，b＝{b⁽¹⁾,b⁽²⁾}代表自动编码器编码网络与解码网络的偏置项，代表第l层的j单元与第l+1层的i单元之间的连接权值。

若对自动编码器加上稀疏惩罚项，则相应的稀疏自动编码器SAE的代价函数可表示为：

其中第一项如式(13)所示，第二项是稀疏惩罚项，β代表稀疏惩罚系数，ρ是一个接近于0的极小值，代表第g个神经元的平均激活值，S₂代表SAE隐藏层的单元数。

利用反向传播算法，通过不断减小代价函数式(14)，当达到指定的迭代次数或者代价函数下降到指定值时，可得到第一个SAE编码网络和解码网络的最佳权重矩阵以及偏置项那么，对输入样本x^d而言，第一个隐藏层的输出向量h₁^d可表示为：

其中f是激活函数，本发明采用S型函数，即

b)第一个隐藏层和第二个隐藏层可视为第二个SAE的编码网络，并将第一个隐藏层的输出作为第二个SAE的输入。同样运用反向传播算法，通过不断减小第二个SAE的代价函数，从而得到编码网络和解码网络的最佳权重矩阵以及偏置项那么，第二个隐藏层的输出向量h₂^d可表示为：

c)以此类推，包含U个隐藏层的Stacked SAE需要重复预训练U次，直到第U个SAE预训练完成，并得到编码网络和解码网络的最佳权重矩阵以及偏置项那么第U个隐藏层的输出h_U^d可表示为：

h_U^d＝f(W_U⁽¹⁾h_U-1^d+b_U⁽¹⁾) (18)

d)网络的输出层可视为一个分类器，输出向量的每一个元素分别对应该样本属于每种类别的概率值。由步骤1已知，信号样本一共包含B种故障类型，因而标签可记为1,2，L，B。本发明采用softmax分类器，输入即为第U个隐藏层的输出h_U^d。设输入样本x^d的理想标签是y^d，那么实际的输出向量O^d可表示为:

其中θ表示softmax分类器的权重矩阵，可表示为：

softmax分类器的代价函数可以表示为：

其中，第二项是权重衰减项，用来抑制过拟合。与SAE的预训练类似，softmax分类器的预训练同样是利用反向传播算法求代价函数最小值时的最佳权重矩阵θ。

(2)微调的步骤为：

将预训练步骤得到的U个SAE编码网络的最佳权重矩阵L，偏置项L,以及softmax分类器的最佳权重矩阵θ作为定性诊断网络每一层的初始权重矩阵和偏置项，利用反向传播算法再次迭代和更新各个权重矩阵和偏置项，直到达到最大的迭代次数或者softmax分类器的代价函数值下降到指定值，从而获得定性诊断网络每一层最终的最佳权重矩阵L，θ_f以及偏置项L，至此，用于轴承故障定性诊断的第一层深度神经网络训练完毕。

步骤2.3：同样利用Stacked SAE搭建第二层的故障诊断深度神经网络，用于定量诊断轴承的故障大小。由于样本信号一共包含B种故障类型，每种故障类型包含D种故障大小，则第二层的定量化诊断网络共需要B个Stacked SAE来实现各种故障类型下故障大小的分类，每一个Stacked SAE对应一种故障类型，用于定量区分D种故障大小，各种故障大小的标签分别记为1,2,L,D。

对每一个Stacked SAE重复执行步骤2.2，在初步确定每个Stacked SAE的隐藏层数U，每个隐藏层的单元数以及学习率的情况下，将属于同一种故障类型但是故障大小不同的训练样本集作为输入，那么对于每个Stacked SAE均有D*E*2/3的训练样本，通过预训练和微调来确定每个Stacked SAE每一层最终的最佳权重矩阵L，偏置项L，以及softmax分类器最终的最佳权重矩阵θ_f。至此，用于轴承故障定量分类的第二层深度神经网络训练完毕。

最终，我们可以得到一种基于堆叠稀疏自动编码器(Stacked SAE)深度神经网络的轴承故障定性、定量、层次化诊断方法。网络的第一层用一个Stacked SAE实现B种故障类型的轴承故障定性化分类，第二层用B个Stacked SAE分别实现B种故障类型下D种不同故障严重程度的轴承故障定量化分类。步骤1中所提出的将原始轴承信号经过EMD分解之后提取的AR模型参数作为网络的输入，大大降低网络的输入维度，有利于减小网络训练及测试过程中的计算量，保证该网络的训练以及测试速度。此外，该发明所基于的深度神经网络能进一步自动对输入提取特征并实现自动化诊断，在保证较高的诊断精度的同时，降低了对信号处理专业知识的依赖性，并且减少了人力的消耗，在大数据时代下更加具有实用价值。

进一步的，所述步骤3包括：

步骤3.1：将经过步骤1得到的测试样本集输入到步骤2中已训练好的定性、定量、层次化的轴承故障诊断深度神经网络，先利用第一层的Stacked SAE进行轴承故障定性分类，根据实际输出的标签值来判断该轴承是否存在故障以及故障类型。

步骤3.2：根据第一层的轴承故障定性诊断结果，将测试样本送到相应的第二层的Stacked SAE中进行轴承故障定量诊断，再次根据实际的输出标签值来定量化判断该轴承的故障严重程度。

因而，通过该发明所提出的基于Stacked SAE的轴承故障定性、定量、层次化的深度神经网络诊断方法，对采集到的任意轴承振动信号，可首先通过EMD分解提取AR模型参数实现原始信号的降维，大大减小计算量。然后通过基于Stacked SAE的层次化诊断深度神经网络，分别在网络的第一层、第二层实现轴承故障的定性、定量诊断，从而解决了生产维修中的两大难题：所需维修的部位在哪，以及维修的轻重缓急该如何决定。此外，即使在大数据时代下，面临着大量采集的信号样本，该发明所能达到的自动提取特征以及自动识别故障类型跟故障的严重程度大大减少了人力物力的消耗，更加具有实用价值。

借由上述方案，本发明至少具有以下优点：

1、该发明所提出的层次化故障诊断网络不仅仅可以定性化判断轴承故障类型，而且还可以定量化判断轴承的故障严重程度，前者可以给维修人员准确地提供所需维修的部位，减少排查时间，后者可以在多故障情况下，给维修人员提供所需维修部位的轻重缓急；

2、该发明所提出的将EMD分解之后提取AR模型的参数作为网络的输入，大大降低输入维度，有利于减小网络训练以及测试过程中的计算量；

3、该发明所基于的深度神经网络，无需过多依赖于人工提取非常鲜明的特征，能利用自身的非线性变换自动对输入提取特征，精度比传统的故障诊断方法均高，且能实现故障的智能诊断，更加的省时省力；

4、基于本发明，在大数据时代下，面对大量采集到的轴承信号，人们可根据本发明第一层的定性化诊断结果直接获得轴承的运行状态以及发生故障时所需维修的部位，然后根据第二层的定量化判断结果来决定部件维修的轻重缓急，无需人工诊断，省时省力。

上述说明仅是本发明技术方案的概述，为了能够更清楚了解本发明的技术手段，并可依照说明书的内容予以实施，以下以本发明的较佳实施例并配合附图详细说明如后。

附图说明

图1为自动编码器的示意图；

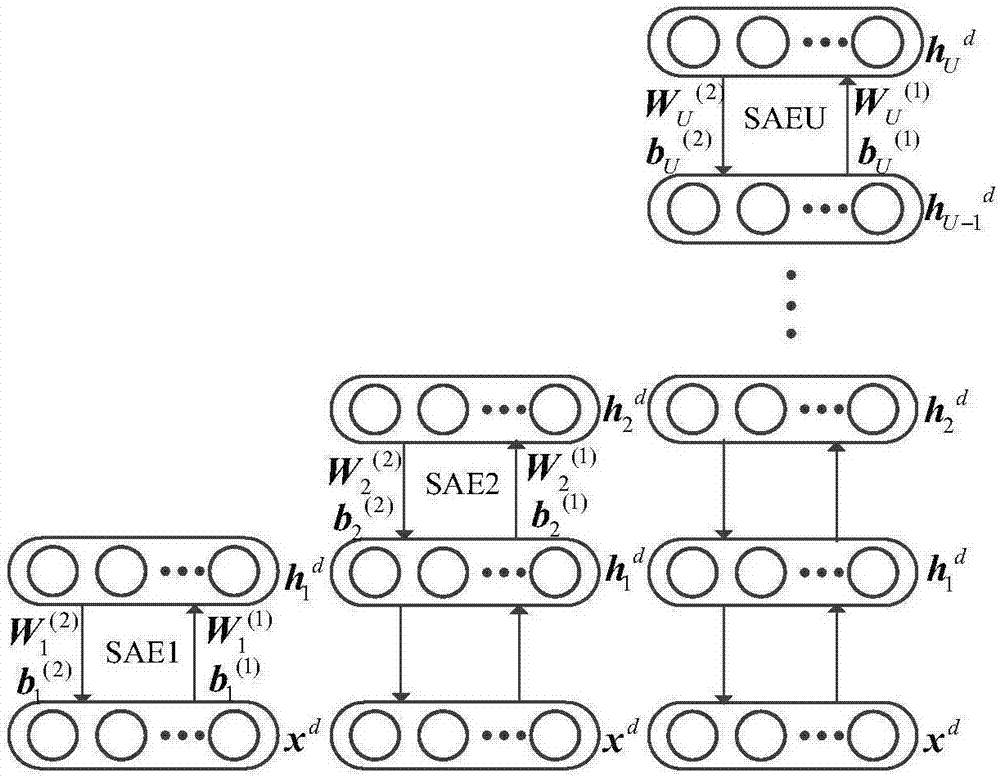
图2为堆叠稀疏自动编码器(Stacked SAE)的示意图；

图3为本发明所用实验数据的时域波形图；

图4为本发明提出的基于堆叠稀疏自动编码器(Stacked SAE)深度神经网络的轴承故障定性、定量、层次化诊断方法流程图；

图5为本发明提出的基于堆叠稀疏自动编码器(Stacked SAE)深度神经网络的轴承故障定性、定量、层次化诊断方法示意图；

图6为本发明对实验数据的故障定性识别结果示意图；

图7为本发明对实验数据的故障定量识别结果示意图。

具体实施方式

下面结合附图和实施例，对本发明的具体实施方式作进一步详细描述。以下实施例用于说明本发明，但不用来限制本发明的范围。

下面结合实际的实验数据对本发明进行详细说明：

实验数据采用凯斯西储大学的轴承数据集，一共包含4种故障类型：内圈故障、滚动体故障、外圈故障以及正常状态，分别定义各自的理想标签为1，2，3，4，时域波形图如图3所示。每种故障状态下的故障大小包含3种尺寸：0.007英寸、0.014英寸和0.021英寸，分别定义各自的标签为1，2，3，因而一共有3*3+1＝10种运行状态。采样频率为12KHz，每种运行状态下采样600个信号样本，每个信号的长度N为1000点，因而一共有6000个信号样本，其中内圈故障、滚动体故障以及外圈故障各自包含1800个样本，正常状态下包含600个样本。

如图4所示，本发明包括以下步骤：

步骤1：结合EMD分解和AR模型，对采集到的原始轴承振动信号提取AR模型参数作为网络的输入，实现信号的降维预处理，有利于简化网络训练以及测试过程中的计算；

步骤2：根据堆叠稀疏自动编码器，以下简称Stacked SAE(传统的自动编码器如图1所示，本发明的堆叠稀疏自动编码器如图2所示)，构建两层的层次化故障诊断深度神经网络，第一层网络用于定性化判断轴承的故障类型，第二层网络用于定量化判断轴承的故障严重程度，输入训练样本集，通过反向传播优化算法，得到每一层的Stacked SAE的网络参数，从而得到该发明所提出的定性、定量、层次化的深度神经网络诊断模型；

步骤3：将测试样本集输入到已训练好的定性、定量、层次化的深度神经网络诊断模型，通过实际的输出标签值来定性、定量化判断该测试样本所属的故障类型以及故障大小。

具体的，步骤1包括以下步骤：

步骤1.1：对采集到的6000个原始非平稳的轴承振动信号中的任一信号s(t)进行EMD分解，将其分解为有限个平稳的IMF分量，可表示为：

其中，c_a(t),a＝1,2L m代表原始信号经过EMD分解得到的m个平稳的IMF分量，这m个IMF分量分别包含从高频到低频的频率成分。r_m代表分解后的残余项。

步骤1.2：已知采集到的故障信号包含4种类型，任选每种类型中的一个信号，设其各自经过EMD分解得到的第一个IMF分量的离散值用序列表示为c_1z(t)，z＝1,2,3，4，且长度均为N。对每个c_1z(t)建立AR模型可表示为：

其中，p_z(z＝1,2,3，4)代表各个AR模型的阶数，a_zk(k＝1,2L p_z)代表各个模型的p_z个自回归系数，w_z(t)代表各个模型的拟合残差，是均值为0，方差为的白噪声序列。

步骤1.3：利用FPE准则来分别确定4个AR模型的最佳阶数，当准则取最小值时的阶数p_z为各个AR模型的最佳阶数。FPE准则可表示为：

为计算方便，取p_z(z＝1,2,3，4)中的最小值作为所有轴承信号的任一IMF分量建立各自AR模型的标准模型阶数，并记为P。本次实验中，P求得为24，因而对任一一个IMF分量均建立24阶AR模型，以下公式中的P均代表24。

步骤1.4：确定各个AR模型的标准模型阶数P之后，每个AR模型的系统函数均可表示为：

Y＝XA+W (4)

其中：

Y＝[c_P+1 c_P+2 L c_N]^T (5)

A＝[a₁ a₂ L a_P]^T (6)

W＝[w_P+1 w_P+2 L w_N]^T (7)

然后利用最小二乘法求解AR模型的自回归系数A，表示为：

A＝(X^TX)^-1X^TY (9)

方差可用自回归系数表示为：

由于轴承的故障信息主要集中于高频段，因而本发明只考虑原始信号经过EMD分解得到的前4个IMF分量。那么对前4个IMF分量而言，每一个IMF分量所得到的AR模型参数，包括自回归系数以及方差可表示为一个P+1维的向量ARP_e：

对任意一个原始轴承振动信号，可将其前4个IMF分量的AR模型参数转换成特征向量x作为模型的输入，表示为：

考虑到本实例中，AR模型的标准阶数P取24，因而每个原始振动信号经过EMD分解，再提取AR模型参数均可以转换为一个100维的特征向量作为网络的输入，因而可先确定网络的输入单元数为100。

总的来说，步骤1通过EMD分解和AR模型相结合，提取出能反应轴承状态信息的AR模型参数作为网络模型的输入，不但能提高模型的诊断精度，而且将1000维的原始轴承信号降至100维，在接下来的网络训练以及测试过程中大大减小计算量，提高了网络训练以及测试的速度。

具体的，步骤2包括以下步骤：

步骤2.1：重复步骤1.4 6000次，求出每一个轴承信号的100维特征向量作为网络的输入，并将每种轴承状态下样本总数的2/3作为训练样本，另外1/3作为测试样本，那么可得到内圈、滚动体、外圈故障的训练样本数均为1200个，每种故障大小分别包含400个训练样本，正常状态的训练样本数为400个；内圈、滚动体、外圈故障的测试样本数均为600个，每种故障大小分别包含200个测试样本，正常状态的测试样本数为200个。具体的训练以及测试样本数可参考表1。

表1：训练和测试样本数

步骤2.2：利用一个Stacked SAE搭建该发明的第一层网络，用于定性化诊断轴承的故障类型，记为Stacked由表1可知，用于第一层轴承故障定性化诊断的训练样本数G＝4000。在初步确定Stacked的隐藏层数U＝3，每个隐藏层的单元数分别为100,60,10以及每层0.3的学习率情况下，将步骤1.4中得到的训练样本集的特征向量作为输入，那么可通过预训练和微调来确定Stacked每一层的最佳权重矩阵以及偏置项。

(1)预训练的步骤为：

a)对一个含有3个隐藏层的Stacked每一个隐藏层均与上一层构成一个SAE的编码网络。因而，可将输入层和第一个隐藏层视为第一个SAE的编码网络，然后通过反向传播优化算法求得SAE代价函数取得最小值时的权重矩阵和偏置项。假设x^d为训练样本集中的任意一个训练样本，暂不考虑稀疏项，那么自动编码器的代价函数可表示为：

其中，表示该样本x^d经过自动编码器所得到的输出，即自动编码器的重构信号。用L2范数来表示数据保真项。第二项是正则化项，用于抑制权重的幅值，防止过拟合，λ是权重衰减系数，n_l是自动编码器的层数，即为3，S_l是第l层的神经元个数。W＝{W⁽¹⁾,W⁽²⁾}代表自动编码器编码网络与解码网络的权重矩阵，b＝{b⁽¹⁾,b⁽²⁾}代表自动编码器编码网络与解码网络的偏置项，代表第l层的j单元与第l+1层的i单元之间的连接权值。

若对自动编码器加上稀疏惩罚项，则相应的稀疏自动编码器SAE的代价函数可表示为：

其中第一项如式(13)所示，第二项是稀疏惩罚项，β代表稀疏惩罚系数，ρ是一个接近于0的极小值，代表第g个神经元的平均激活值，S₂代表SAE隐藏层的单元数。

利用反向传播算法，通过不断减小代价函数式(14)，当达到指定的迭代次数或者代价函数下降到指定值时，可得到第一个SAE编码网络和解码网络的最佳权重矩阵W₁⁽¹⁾，W₁⁽²⁾以及偏置项那么，对输入样本x^d而言，第一个隐藏层的输出向量h₁^d可表示为：

h₁^d＝f(W₁⁽¹⁾x^d+b₁⁽¹⁾) (15)

其中f是激活函数，本发明采用S型函数，即

b)第一个隐藏层和第二个隐藏层可视为第二个SAE的编码网络，并将第一个隐藏层的输出作为第二个SAE的输入。同样运用反向传播算法，通过不断减小第二个SAE的代价函数，从而得到编码网络和解码网络的最佳权重矩阵以及偏置项那么，第二个隐藏层的输出向量h₂^d可表示为：

c)以此类推，包含3个隐藏层的Stacked需要重复预训练3次，直到第3个SAE预训练完成，并得到编码网络和解码网络的最佳权重矩阵以及偏置项那么第3个隐藏层的输出h₃^d可表示为：

h₃^d＝f(W₃⁽¹⁾h₂^d+b₃⁽¹⁾) (22)

d)网络的输出层可视为一个分类器，输出向量的每一个元素分别对应该样本属于每种类别的概率值。由步骤1已知，采集到的信号一共有4种类型，即B＝4，因而标签可记为1,2，3，4。本发明采用softmax分类器，输入即为第3个隐藏层的输出h₃^d。设输入样本x^d的理想标签是y^d，那么实际的输出向量O^d可表示为:

其中θ表示softmax分类器的权重矩阵，可表示为：

softmax分类器的代价函数可以表示为：

其中，第二项是权重衰减项，用来抑制过拟合。与SAE的预训练类似，softmax分类器的预训练同样是利用反向传播算法求代价函数最小值时的最佳权重矩阵θ。

(2)微调的步骤为：

将预训练步骤得到的3个SAE编码网络的最佳权重矩阵偏置项以及softmax分类器的最佳权重矩阵θ作为Stacked每一层的初始权重矩阵和偏置项，利用反向传播算法再次迭代和更新各个权重矩阵和偏置项，直到达到最大的迭代次数或者softmax分类器的代价函数值下降到指定值，从而获得Stacked每一层最终的最佳权重矩阵θ_f以及偏置项至此，用于轴承故障定性分类的第一层深度神经网络训练完毕。

步骤2.3：同样利用Stacked SAE搭建第二层的故障诊断深度神经网络，用于定量诊断轴承的故障大小。除去正常状态，所采集到的样本信号一共包含3种故障类型，每种故障类型包含3种故障大小，则第二层的定量化诊断网络共需要3个Stacked SAE来分别实现内圈故障、滚动体故障以及外圈故障的定量化诊断，分别记为StackedStackedStacked各种故障大小的标签可记为1,2,3，分别对应的故障大小为0.007英寸，0.014英寸以及0.021英寸，因而各Stacked SAE的输出层数可确定为3。

对第二层的深度神经网络中的每一个Stacked SAE重复执行步骤2.2，在初步确定每个Stacked SAE的隐藏层数U＝3，每个隐藏层的单元数分别为100,60,10以及每层0.3的学习率的情况下，将属于同一种故障类型但是故障大小不同的训练样本集作为输入，那么对于每个Stacked SAE均有1200的训练样本，通过预训练和微调来确定每个Stacked SAE每一层最终的最佳权重矩阵偏置项以及softmax分类器最终的最佳权重矩阵θ_f。至此，用于轴承故障定量诊断的第二层深度神经网络训练完毕。该发明中的每一个Stacked SAE的初始化参数如表2所示。

表2：网络初始化参数

最终，我们可以得到一种基于堆叠稀疏自动编码器(Stacked SAE)深度神经网络的轴承故障定性、定量、层次化诊断方法。网络的第一层用一个Stacked SAE实现4种故障类型的轴承故障定性化分类，包括正常状态以及3种故障状态。第二层用3个Stacked SAE分别实现3种故障类型下3种不同故障严重程度的轴承故障定量化分类，如图5所示。步骤1中所提出的将原始轴承信号经过EMD分解之后提取的AR模型参数作为网络的输入，将1000维的原始轴承信号降低为100维，有利于减小网络训练及测试过程中的计算量。此外，该发明所基于的深度神经网络能进一步自动对输入提取特征并实现自动化诊断，在提高诊断精度的同时大大减少了人力的消耗，即使在大数据时代下也具有重要的实用价值。

具体的，步骤3包括：

步骤3.1：将经过步骤1得到的测试样本集输入到步骤2中已训练好的定性、定量、层次化的轴承故障诊断深度神经网络，先利用第一层的Stacked SAE进行轴承故障定性分类，根据实际输出的标签值来判断该轴承是否存在故障以及故障类型，标签1，2，3，4分别代表内圈故障，滚动体故障，外圈故障以及正常状态。实际的第一层的故障定性化识别结果如图6所示，可见，2000个测试样本中共有6个样本分类错误，精度达到99.7％。每一故障类型正确分类的样本数如表3所示，“in”代表不属于此类的样本被误分为此类，相应的，“out”代表属于此类的样本被误分为其他类。

表3：第一层故障类型的正确分类样本数

步骤3.2：根据第一层的轴承故障定性诊断结果，将标签为1，2，3的测试样本分别输入StackedStackedStacked根据实际的输出标签值来定量化诊断各个测试样本的故障严重程度，标签1，2，3分别代表0.007英寸，0.014英寸和0.021英寸。

第二层的轴承故障定量化识别结果如图7所示，图7(a)代表内圈故障大小的分类情况，精度达到100％。图7(b)，图7(c)分别为滚动体故障大小以及外圈故障大小的分类情况，各自均有1个样本分类错误。因而整个两层的故障诊断网络模型，2000个测试样本中共有8个样本分类错误，精度高达99.6％。具体的分类精度如表4所示。

表4：本发明的故障识别精度

从分析过程和应用实例可以看出，本发明的确能实现高精度的轴承故障定性、定量诊断。此外本发明并不局限于4种轴承状态以及3种故障严重程度的诊断，该实例仅仅用来检验该发明的可靠性。实际应用中，可根据相应的故障类型种类以及故障的严重程度种类改变本发明所基于的深度学习网络模型，具有一定的灵活性。此外，该发明基于的深度神经网络，能够在保证轴承故障定性、定量、层次化诊断精度的前提下，降低对信号处理专业知识的依赖，实现自动提取特征以及自动诊断故障，减少人力的消耗，在大数据时代下更加具有实用价值。

以上所述仅是本发明的优选实施方式，并不用于限制本发明，应当指出，对于本技术领域的普通技术人员来说，在不脱离本发明技术原理的前提下，还可以做出若干改进和变型，这些改进和变型也应视为本发明的保护范围。