一种基于鲁棒SCKF滤波的紧组合导航方法与流程

本发明涉及GPS/SINS组合导航技术领域，特别是一种基于鲁棒SCKF滤波的紧组合导航方法。

二、

背景技术：

GPS/SINS(Global Positioning System/Strap down Inertial Navigation System)组合导航融合了各自的优点，使导航精度高于各系统单独工作的精度。由于导航环境的多变性和复杂性，GPS/SINS组合导航的系统模型往往具有非线性的特点，因此研究应用于组合导航的非线性滤波极为重要。

传统非线性滤波包括扩展卡尔曼滤波(EKF)和无迹卡尔曼滤波(UKF)两种。EKF将非线性函数线性化，会产生截断误差；UKF对非线性系统有较高的滤波精度，但没有严格的数学推导，在滤波的迭代过程中，由于矩阵分解和求逆，难以保证状态协方差矩阵的正定性。平方根容积卡尔曼滤波(SCKF)是一种新兴的非线性滤波方法，由Arasaratnam等人提出。该算法通过严格的数学推证明，基于球面径向规则采取一组权值相等的容积点逼近系统状态的后验分布，可保证协方差矩阵的正定性。同时，传递预测和估计误差协方差阵采用平方差，避免了矩阵分解和求逆运算，保证了其半正定性。该算法被广泛运用于混合滤波、姿态估计和导航制导等领域。

然而，在实际运用中，由于内、外部环境不确定因素的影响，还会发生观测异常等扰动，从而导致较大的估计误差。

三、

技术实现要素：

本发明的目的在于提供一种实时性好、精度高的基于鲁棒SCKF滤波的紧组合导航方法，以消除观测异常对系统的影响并提高组合滤波的性能。

实现本发明目的的技术解决方案为：一种基于鲁棒SCKF滤波的紧组合导航方法，其特征在于，包括以下步骤：

步骤1、通过轨迹发生器、卫星信号模拟器依次模拟生成导弹的IMU数据和GPS中频信号；

步骤2、将模拟生成的IMU数据进行惯导解算，将GPS中频信号注入接收机进行导航解算；

步骤3、建立发射惯性坐标系下GPS/SINS紧组合导航系统模型；

步骤4、在标准平方根容积卡尔曼滤波即SCKF的基础上，引入稳健M，对系统观测噪声阵进行自适应调节，构成鲁棒平方根容积卡尔曼滤波即RSCKF算法，对系统状态进行滤波校正。

本发明与现有技术相比，其显著优点在于：(1)将标准SCKF滤波算法引入组合导航中，符合系统模型的非线性特性，与非线性滤波UKF、CKF相比，避免了矩阵分解和求逆运算，保证了协方差阵的半正定性；(2)将抗差M估计原理引入SCKF滤波中，进一步增强了组合滤波的鲁棒性，提高了在恶劣环境中的组合导航定位精度、跟踪能力。

四、附图说明

图1是本发明基于鲁棒SCKF滤波的紧组合导航方法的流程图。

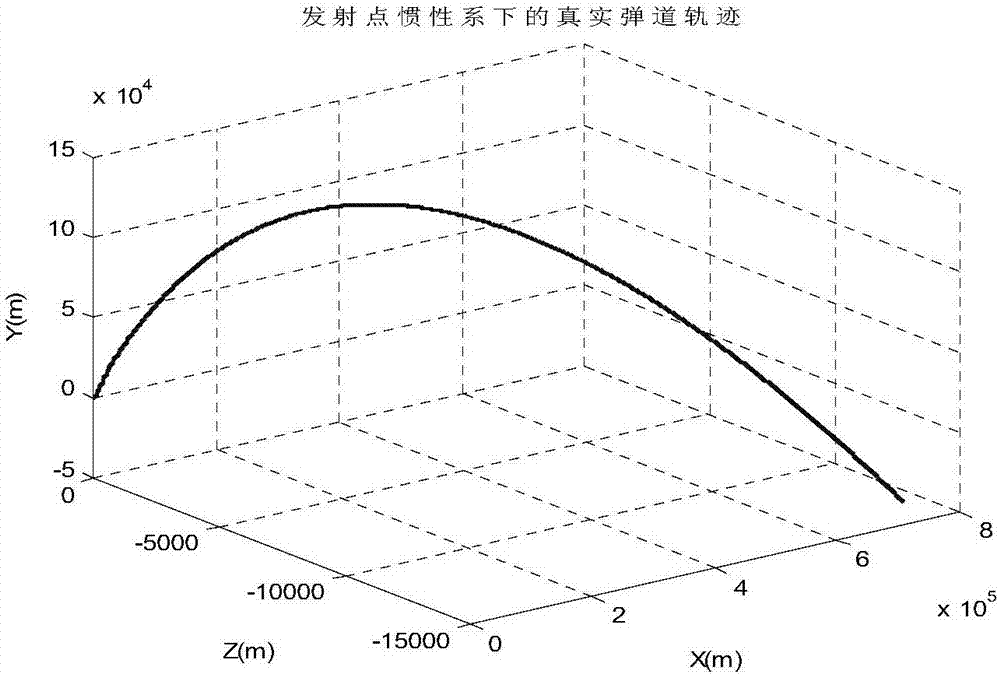
图2是实施例1中由轨迹发生器模拟生成的发射惯性坐标系下的弹道轨迹。

图3是实施例1中鲁棒SCKF与SCKF滤波在X方向的定位误差对比结果。

图4是实施例1中鲁棒SCKF与SCKF滤波在Y方向的定位误差对比结果。

图5是实施例1中鲁棒SCKF与SCKF滤波在Z方向的定位误差对比结果。

五、具体实施方式

下面结合附图及具体实施例对本发明作进一步详细说明。

结合图1，本发明基于强跟踪UKF滤波的GPS/SINS紧组合导航方法，步骤如下：

步骤1、通过轨迹发生器、卫星信号模拟器依次模拟生成导弹的IMU数据和GPS中频信号；

根据弹道导弹飞行的物理模型，设置飞行各阶段的参数，如加速度、角速率变化，可生成导弹的飞行弹道轨迹与相应的IMU数据，将飞行弹道轨迹导入卫星模拟器并处理即可得到相应的GPS中频信号。

步骤2、模拟生成的IMU数据进行惯导解算，将GPS中频信号注入软件接收机进行导航解算；

惯导解算更新弹体的位置、速度、姿态信息；软件接收机导航解算得到弹体位置，卫星位置、伪距信息。

步骤3、建立发射惯性坐标系下GPS/SINS紧组合导航系统模型，具体如下：

(3.1)状态方程：

其中，X_s包含SINS的15个状态误差量；X_g包含GPS的2个状态误差量，具体如下：

其中，为系统的姿态失准角；δV_x、δV_y、δV_z为发射惯性坐标系下三轴方向的速度误差；δX、δY、δZ为发射惯性坐标系下三轴方向的位置误差；ε_x、ε_y、ε_z和分别为陀螺常值漂移、加速度计常值偏置在三轴方向的分量，Δl_u为等效钟差的距离误差，Δl_ru为与钟漂等效的距离率误差；

其中，T_ru为GNSS时钟频率漂移的相关时间，w_u为GNSS时钟误差白噪声；w_ru为GNSS时钟频率误差白噪声；F₁为X、Y、Z三轴比力的反对称矩阵；G_e为观测点到地下矢量的三轴偏导矩阵；为弹体坐标系转换到导航坐标系的转换矩阵；I是单位矩阵；系统的噪声驱动矩阵G_s(t)为：

系统的噪声向量w_s(t)为：

w_s(t)＝[ω_gx ω_gy ω_gz ω_ax ω_ay ω_az]^T

其中，w_gx、w_gy、w_gz分别为陀螺仪在X、Y、Z三轴下的高斯白噪声；w_ax、w_ay、w_az分别为加速度计在X、Y、Z三轴下的高斯白噪声。

(3.2)系统观测方程

发射惯性坐标系下，弹道导弹GPS/SINS深组合导航系统的观测方程分为伪距差和伪距率差两个部分，具体为：

其中：m表示GPS接收机接收到的卫星数目；ρ_I为惯导解算的位置信息计算所得伪距，ρG为GPS接收机测量所得伪距；H(·)为非线性量测函数；v(t)为各元素为零均值的高斯白噪声。

步骤4、在标准平方根容积卡尔曼滤波(SCKF)基础上，引入稳健M，对系统观测噪声阵进行自适应调节，构成鲁棒平方根容积卡尔曼滤波(RSCKF)算法，对系统状态进行滤波校正，具体如下：

首先将步骤3中建立的系统模型进行离散化，得到下式：

式中：X_k∈Rⁿ,Z_k∈R^m分别为k时刻系统的状态向量和量测向量；F_k为线性状态转移矩阵，h(·)为系统非线性量测函数；w_k、v_k为互不相关的零均值高斯白噪声序列，统计特性满足如下条件：

式中：Q_k为非负定矩阵，R_k为正定矩阵；δ_kj为Kronecker-δ函数；

要实现SCKF算法，首先按照三阶容积准则，选取一组2n个等权值分布的容积点{ω_i，ξ_i}实现非线性逼近，其中：

其中：ξ_i为容积点向量；ω_i为对应权重；n为系统状态变量的维数；[l]∈Rⁿ，为生成算子，当n＝2时，表示为如下所示点集：

[l]_i是[l]∈R²中第i列元素；SCKF算法具体步骤如下：

1)滤波初始化

S₀＝chol(P₀)

其中，x₀为系统状态初值；为x₀的均值；P₀为x₀的状态误差协方差阵；上标T为对该矩阵或向量转置，以下同；E(·)为求数学期望；chol(·)表示乔里斯基分解；S₀为P₀的乔里斯基因子。

2)时间更新：

鲁棒平方根容积卡尔曼滤波的时间更新标准平方根卡尔曼滤波一致；

其中，S_k-1为k-1时刻的平方根因子；为k-1时刻的状态向量更新值；为第i个状态容积采样点；u_k-1为系统输入量；f(·)为非线性状态转移函数；为第i个一步预测状态采样值；为加权平均得到的系统状态一步预测值；Tria(·)表示QR分解；S_k|k-1为估计的k时刻平方根因子；矩阵表示为：

3)量测更新：

与标准SCKF量测更新过程一致，仅对噪声矩阵R做出改动：

其中，为量测更新的第i个容积采样点；h(·)为非线性量测函数；为第i个量测值采样点；为量测值采样点加权平均所得的量测估计值；为根据稳健M估计算法对噪声R进行自适应调节后的观测噪声矩阵；矩阵ζ_k|k-1表示为：

估计互协方差矩阵为：

其中，矩阵χ_k|k-1表示为：

S_k＝Tria([χ_k|k-1-K_k·ζ_k|k-1,K_k·S_R,k])

其中，K_k为所求得k时刻的卡尔曼滤波增益；S_k为为经过QR分解的平方根因子；其它参数定义如上。

4)抗差修正R，具体步骤如下：

基于标准SCKF方程，建立抗差SCKF的滤波模型；由于量测信息只影响模型中的量测更新过程，所以相对于标准SCKF算法，鲁棒SCKF算法仅对量测更新方程中的相关表达式进行了调整修正，抗差噪声阵为与R_k等价的量测噪声方差阵，由抗差M估计方法中的等价权矩阵求逆获得，即

此处采用Huber法求取等价权矩阵；设的矩阵元素为i,j＝1,2,…,n，则有如下方法确定等价权矩阵：

其中，分别为等价权矩阵的对角元素与非对角元素；σ_ii,σ_ij为原R_k阵的对角元素和非对角元素；k为常数，通常取1.2～1.5；v_i为观测量z_i的残差分量，为标准残差分量，由得出，其中：

其中，(P_yy,k|k-1)_ii为取P_yy,k|k-1矩阵的i行i列元素；z_k为真实量测值；为上文求得的量测估计值；v_i为观测残差向量v的第i个元素。

将抗差修正得到的代入步骤3)量测更新中，即得到鲁棒平方根容积容积卡尔曼滤波。按照以上步骤，进行滤波后，得到系统中位置、速度、姿态状态量的误差量，再对组合导航的SINS状态进行校正，输出最终的导航结果。

下面结合具体实施例对本发明作进一步详细说明。

实施例1

为了验证本发明提出的鲁棒SCKF滤波方法的有效性与优越性，将此滤波方法运用在弹载GPS/SINS紧组合导航系统中进行仿真，并将仿真导航结果与标准SCKF滤波结果比较。仿真如下：

1)仿真条件

设置弹体初始俯仰为90°，初始滚转角和偏航角均为0°；初始位置为：纬度30.03°，经度109.6°，高度为10m；初始速度：前向为394.8917m/s(地球自转速度)，天向和侧向均为0m/s；发射方位角为90°；陀螺零偏设为10°/h，白噪声设为1°/h；加速度计零偏设为1mg，白噪声设为0.5mg；收星数m＝4。GPS采样频率1HZ，INS采样频率200HZ，滤波周期1s，仿真时间360s。在200s-210s时间段内，使GPS伪距加入白噪声满足均值0，标准差100的高斯分布；GPS伪距率加入白噪声满足均值为0，标准差为1的高斯分布。

设置导弹的弹道轨迹如图2；图3-5分别为标准SCKF和鲁棒SCKF紧组合导航在X、Y、Z三个方向的定位误差。

2)结果分析

图2-图4为分别为经过SCKF、抗差SCKF滤波的组合导航位置误差对比图。可以看出，在初始位置误差最高达到10m，但都能快速收敛。在20s～200s时段，GPS/SINS组合导航系统的量测噪声处于正常状态的情况下，两种滤波算法均能实现导弹的准确定位；在200s～210s时段，由于受到加入的伪距、伪距率观测粗差影响，标准SCKF存在X方向误差[-9.5m，4.1m]，Y方向定位误差[-9.6m，3.8m]，Z方向定位误差[-3.6m，3.8m]，且收敛时间较长；而抗差SCKF滤波的三轴方向误差均保持在[-1.5m，2.1m]区间内，定位结果明显优于标准SCKF算法；在250s～360s时段，标准SCKF滤波收敛，达到与抗差SCKF相当的效果。因此，可得出结论：本发明提出的一种基于鲁棒SCKF滤波的紧组合导航方法，在满足了正常情况下的组合导航工作的同时，减小了观测量异常误差常生的影响，有效改善了滤滤波性能，提高了导航定位精度。