一种基于动态参数的动力电池SOC估算方法及系统与流程

本发明涉及电动汽车和储能电池管理系统领域，特别涉及一种基于动态参数的动力电池SOC估算方法及系统。

背景技术：

目前，国内外关于动力电池荷电状态(State of Charge,SOC)估计方法主要包括：内阻法、安时积分法、开路电压法、卡尔曼滤波法、观测器法、粒子滤波法和神经网络法。其中，内阻法依据电池内阻和SOC之间的函数关系，通过检测电池内阻检测内阻来计算电池SOC，然而在线、准确地测量电池内阻存在因难，限制了该方法在实际工程中的应用。安时积分法虽然原理简单、易于实现，但是无法消除SOC初始误差以及因电流测量不准确而引起的累计误差。开路电压法根据开路电压(OCV)和SOC的对应关系来计算电池SOC，需要将电池充分静置后才能测量OCV，因此不适用于SOC的在线估计。卡尔曼滤波法和观测器法，都能够很好地修正电池SOC的初始误差，且具有良好的抗噪能力，然而它们对模型精度的要求非常高。粒子滤波法，收敛时间过长。神经网络法，需要大量的训练样本，在实际应用中我们不可能得到覆盖所有实际工况的样本数据，因此其精度也将受到一定的影响，而且该方法计算量大难以在硬件中实现。动力电池是是个复杂的非线性动力系统，电池模型参数明显受到温度、电池自放电、老化等诸多因素的影响。

现有的电池SOC估计方法在实际应用中，都不同程度地存在一定不便和缺陷，因此有必要做进一步的改进。

技术实现要素：

本发明的目的在于，解决现有电池SOC估算精度和速度的问题。

为实现上述目的，第一方面，本发明提供了一种基于动态参数的动力电池SOC估算方法及系统，该方法包括以下步骤：对电池开展放电-静置实验，获得电池在不同温度下的OCV-SOC特性曲线，拟合出OCV-SOC的关系表达式；对电池进行恒定电流的脉冲放电-静置实验，记录期间的电压响应，根据所得电压响应曲线，通过离线的方法辨识出电池二阶RC等效电路模型的参数初始值；利用含遗忘因子的递推最小二乘法RRFLS，对二阶RC等效电路模型进行动态参数辨识；采用EKF算法对电池SOC进行在线估算。

优选地，电池二阶RC等效电路模型主要由第一电阻(R₀)、第二电阻(R₁)、第三电阻(R₂)、第一电容(C₁)、和第二电容(C₂)构成。

优选地，遗忘因子的值为0.95～0.98。

第二方面，本发明提供了一种基于动态参数的动力电池SOC估算系统，该系统包括：第一计算模块，用于对电池开展放电-静置实验，获得电池在不同温度下的OCV-SOC特性曲线，拟合出OCV-SOC的关系表达式；第二计算模块，用于对电池进行恒定电流的脉冲放电-静置实验，记录期间的电压响应，根据所得电压响应曲线通过离线的方法辨识出电池二阶RC等效电路模型的参数初始值；第三计算模块，用于利用含遗忘因子的递推最小二乘法RRFLS，对二阶RC等效电路模型进行动态参数辨识；第四计算模块，用于采用EKF算法对电池SOC进行在线估算。

本发明克服了安时积分法中的SOC初值不准确及累计误差的现象，适应电池特性的动态变化，电池模型精度高，收敛速度快，稳定可靠，提高了SOC在线估算的精度，可广泛应用于电动汽车和储能电池管理系统领域。

附图说明

图1是本发明实施例提供的一种基于动态参数的动力电池SOC估算方法流程示意图；

图2是电池二阶RC等效电路模型结构示意图。

具体实施方式

为使本发明实施例的目的、技术方案和优点更加清楚，下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。

为便于对本发明实施例的理解，下面将结合附图以具体实施例做进一步的解释说明，实施例并不构成对本发明实施例的限定。

图1是本发明实施例提供的一种基于动态参数的动力电池SOC估算方法流程示意图。如图1所示，该方法包括以下步骤：

步骤一、对电池开展放电-静置实验，获得电池在不同温度下的OCV-SOC特性曲线，拟合出OCV-SOC的关系表达式。

步骤二、对电池进行恒定电流的脉冲放电-静置实验，记录期间的电压响应，根据所得电压响应曲线，通过离线的方法辨识出电池二阶RC等效电路模型的参数初始值。

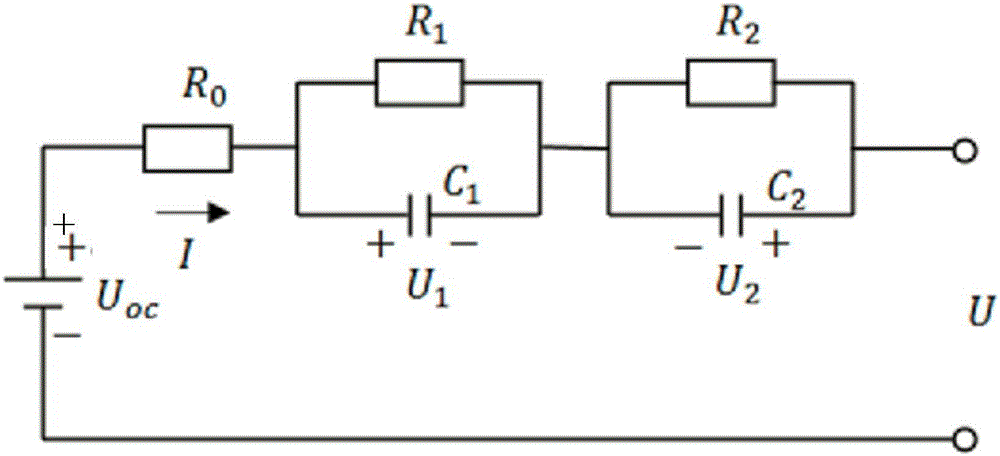
在一个优选的方案中，电池二阶RC等效电路模型如图2所示，该电池二阶RC等效电路模型主要由第一电阻R₀、第二电阻R₁、第三电阻R₂、第一电容C₁、和第二电容C₂构成；其中，U_oc代表电池的开路电压(OCV)；U₁为电池组的端电压；R₀为电池的欧姆内阻；R₁、R₂分别为电池充放电过程中的电化学极化和浓度差极化电阻；C₁、C₂分别为电池充放电过程中的暂态电容效应、电化学极化和浓度差极化电容；U₁、U₂分别为通过电容C₁、C₂的电压值；U为电池端电压；I为电池端电流。

步骤三、利用含遗忘因子的递推最小二乘法RRFLS，对二阶RC等效电路模型进行参数辨识。优选地，遗忘因子的值为0.95～0.98。

具体地，由基尔霍夫定律与拉布拉斯变换，得到二阶RC等效电路模型频域下的状态方程为：

令时间常数τ₁＝R₁C₁，τ₂＝R₂C₂；

则上式可化简为：

τ₁τ₂U_ocs²+(τ₁+τ₂)U_ccs+U_cc＝τ₁τ₂IR₀s²+Is|R₁τ₂+R₂τ₁+R₀(τ₁+τ₂)|+I(R₁+R₂+R₀)+τ₁τ₂Us²+(τ₁+τ₂)Us+U

设a＝τ₁τ₂，b＝τ₁+τ₂，c＝R₁+R₂+R₀，d＝R₁τ₂+R₂τ₁+R₀(τ₁+τ₂)

则上式可简化为：

aU_ocs²+bU_ocs+U_oc＝aR₀Is²+dIs+cI+aUs²+bUs+U；

将上式进行离散化处理，其中T为采样时间，整理可得：

U_oc(k)-U＝k₁|U(k-1)-U_oc(k-1)|+k₂|U(k-2)-U_oc(k-2)|+k₃I(k)+k₄I(k-1)+k₅I(k-2)

其中，

式中，即可代入递推最小二乘的辨识方法中，当前时刻的θ＝|k₁k₂k₃k₄k₅|^T值，然后根据以下公式：

R₀＝k₅/k₂

R₁＝(τ₁c+τ₂R_i-d)/(τ₁-τ₂)

R₂＝(c-R₁-R_i

C₁＝τ₁/R₁

C₂＝τ₂/R₂

计算出二阶RC等效电路模型参数R₀、R₁、R₂、C₁、C₂，从而实现模型参数的动态辨识。

步骤四、采用EKF算法对电池SOC进行在线估算，EKF算法全称ExtendedKalman Filter，即扩展卡尔曼滤波器，一种高效率的递归滤波器(自回归滤波器)。

具体地，根据所选取的二阶RC等效电路模型，得到电池的状态方程和量测方程如下：

状态方程离散化后的离散模型:

令电池模型中的状态变量为x＝[x₁ x₂ x₃]＝[U_oc U₁ U₂]^T，系统输入u为锂离子电池的工作电流I，且放电为正，系统输出y为锂离子电池的工作电压U，采样时间为T。

锂离子电池离散状态空间模型为：

其中

D_k＝-R₀(K)

算法系统参数状态量初始化

x₀＝[SOC(0) 0 0]^T

运行扩展卡尔曼滤波算法

预测模块：

(1)状态预测：

(2)状态预测误差协方差矩阵：

纠错模块：

(1)卡尔曼增益：

其中，

(2)状态估计：

(3)状态估计误协方差矩阵：

P_k＝(I-G_kC_k)P_k|k-1

其中，P_k为协方差；G_k为卡尔曼增益；Q_k-1为过程噪声误差；R_k-1为观测噪声误差。

步骤五、由SOC估算值，根据步骤一所获得的OCV-SOC特性曲线，得到k时刻的开路电压值U_oc，利用RRFLS算法得求到k时刻的θ＝|k₁k₂k₃k₄k₅|^T值，再计算出k时刻模型参数值R₀、R₁、R₂、C₁、C₂；

步骤六：实时更新EFK算法中状态方程的参数值Ak、Bk、Ck、Dk，然后再运行扩展卡尔曼滤波算法，得到k+1时刻的SOC估计值，然后返回步骤四。

通过步骤六计算更新模型参数和步骤五估算SOC这两个循环步骤，将每一次经过得到的SOC和时刻模型参数值R₀、R₁、R₂、C₁、C₂代入离散状态空间方程得到新的预测值，通过不断的预测和修正的递推方式进行计算，便可以递推得到锂电池模型的实时参数值和当前的SOC估算值，使最终的SOC和模型参数值R₀、R₁、R₂、C₁、C₂滤波结果不断趋近于电池的实际情况。

相应地，本发明实施例提供了一种基于动态参数的动力电池SOC估算系统，该系统包括：

第一计算模块，用于对电池开展放电-静置实验，获得电池在不同温度下的OCV-SOC特性曲线，拟合出OCV-SOC的关系表达式；

第二计算模块，用于对电池进行恒定电流的脉冲放电-静置实验，记录期间的电压响应，根据所得电压响应曲线，通过离线的方法辨识出电池二阶RC等效电路模型的参数初始值；

第三计算模块，用于利用含遗忘因子的递推最小二乘法RRFLS，对二阶RC等效电路模型进行动态参数辨识；

第四计算模块，用于采用EKF算法对电池SOC进行在线估算。

本发明实施例克服了安时积分法中的SOC初值不准确及累计误差的现象，适应电池特性的动态变化，电池模型精度高，收敛速度快，稳定可靠，提高了SOC在线估算的精度，可广泛应用于电动汽车和储能电池管理系统领域。

以上对本发明进行了详细介绍，并结合具体实施例对本发明做了进一步阐述，必须指出，以上实施例的说明不用于限制而只是用于帮助理解本发明的核心思想，对于本技术领域的普通技术人员来说，在不脱离本发明原理的前提下，对本发明进行的任何改进以及与本产品等同的替代方案，也属于本发明权利要求的保护范围内。