由小尺寸试件确定无尺寸效应的混凝土起裂韧度的方法与流程

本发明属于土木与水利工程材料性能技术领域，具体涉及由小尺寸试件确定无尺寸效应的混凝土起裂韧度的方法。

背景技术：

带裂缝的混凝土试件的起裂荷载对应的应力强度因子，即为其起裂韧度大量研究表明，混凝土的起裂韧度存在明显的尺寸效应。若要得到与试件尺寸无关的起裂韧度，则须浇筑较大尺寸试件；比如对骨料粒径在10mm-40mm的试件，三点弯曲或者楔入劈拉试件的高度d需达到600mm或超过1000mm。若采用小尺寸试件，则起裂韧度的尺寸效应又不可避免。如何由处于弹塑性断裂条件下的小尺寸试件(比如试件高度d＝100mm-400mm的试件)，来确定无尺寸效应的混凝土真实起裂韧度，是亟待解决的科学难题。

技术实现要素：

目前，测定无尺寸效应的混凝土起裂韧度需要的试件尺寸较大，普通实验室条件下较难完成试样的浇筑和测试工作。若采用小尺寸试件，则起裂韧度的尺寸效应又不可避免。为克服现有测定方法的不足，本发明提供一种由小尺寸试件确定无尺寸效应的混凝土起裂韧度的方法。

本发明的目的是以下述方式实现的：

一种由小尺寸试件确定无尺寸效应的混凝土起裂韧度的方法，包括以下步骤：

(1)按给定的混凝土配合比要求，制作一定数量的尺寸为d×b×l的混凝土试件，其中，d为试件高度，b为试件厚度，l为试件有效跨度；

(2)在普通的压力试验机或者万能试验机上，按静力加载试验方法加载，试验过程中记录每个试件的起裂荷载pini；

(3)基于步骤(2)所得的每个试件的起裂荷载pini，计算出每个试件的名义强度σn；

(4)计算出每个试件的几何参数a；

(5)基于由外推法确定无尺寸效应的无限大板参数的方法，将步骤(3)、步骤(4)所得的不同试件的σn与相应的a值，带入下式(1)进行回归分析：

即可得出无尺寸效应的混凝土的起裂韧度以及初裂强度

在所述步骤(3)中，对三点弯曲梁试件，名义强度σn(pini)的计算公式为：

对楔入劈拉试件，名义强度σn(pini)的计算公式为：

其中，pini为实测各试件起裂荷载；d为试件高度；l为试件有效跨度；b为试件厚度；a0为初始裂缝长度。

步骤(1)中，试件选取的方式为：采用具有相同试件高度d但初始裂缝长度a0不同的试件，试件初始缝高比α选择3-6种，每个初始缝高比α对应2-4个试件，其中试件的初始缝高比α＝a0/d为0.10、0.15、0.2、0.25、0.3、0.35、0.4、0.45、0.5、0.55、0.6、0.65或0.70。

步骤(1)中，试件选取的方式为：采用具有相同初始缝高比α，但试件高度d不同的试件，试件高度d选择3-6种，每个试件高度d对应2-4个试件，其中试件的初始缝高比α＝a0/d＝0.20-0.60。

所述步骤(4)中几何参数a的计算方法为：

(1)对于三点弯曲梁试件，几何参数a由下式(3a)-(3d)计算：

a＝0.8[(1-α)²×b(α)]²×a0式(3a)；

当l/d＝2.5时，

当l/d＝4时，

当l/d＝8时，b(α)＝1.106-1.552α+7.71α²-13.53α³+14.23α⁴式(3d)；

当l/d为其他值时，可按线性插值的方法处理求解；

(2)对楔入劈拉试件，几何参数a由下式(4a)-(4b)计算：

其中，α为缝高比，α＝a0/d；a0为初始裂缝长度；b(α)为几何影响参数。

本发明的有益效果在于：现有测定无尺寸效应的混凝土起裂韧度需要的试件尺寸较大，普通实验室条件下较难完成试样的浇筑和测试工作。若采用小尺寸试件，则起裂韧度的尺寸效应又不可避免。而本发明的方法形式简单，试验易操作，具有足够精度，且易判断结果合理性。本发明基于渐进外推的思想，及弹塑性断裂力学理论分析，由有限尺寸试件的试验数据，外推出无限大板试件的材料参数(无限大板的材料参数无尺寸效应)。因此，只需由小尺寸试件的起裂荷载，即可确定无尺寸效应的混凝土起裂韧度不需要满足现行国内外规范对试验试样尺寸、型式，加载条件等的严格规定，并且双边拉伸试件在试验过程中的稳定性又好于单边拉伸试件，更易于操作。

附图说明

图1是实施例1由相同试件尺寸而不同缝高比的三点弯曲梁试件确定混凝土起裂韧度的示意图。

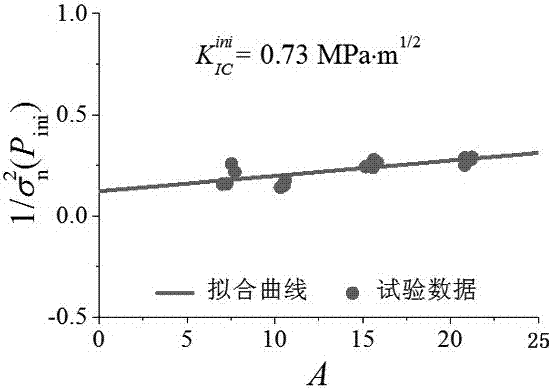
图2是实施例2由不同试件尺寸而相同缝高比的三点弯曲梁确定混凝土起裂韧度的示意图。

图3是实施例3由相同试件尺寸而不同缝高比的楔入劈拉试件确定的混凝土起裂韧度的示意图。

图4是实施例4由不同试件尺寸而相同缝高比的楔入劈拉试件确定混凝土起裂韧度的示意图。

具体实施方式

下面结合附图和实施例来说明本发明的具体实施方式，但以下实施例只是用来详细说明本发明，并不以任何方式限制本发明的范围。

一种由小尺寸试件确定无尺寸效应的混凝土起裂韧度的方法，包括以下步骤：

(1)按给定的混凝土配合比要求，制作一定数量的尺寸为d×b×l的混凝土试件，其中，d为试件高度，b为试件厚度，l为试件有效跨度；

(2)在普通的压力试验机或者万能试验机上，按静力加载试验方法加载，试验过程中记录每个试件的起裂荷载pini；

(3)基于步骤(2)所得的每个试件的起裂荷载pini，计算出每个试件的名义强度σn；

(4)计算出每个试件的几何参数a；

(5)基于由外推法确定无尺寸效应的无限大板参数的方法，将步骤(3)、步骤(4)所得的不同试件的σn与相应的a值，带入下式(1)进行回归分析：

即可得出无尺寸效应的混凝土的起裂韧度以及初裂强度

在所述步骤(3)中，对三点弯曲梁试件，名义强度σn(pini)的计算公式为：

对楔入劈拉试件，名义强度σn(pini)的计算公式为：

其中，pini为实测各试件起裂荷载；d为试件高度；l为试件有效跨度；b为试件厚度；a0为初始裂缝长度。

步骤(1)中，试件选取的方式为：采用具有相同试件高度d但初始裂缝长度a0不同的试件，试件初始缝高比α选择3-6种，每个初始缝高比α对应2-4个试件，其中试件的初始缝高比α＝a0/d为0.10、0.15、0.2、0.25、0.3、0.35、0.4、0.45、0.5、0.55、0.6、0.65或0.70。

步骤(1)中，试件选取的方式为：采用具有相同初始缝高比α，但试件高度d不同的试件，试件高度d选择3-6种，每个试件高度d对应2-4个试件，其中试件的初始缝高比α＝a0/d＝0.20-0.60。

所述步骤(4)中几何参数a的计算方法为：

(1)对于三点弯曲梁试件，几何参数a由下式(3a)-(3d)计算：

a＝0.8[(1-α)²×b(α)]²×a0式(3a)；

当l/d＝2.5时，

当l/d＝4时，

当l/d＝8时，b(α)＝1.106-1.552α+7.71α²-13.53α³+14.23α⁴式(3d)；

当l/d为其他值时，可按线性插值的方法处理求解；

(2)对楔入劈拉试件，几何参数a由下式(4a)-(4b)计算：

其中，α为缝高比，α＝a0/d；a0为初始裂缝长度；b(α)为几何影响参数。

实施例1：

本实施例1试验所用试件为相同试件尺寸不同缝高比的混凝土，其尺寸l×b×d＝320×40×80mm，初始缝高比α＝a0/d＝0.3-0.6。

基于实测的起裂荷载pini，由式(2a)可计算出每个试件的名义强度σn(pini)，由式(3a)-(3d)计算每个试件的几何参数a，得到不同的σn(pini)与a后，带入式(1)进行回归分析，即可得出混凝土的起裂韧度

实施例1试验数据回归确定的混凝土起裂韧度结果参见图1。

由本发明方法确定起裂韧度为0.69mpa·m^1/2，与由双k理论计算的起裂韧度0.71mpa·m^1/2相吻合。

实施例2：

本实施例2试验所用试件为相同缝高比而不同试件尺寸的混凝土，初始缝高比α＝a0/d＝0.5，其尺寸l×b×d依次为：600×200×150mm，800×200×200mm，1200×200×300mm，1600×200×400mm。

基于实测的起裂荷载pini，由式(2a)可计算出每个试件的名义强度σn(pini)，由式(3a)-(3d)计算每个试件的几何参数a，得到不同的σn(pini)与a后，带入式(1)进行回归分析，即可得出混凝土的起裂韧度

实施例2试验数据回归确定的混凝土起裂韧度结果参见图2。

由本发明方法确定起裂韧度0.73mpa·m^1/2，与由双k理论计算的起裂韧度0.67mpa·m^1/2基本吻合。

实施例3：

本实施例3试验所用试件为相同缝高比而不同试件尺寸的混凝土，初始缝高比α＝a0/d＝0.5，其试件高度d依次为：100mm，200mm，300mm，400mm,厚度b为统一值100mm。

基于实测的起裂荷载pini，由式(2b)可计算出每个试件的名义强度σn(pini)；由式(4a)-(4b)计算每个试件的几何参数a。得到不同的σn(pini)与a后，带入式(1)进行回归分析，即可得出混凝土的起裂韧度

实施例3试验数据回归确定的混凝土起裂韧度结果参见图3。

由本发明方法确定起裂韧度0.66mpa·m^1/2，与由双k理论计算的起裂韧度0.42-0.68mpa·m^1/2相吻合。

实施例4：

本实施例4试验所用试件为相同试件尺寸不同缝高比的混凝土，其试件高度d＝200mm，厚度b＝200mm,初始缝高比α＝a0/d＝0.3-0.6。

基于实测的起裂荷载pini，由式(2b)可计算出每个试件的名义强度σn(pini)；由式(4a)-(4b)计算每个试件的几何参数a，得到不同的σn(pini)与a后，带入式(1)进行回归分析，即可得出混凝土的起裂韧度

实施例4试验数据回归确定的混凝土起裂韧度结果参见图4。

由本发明方法确定起裂韧度为0.61mpa·m^1/2，与由双k理论计算的起裂韧度0.50-0.62mpa·m^1/2相吻合。

对所公开实施例的上述说明，使本领域技术人员能够实现或使用本发明。对这些实施例的多处修改对本领域技术人员来说是显而易见的，本文中所定义的一般原理可以在不脱离发明的精神或范围的前提下，在其它实施例中实现。因此，本发明将不限制于本文所显示的这些实施例，而是要符合与本文公开原理和新颖特点相一致的最宽范围。