一种剧烈起伏自由地表有限差分正演模拟系统及方法与流程

本发明属于石油勘探领域，具体涉及一种剧烈起伏自由地表有限差分正演模拟系统及方法。

背景技术：

剧烈的起伏地表广泛地存在于中国地区。地震勘探的前缘正逐步向复杂地表地区转移，常规的处理和解释方法对上述复杂起伏地表已经不再适用。为了更好地解决勘探开发难题，须密切研究起伏地表条件下介质地震波正演模拟，对于起伏地表条件下的地质构造进行正演模拟，可从数值模拟结果中认识、分析地震波波场特征及地震波传播规律等，更好地指导后续的地震勘探。

有限差分方法因其计算速度快、占用内存低、容易实现等优点得到广泛应用，但有限差分方法是基于矩形网格剖分的，因此在处理起伏地表时存在很大的缺陷，在模拟地震波传播时会产生明显的绕射噪音及不稳定。一种常用的解决方法是对物理模型进行曲网格剖分，并将物理域的曲网格变换为矩形网格，但该方法也存在一定的局限性，该方法对稳定性的要求较高，无法处理剧烈的起伏地表。

技术实现要素：

针对现有技术中存在的上述技术问题，本发明提出了一种剧烈起伏自由地表有限差分正演模拟系统及方法，设计合理，克服了现有技术的不足，具有良好的效果。

为了实现上述目的，本发明采用如下技术方案：

一种剧烈起伏自由地表有限差分正演模拟系统，包括模型输入模块、正演模拟模块、速度场转换模块、波场计算模块、波场存储模块、波场反变换模块以及结果输出模块；

模型输入模块，被配置为用于输入速度场和起伏地表的高程；

正演模拟模块，被配置为用于进行剧烈起伏自由地表有限差分正演模拟；

速度场转换模块，被配置为用于将速度场变换到矩形网格坐标系下；

波场计算模块，被配置为用于在过渡坐标系下更新地下区域波场以及在过渡坐标系下采用自由地表边界条件更新地表波场；

波场存储模块，被配置为用于在矩形网格坐标系下存储波场；

波场反变换模块，被配置为用于将波场变换到笛卡尔坐标系下；

结果输出模块，被配置为用于输出最终的波场快照和炮记录。

此外，本发明还提到一种剧烈起伏自由地表有限差分正演模拟方法，该方法采用如上所示的一种剧烈起伏自由地表有限差分正演模拟系统，包括如下步骤：

步骤1：通过模型输入模块输入速度场和起伏地表的高程，建立观测系统；

步骤2：通过速度场转换模块采用如下所示的变换方程将速度场变换到矩形网格坐标系下；

其中，x和z为笛卡尔坐标下的空间坐标，ξ和η为矩形网格坐标系下的空间坐标，z₀(ξ)为笛卡尔坐标系下的高程函数，η_max为矩形网格坐标系下的最大采样点数；

步骤3：引入过渡坐标系，通过波场计算模块在过渡坐标系下采用如下所示的一阶速度-应力弹性波方程更新地下区域波场；

其中，u_x和u_z分别为水平分量和垂直分量的速度，τ_xx和τ_zz是正应力，τ_xz是切应力，t是时间；λ和μ是拉梅常数，ρ是密度；系数A和B由下式求得：

步骤4：通过波场计算模块在过渡坐标系下采用如下所示的自由地表边界条件更新地表波场；

其中，C-J八个系数可由下式求得：

步骤5：通过波场存储模块在矩形网格坐标系下存储区域波场和地表波场；

步骤6：通过波场反变换模块将区域波场和地表波场变换到笛卡尔坐标系下；

步骤7：通过结果输出模块输出最终的波场快照和炮记录。

优选地，对步骤3中过渡坐标系下的一阶速度-应力弹性波方程的推导过程如下：笛卡尔坐标系下的一阶速度-应力弹性波方程为：

应用链式法则，(2)式可变换为

对于方程(3)，我们需要计算和可由下式求得

方程(4)变换得到方程(5)

由映射方程

可得

将方程(7)代入方程(5)可得

将方程(8)带入方程(3)，得到过渡坐标系下的一阶速度-应力方程如方程(9)所示。

优选地，对步骤4中过渡坐标系下的自由地表边界条件的推导过程如下：

笛卡尔坐标系下的自由地表边界条件为：

其中

将方程(11)代入到方程(10)中可得

对方程(12)应用链式法则可得

在起伏地表处

将方程(14)代入方程(13)可得

整理方程(15)可得

本发明所带来的有益技术效果：

本发明能够对剧烈起伏地表进行准确模拟的有限差分正演模拟，通过引入过渡坐标系和矩形网格坐标系，在三个坐标系之间进行转换，既能克服传统传统有限差分方法在处理起伏地表时的缺陷，又能保持有限差分方法的精度，而不明显增加计算量，开发剧烈起伏自由地表有限差分正演模拟方法，为研究剧烈起伏地表地区的波场传播规律提供了理论基础，同时，为剧烈起伏地表地区的采集数据进行后续成像和反演工作提供了高精度的地震波正演基础。

附图说明

图1为本发明一种剧烈起伏自由地表有限差分正演模拟方法的流程图。

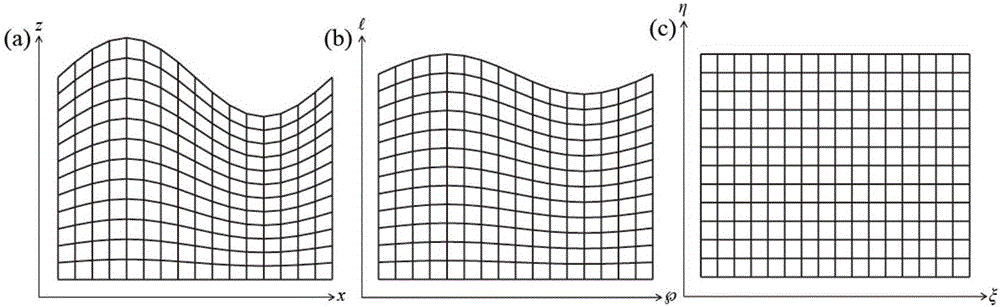
图2为三个坐标系网格示意图，其中，图(a)为笛卡尔坐系网格示意图；图(b)为过渡坐标系网格示意图；图(c)为矩形网格坐标系网格示意图。

图3为加拿大逆掩断层速度模型示意图，其中，图(a)为纵波速度模型示意图；图(b)为横波速度模型示意图。

图4为起伏地表高程函数示意图。

图5为加拿大逆掩断层网格剖分图，其中，图(a)为笛卡尔坐标系网格剖分图；图(b)为过渡坐标系网格剖分图。

图6为采用本发明方法得到的波场快照图，其中，图(a)为0.625s水平分量的波场快照图；图(b)为0.625s垂直分量的波场快照图；图(c)为0.7s水平分量的波场快照图；图(d)为0.7s垂直分量的波场快照图。

图7为采用传统方法得到的波场快照图，其中，图(a)为0.625s水平分量的波场快照图；图(b)为0.625s垂直分量的波场快照图；图(c)为0.7s水平分的波场快照图量；图(d)为0.7s垂直分量的波场快照图。

图8为采用本发明方法得到的炮记录。

图9为本发明一种剧烈起伏自由地表有限差分正演模拟系统的结构示意图。

具体实施方式

下面结合附图以及具体实施方式对本发明作进一步详细说明：

实施例1

如图9所示，一种剧烈起伏自由地表有限差分正演模拟系统，包括模型输入模块、正演模拟模块、速度场转换模块、波场计算模块、波场存储模块、波场反变换模块以及结果输出模块；

模型输入模块，被配置为用于输入速度场和起伏地表的高程；

正演模拟模块，被配置为用于进行剧烈起伏自由地表有限差分正演模拟；

速度场转换模块，被配置为用于将速度场变换到矩形网格坐标系下；

波场计算模块，被配置为用于在过渡坐标系下更新地下区域波场以及在过渡坐标系下采用自由地表边界条件更新地表波场；

波场存储模块，被配置为用于在矩形网格坐标系下存储波场；

波场反变换模块，被配置为用于将波场变换到笛卡尔坐标系下；

结果输出模块，被配置为用于输出最终的波场快照和炮记录。

实施例2

在上述实施例的基础上，本发明还提到一种剧烈起伏自由地表有限差分正演模拟方法，其流程图如图1所示，包括如下步骤：

步骤1：通过模型输入模块输入速度场和起伏地表的高程，建立观测系统；

步骤2：通过速度场转换模块采用如下所示的变换方程将速度场变换到矩形网格坐标系下；

其中，x和z为笛卡尔坐标下的空间坐标，ξ和η为矩形网格坐标系下的空间坐标，z₀(ξ)为笛卡尔坐标系下的高程函数，η_max为矩形网格坐标系下的最大采样点数；

步骤3：引入过渡坐标系，通过波场计算模块在过渡坐标系下采用如下所示的一阶速度-应力弹性波方程更新地下区域波场；

其中，u_x和u_z分别为水平分量和垂直分量的速度，τ_xx和τ_zz是正应力，τ_xz是切应力，t是时间；λ和μ是拉梅常数，ρ是密度；系数A和B由下式求得：

步骤4：通过波场计算模块在过渡坐标系下采用如下所示的自由地表边界条件更新地表波场；

其中，C-J八个系数可由下式求得：

步骤5：通过波场存储模块在矩形网格坐标系下存储区域波场和地表波场；

步骤6：通过波场反变换模块将区域波场和地表波场变换到笛卡尔坐标系下；

步骤7：通过结果输出模块输出最终的波场快照和炮记录。

优选地，对步骤3中过渡坐标系下的一阶速度-应力弹性波方程的推导过程如下：

笛卡尔坐标系下的一阶速度-应力弹性波方程为：

应用链式法则，(2)式可变换为

对于方程(3)，我们需要计算和可由下式求得

方程(4)变换得到方程(5)

由映射方程

可得

将方程(7)代入方程(5)可得

将方程(8)带入方程(3)，得到过渡坐标系下的一阶速度-应力方程如方程(9)所示。

优选地，对步骤4中过渡坐标系下的自由地表边界条件的推导过程如下：

笛卡尔坐标系下的自由地表边界条件为：

其中

将方程(11)代入到方程(10)中可得

对方程(12)应用链式法则可得

在起伏地表处

将方程(14)代入方程(13)可得

整理方程(15)可得

图2为三个坐标系网格示意图，图(a)笛卡尔坐系网格示意图；图(b)过渡坐标系网格示意图；图(c)矩形网格坐标系网格示意图；

本发明一种剧烈起伏自由地表有限差分正演模拟方法，应用于国际标准的起伏地表加拿大逆掩断层模型(如图3所示)，取得了理想的计算效果。输入速度场和起伏地表的高程(如图4所示)，建立观测系统；将速度场变换到矩形网格坐标系下(如图5b所示)；引入过渡坐标系，在过渡坐标系下(如图5a所示)更新地下区域波场；在过渡坐标系下采用自由地表边界条件更新地表波场(如图6所示)；在矩形网格坐标系下存储波场；将波场变换到笛卡尔坐标系下；输出最终的波场快照和炮记录(如图8所示)。本发明的剧烈起伏自由地表有限差分正演模拟方法所得的波场快照(如图6所示)，波形清晰，没有出现绕射噪音和不稳定现象。而传统有限差分方法得到的波场快照(如图7所示)出现了明显的不稳定。

本发明能够对剧烈起伏地表进行准确模拟的有限差分正演模拟，通过引入过渡坐标系和矩形网格坐标系，在三个坐标系之间进行转换，既能克服传统传统有限差分方法在处理起伏地表时的缺陷，又能保持有限差分方法的精度，而不明显增加计算量，开发剧烈起伏自由地表有限差分正演模拟方法，为研究剧烈起伏地表地区的波场传播规律提供了理论基础，同时，为剧烈起伏地表地区的采集数据进行后续成像和反演工作提供了高精度的地震波正演基础。

当然，上述说明并非是对本发明的限制，本发明也并不仅限于上述举例，本技术领域的技术人员在本发明的实质范围内所做出的变化、改型、添加或替换，也应属于本发明的保护范围。