一种基于磁梯度不变量的磁梯度计校正方法与流程

技术领域：
：本发明涉及一种地球物理勘探中的磁测仪器的校正，尤其是基于磁梯度不变量的磁梯度计校正方法。
背景技术：
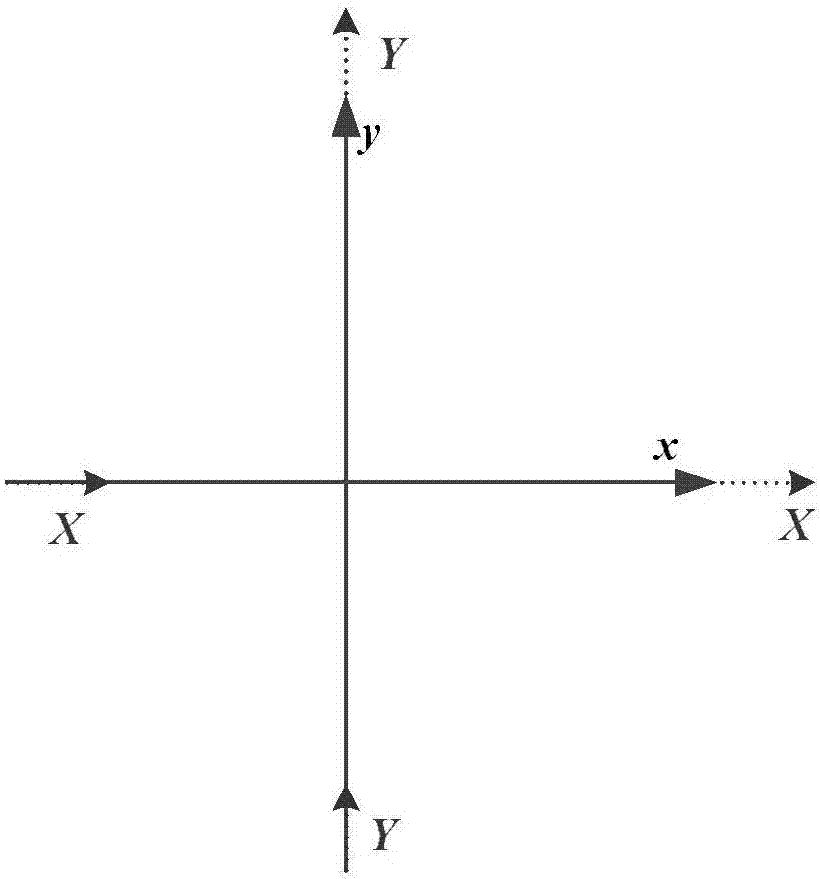
：：在地球磁场下进行磁场相关的科学研究和生产实践，已经从早期的磁场总场和磁场矢量测量发展到现在的磁梯度张量测量。磁梯度计是用来测量磁场空间梯度的装置[pedersenlb,rasmussentm.thegradienttensorofpotentialfieldanomalies:someimplicationsondatacollectionanddataprocessingofmaps.geophysics,1990,55(12):1558-1566.]。磁梯度张量仪具有以下优点：没有磁场测量中对环境磁场方向极度敏感的问题[heathp,heinsong,greenhalghs.somecommentsonpotentialfieldtensordata.explorationgeophysics,2003,34(2):57-62.]，具有更高的目标分辨能力和更加丰富的信息[schmidtpw,clarkda.themagneticgradienttensor:itspropertiesandusesinsourcecharacterization.theleadingedge,2006,25(1):75-78.]。因此被用于地面或水下未爆炸物检查[peiyh,yeohg,kangxy,etal.magneticgradiometeronanauvforburiedobjectdetection,oceans2010.ieee,2010:1-8.]、移动磁性目标探测[narat,suzukis,andos.aclosed-formformulaformagneticdipolelocalizationbymeasurementofitsmagneticfieldandspatialgradients.ieeetransactionsonmagnetics,2006,42(10):3291-3293.]、航空或地面的矿产探查[clarkda,schmidtpw,cowardda,etal.remotedeterminationofmagneticpropertiesandimproveddrilltargetingofmagneticanomalysourcesbydifferentialvectormagnetometry(dvm).explorationgeophysics,1998,29(3/4):312-319.]，火山活动监测[brackenre,grovertp,puniwaigs.developmentandtestingofatensormagneticgradiometersystemwithtrialmonitoringnearthekilaueavolcano,hawaii.usdept.oftheinterior,usgeologicalsurvey,1998.]，地磁图的修正[schifflerm,queitschm,schneiderm,etal.calculationandanalysisofmagneticgradienttensorcomponentsofglobalmagneticmodels.agufallmeetingabstracts.2014,1:03.]，非屏蔽环境中磁纳米粒子的检查[elrefaial,sasadai,yoshidat.fluxgategradiometerformagneticnanoparticlemagnetorelaxometryinunshieldedenvironment,magneticsconference(intermag).2015ieee.ieee,2015:1-1.]，消除探测引力波的飞船的磁干扰[griffindk,massegliao,hallm,etal.designandcalibrationofacompactlow-noisemagneticgradiometer.aerospaceemc,2012proceedingsesaworkshopon.ieee,2012:1-6.]，磁环境评估[voigtj,knappe-grünebergs,gutkelchd,etal.developmentofavector-tensorsystemtomeasuretheabsolutemagneticfluxdensityanditsgradientinmagneticallyshieldedrooms.reviewofscientificinstruments,2015,86(5):055109.]等。磁梯度张量仪按测量原理主要可以分为三种：差分近似法、旋转调制法[tilbrookdl.rotatingmagnetictensorgradiometryandasuperconductingimplementation.superconductorscienceandtechnology,2009,22(7):075002.]、直线测量法[sunderlanda,jul,blairdg,etal.optimizingadirectstringmagneticgradiometerforgeophysicalexploration.reviewofscientificinstruments,2009,80(10):104705.]。其中差分近似法的测量原理最为简单，且可以测量全部的张量元素，因此成为磁梯度张量的主流测量方法。由于需要矢量敏感的传感器，因此主要有基于低温或高温超导量子干涉器件的张量仪[stolzr,zakosarenkov,schulzm,etal.magneticfull-tensorsquidgradiometersystemforgeophysicalapplications.theleadingedge,2006,25(2):178-180.]和以磁通门为核心张量仪[suiy,lig,wangs,etal.compactfluxgatemagneticfull-tensorgradiometerwithsphericalfeedbackcoil.reviewofscientificinstruments,2014,85(1):014701.]。前者在传感器级别已经形成梯度值，后者需要先测量磁场后再做差分。由于地球磁场的存在，目前适合野外应用的磁梯度张量仪校正方法都是利用地球磁场来获取校正参数。其基本思想是如果磁梯度张量仪存在误差，那么在磁场均匀的区域，磁梯度张量仪的输出gik必然是磁场的函数[schifflerm,queitschm,stolzr,etal.calibrationofsquidvectormagnetometersinfulltensorgradiometrysystems.geophysicaljournalinternational,2014,198(2):954-964.]。这样把磁梯度张量仪在均匀磁场中旋转，并且同时测量旋转时的磁场值，就可以利用最小二乘等方法获得校正系数。这类方法有两个主要的问题：第一，在磁场均匀区域内，单个梯度分量为零是磁梯度张量仪校正方法中的必要条件，不能保证各个梯度分量形成张量后作为整体的正确性。特别是对那些能够直接测量梯度的张量仪，此方法仍停留在校正传感器梯度不平衡度的阶段上。第二，作为参考的磁场矢量仪由于存在标度因子误差、非正交误差、安装误差和零偏等，同样需要严格地校正。现有的磁矢量校正往往又需要磁标量作为参考，这一方面造成校正过程复杂，参与设备众多，另一方面使得张量仪的性能受辅助测量仪器性能的制约。目前总体上来说，磁梯度张量仪的校正可以划分为两个阶段：第一个阶段是校正梯度张量中的每个分量；第二个阶段是对梯度张量仪整体存在的误差进行校正。不同测量方法获得的磁梯度分量所存在的误差各不相同，难以统一表达。现有的技术大部分还停留在第一阶段，第二阶段的校正还没有什么比较简便的方法。技术实现要素：：本发明的目的就在于针对现有技术的不足，提供一种直接从第二阶段的磁梯度张量分量出发获得最优的校正参数的一种基于磁梯度不变量的磁梯度计校正方法。本发明的目的是通过以下技术方案实现的：首先对构建张量仪时所存在的标度因子误差、非正交误差、非对准误差、零偏误差进行建模。然后借鉴磁矢量仪校正时的标量约束法，利用磁梯度张量两个独立的旋转不变量进行约束，获得最优的校正参数。一种基于磁梯度不变量的磁梯度计校正方法，包括以下步骤：步骤一、在二维空间对张量仪误差进行建模；步骤二、由二维空间扩展到三维空间对张量仪误差进行建模；步骤三、建立校正补偿模型；步骤四、利用磁偶极子先进行旋转校正数据；步骤五、利用磁梯度不变量特性通过最小二乘法获取校正系数；步骤六、进行测线数据测量，将张量仪装配到飞行器上，让飞行器演设计好的测线进行飞行，张量仪采集测线上的磁场数据；步骤七、进行校正，利用步骤五中的求得的校正系数对测线上测量的数据进行校正，得到校正值。有益效果：本发明是直接从张量仪整体误差出发，对张量仪的误差进行建模，利用磁梯度张量两个独立的旋转不变量进行约束，获得最优的校正参数，更深入地对张量仪误差进行校正，使测量的数据更为可靠；相对于目前校正张量仪整体误差繁琐复杂的方法，本发明直接对测量数据结果进行处理，不需要提供其它的数据，更为简便，此外本发明不受限于各种磁梯度测量原理既可在有地磁场的野外环境下使用，也可在磁屏蔽环境中使用。附图说明：图1基于磁梯度不变量的磁梯度计校正方法流程图。图2二维空间中测量张量分量gxx和gyy时梯度计的理想情况。图3二维空间中测量张量分量gxx和gyy时张量仪存在非对准误差。图4二维空间中测量张量分量gxx时张量仪存在非正交误差的情况。图5三维空间中非正交误差示意图。图6测量值、校正值与理论值误差的rmse对比。图7测线ct测量值、校正值与理论值对比。具体实施方式：下面结合附图和实施例对本发明做进一步的详细说明：一种基于磁梯度不变量的磁梯度计校正方法，包括以下步骤：步骤一、在二维空间对张量仪误差进行建模；步骤二、由二维空间扩展到三维空间对张量仪误差进行建模；步骤三、建立校正补偿模型；步骤四、利用磁偶极子先进行旋转校正数据；步骤五、利用磁梯度不变量特性通过最小二乘法获取校正系数；步骤六、进行测线数据测量，将张量仪装配到飞行器上，让飞行器演设计好的测线进行飞行，张量仪采集测线上的磁场数据；步骤七、进行校正，利用步骤五中的求得的校正系数对测线上测量的数据进行校正，得到校正值。步骤一、在二维空间对张量仪误差进行建模实际的仪器制造和安装过程中存在在非正交误差与非对准误差。在二维空间中对两个理论上测量磁场x分量在x轴梯度gxx与磁场y分量在y轴方向上梯度gyy的梯度计进行分析，得到gxx分量测量值rxx与gyy分量测量值ryy的表示方式：先通过公式(1)和公式(2)分别计算矩阵nx与ny,然后取其中的nx11为rxx，ny22为ryy，其中，α为基线非对准角，γ为基线非正交角，β为梯度计所测磁场分量非对准角，θ为梯度计所测磁场分量非正交角。同理，二维空间中其他梯度的误差模型也可以通过类似方式表示。其中c*表示cos*，s*表示sin*。步骤二、由二维空间扩展到三维空间对张量仪误差进行建模，并且建立补偿校正模型假设rxx和ryy是gxx和gyy分量的测量值，其可通过公式(3)-(5)计算，分别取nx和ny中的nx11和ny22为rxxandryy。其中：αi,βi,γi和δi表示误差角。因此，每个测量的分量rμυ(μ,υ＝x,y,和z)只含有非正交与非对准误差，可以表示为：步骤三、可以建立校正补偿模型磁场沿x,y,z三个方向的二阶导数可构成磁梯度张量g，尽管g有九个分量，由于在不包括场源的域内，磁场的散度和旋度为0，即对称且迹为0，故只有五个分量是独立的，可表示为：而实际的测量值tμυ还含有标度因子误差c,和零偏误差o,可以表示为：tμυ＝cμυnμυ+oμυ.(7)因此只含有五个独立分量的张量测量值可以表示为：其中张量的校正模型可以写为:步骤四、利用磁偶极子先进行旋转校正数据获取在地面将仪器装配好，以磁偶极子作为磁源，让张量仪绕轴进行旋转，旋转要尽量覆盖到各个角度，张量仪采集不同姿态下带磁干扰的磁场测量数据。步骤五、利用磁梯度不变量特性通过最小二乘法获取校正系数不变量是指在张量进行坐标变换时其值可以通过一系列计算得到一个不变常数，张量具有两个非零独立不变量：i2＝|g|.(11)第一步是用不变量i1，进行校正：将公式(12)中的gμυ用公式(9)中的tμυ代入展开可以得到公式(12)其中x1-x15是hij的多项展开式，x16-x20由hij和dij组成。当磁张量梯度仪绕其中心旋转，它可以测量n组带误差的张量值。根据不变的性质，x1-x20应该保证fi(i＝1...n)不变.所以,我们设计公式(15)中的函数j利用最小二乘法计算出最佳的x1-x20。将(9),(10),和(12)联立可以得到二次型：(t-o)ta(t-o)＝1.(14)其中所以零偏误差o可以通过x1-x20来计算。将零偏误差消除之后，(9)和(10)可以修改为：同样的，y1-y15是hij组成的多项式可以通过最小二乘法进行计算。以系数y1为例进行展开有:所以,15个系数可以得到15个方程，将这15个方程联立可以得到方程组e1。由于方程个数小于未知量个数，因此还需要使用不变量i2进行校正。将(11)展开,我们得到了一个关于gμυ的多项式：将公式(18)中的用(15)中的t'代入可以得到公式(19)：其中，z1-z35是hij组成的多项式可以通过最小二乘法进行计算。因此35个等式可以组成方程组e2，将e1和e2联立通过matlab的数值计算可以解出方程组的解得到校正系数，最后我们可以通过公式(9)来进行校正。步骤六、进行测线数据测量将张量仪装配到飞行器上，让飞行器演设计好的测线进行飞行，张量仪采集测线上的磁场数据。步骤七、进行校正利用步骤五中的求得的校正系数对测线上测量的数据进行校正，得到校正值。本方法以单个磁梯度计为基础，由二维空间先对其构建张量仪时存在的非对准误差、非正交误差进行建模，再扩展到三维空间，在建模中加入标度因子误差、零偏误差建立校正补偿模型。现在地面进行旋转校正数据获取，利用磁梯度张量两个独立的旋转不变量进行约束，利用最小二乘法获得最优的校正参数，再将校正系数应用于测线数据校正，获取校正数据。以测量gxx，gxy，gxz，gyy和gyz分量的张量仪进行分析，提供一种张量仪的校正补偿方法。在具体应用实例中，可以通过仿真进行模拟。该方法通过以下步骤实现：步骤一、在二维空间对张量仪误差进行建模先在二维空间中分析非正交与非对准误差的情况，图2所示为测量磁场x分量在x轴方向与y分量y轴方向上的梯度(gxx,gyy)时,两个梯度计的摆放示意图，其中虚线箭头表示梯度计的感应方向。在制造和安装过程中存在非对准和非正交误差。图3示出了分别在基线和感应方向上具有非对准角度α和β的梯度计。原本应该测量gyy分量的梯度计实际上测量的是y'轴方向上的磁场分量y'的变化。y'的感应方向等同于y以角α和β为旋转角旋转两次的感测方向。此外，x″轴和y'轴之间的非正交角γ以及感应方向x″和y'之间的非正交角θ也在图4中给出，原本应该测量gxx分量的梯度计实际测量值为磁场分量x″在x”轴方向上的变化。二维空间中理论张量为：因此如果实际测量值gyy有图1中所示的误差，实际上y'的感应方向等同于y以角α和β为旋转角旋转两次，而y'轴相当于以角α旋转了一次。所以gyy测量值可以通过公式(2)计算，用ryy表示。ryy值为ny中的ny22：测量的分量gxx的梯度计的基线存在非正交角γ。由于基线中的非正交误差，感测方向已经以角度γ进行旋转。此外，在x”和y'的感测方向之间存在另一非正交角度θ。假设rxx是gxx的测量值，其可以经由(3)计算，rxx值为nx中的nx11。其中s*和c*表示正弦和余弦函数。二维空间中其他分量的表达方法与之类似。步骤二、由二维空间扩展到三维空间对张量仪误差进行建模，并且建立补偿校正模型我们以gxx和gyy分量为例推出三维空间对张量仪误差模型的表示。具体如下：⑴、假设在基线中存在非对准角α1,β1,和γ1，则梯度计可以被认为以这三个角为欧拉角绕轴旋转，变换矩阵可以由m定义。同样的在感应方向中若存在非对准角α2,β2,和γ2，则其变换矩阵可以由l定义。⑵、假设在基线中存在三个非正交角α3,β3,和γ3，新产生的坐标轴为x',y',和z。其中理论上的z轴与实际z轴是重合的；y'oz平面与yoz也是重合的，δ3是y'轴与y轴之间的角度；p是x'轴在xoy平面上的投影，其中α3是x'轴和p轴之间的夹角，β3是x轴和p轴之间的夹角。所以非正交变换矩阵可以由w3定义。同时感应方向受到了基线非正交的影响产生变化：x'相当于x方向分别绕z轴和y轴以β3角和α3角依次旋转两次得到，变换矩阵可以由w2定义；y'相当于y方向绕x轴以δ3角旋转得到，变换矩阵可以由w5定义。⑶、假设在感应方向中存在三个非正交角α4,β4,和γ4，其变换可以由相类似的方法推导，非正交矩阵由w1和w4定义。假设rxx和ryy是gxx和gyy分量的测量值，其可通过公式(4)-(5)计算，分别取nx和ny中的nx11和ny22为rxxandryy。其中：αi,βi,γi和δi表示误差角。因此，每个测量的分量rμυ(μ,υ＝x,y,和z)只含有非正交与非对准误差，可以表示为：步骤三、可以建立校正补偿模型磁场沿x,y,z三个方向的二阶导数可构成磁梯度张量g，尽管g有九个分量，由于在不包括场源的域内，磁场的散度和旋度为0，即对称且迹为0，故只有五个分量是独立的，可表示为：而实际的测量值tμυ还含有标度因子误差c,和零偏误差o,可以表示为：tμυ＝cμυnμυ+oμυ.(8)因此只含有五个独立分量的张量测量值可以表示为：其中张量的校正模型可以写为:其中包含了30个待求系数,h中有25个,写作hij,d中有5个写作dij.步骤四、利用磁偶极子先进行旋转校正数据获取在地面线将仪器装配好，以磁偶极子作为磁源，让张量仪绕轴进行旋转，旋转要尽量覆盖到各个角度，张量仪采集不同姿态下带磁干扰的磁场测量数据。在仿真中模拟有5个安装好的梯度计分别测量磁梯度张量中的五个独立的分量gxx,gxy,gxz,gyy,和gyz。在地面先进行旋转校正，再在低空的一条测线上用旋转校正得到的校正系数观测校正效果，具体的仿真有如下设定：①、仿真中的磁偶极子在某一位置形成的磁梯度张量可以由磁场强度、磁偏角、磁倾角以及其具体位置通过公式(11)计算。同样，在测线上计算每个采样点的梯度值便可以得到整条测线上的梯度曲线。其中，μ0是真空中磁导率，r是方向向量，m是磁偶极子磁矩，δij是克罗内克δ，i,j＝1,2,3表示笛卡尔坐标系下的x,y,z。②、给张量仪加入随机的旋转角，计算得到不同姿态下张量仪理论输出值，用于得到校正系数。③、张量仪的输出可以由各种误差由上述模型导出，具体的误差设置如表1所示。④、将磁矩矢量为(250,000,250,000,-353,553.39)a·m2的磁偶极子作为测量目标埋入地下5米，采集磁偶极子正上方距离地面10米高处的测线数据，测线长100米，测线上均匀设置了500个采样点，得到测线上的测量数据。表1仿真中张量仪误差设定标度因子误差在-0.01—0.01之间均匀分布轴间非正交误差在-1°—1°之间均匀分布轴间非对准误差在-3°—3°之间均匀分布感应非对准误差在-1°—1°之间均匀分布零偏在-15nt/m—15nt/m之间均匀分布噪声振幅为0.1nt/m的均匀分布噪声。步骤五、利用磁梯度不变量特性通过最小二乘法获取校正系数不变量是指在张量进行坐标变换时其值可以通过一系列计算得到一个不变常数，张量具有两个非零独立不变量：i2＝|g|.(13)第一步是用不变量i1，进行校正：将公式(12)中的gμυ用公式(10)中的tμυ代入展开可以得到公式(14)其中x1-x15是hij的多项展开式，x16-x20由hij和dij组成。当磁张量梯度仪绕其中心旋转，它可以测量n组带误差的张量值。根据不变的性质，x1-x20应该保证fi(i＝1...n)不变.所以,我们设计公式(15)中的函数j利用最小二乘法计算出最佳的x1-x20。将(10),(12),和(14)联立可以得到二次型：(t-o)ta(t-o)＝1.(16)其中所以零偏误差o可以通过x1-x20来计算。将零偏误差消除之后，公式(10)和公式(12)修改为：同样的，y1-y15是hij组成的多项式可以通过最小二乘法进行计算。以系数y1为例进行展开有:所以,15个系数可以得到15个方程，将这15个方程联立可以得到方程组e1。由于方程个数小于未知量个数，因此还需要使用不变量i2进行校正。将(13)展开,我们得到了一个关于gμυ的多项式：将公式(18)中的用(17)中的t'代入可以得到公式(21)：其中，z1-z35是hij组成的多项式可以通过最小二乘法进行计算。因此35个等式可以组成方程组e2，将e1和e2联立通过matlab的数值计算可以解出方程组的解得到校正系数，最后我们可以通过公式(10)来进行校正。步骤六、进行测线数据测量将张量仪装配到飞行器上，按表1中的设定仿真飞行器沿设计好的测线进行飞行，张量仪采集测线上的磁场数据。步骤七、进行校正利用步骤五中的求得的校正系数对测线上测量的数据进行校正，得到校正值。具体的校正效果如下：所有仿真系数根据表1生成，仿真重复1000次，均方根误差用来评估理论和未校正gxy和校正gxy之间的误差,1000次仿真中每一对均方根误差仿真结果如图6所示。其他分量校正结果结果如表2所示，校正的效果为38.58倍到60.83倍.表2五个分量1000次仿真中平均rmsesgxxgxygxzgyygyz校正前(nt/m)7.307.507.507.337.54校正后(nt/m)0.120.130.180.190.15改善幅度60.8357.7041.6738.5850.27图7展示了在某一次仿真中，在测区中间两条测线上理论ct与校正前后ct的对比结果，rmse在校正之后从17.78nt/m减小到0.09nt/m。五个分量校正结果类似于ct，具体如表3所示:五个分量校正结果类似于ct如表3所示.校正改善效果为30.15倍到99.89倍.表3一次仿真中五个分量的rmsegxxgxygxzgyygyz校正前(nt/m)5.003.929.776.988.99校正后(nt/m)0.080.130.250.140.09改善幅度62.5030.1539.0849.8699.89当前第1页12