一种基于预测值量测转换的状态融合目标跟踪方法与流程

本发明属于雷达目标跟踪领域，特别是涉及利用多普勒雷达量测转换误差的统计特性的计算方法。

背景技术：

目前，在目标跟踪系统中，目标的状态方程一般是建立在直角坐标系下的，而量测值一般是在极坐标系下获得的。这样，目标跟踪就成为一个非线性估计问题。解决这一问题的常用方法是转换量测卡尔曼滤波(cmkf)算法，即使用转换量测方法将极坐标下的量测变换表示成直角坐标系下的量测，从而使目标跟踪就成为一个线性估计问题。然而传统的转换量测的方法在转换量测时会产生偏差(见文献：lerro.d,andbar-shalom.y,trackingwithdebiasedconsistentconvertedmeasurementsversusekf,ieeetransactionsonaerospaceandelectronicsystems,29,3(july1993),1015-1022.)。如何去除转换量测值的偏差是提高雷达目标跟踪的精度的关键。已有不少学者对此问题进行了研究，提出了一些改进方法，如去偏的转换量测卡尔曼滤波(dcmkf)、无偏转换量测卡尔曼滤波(ucmkf)算法、修正的无偏转换量测卡尔曼滤波(mucmkf)算法以及基于预测位置的去相关无偏量测转换卡尔曼滤波(ducmkf)算法。

上述算法都仅仅考虑了雷达的位置量测。实际采用的雷达，尤其是多普勒雷达，除了获得位置量测信息，还有多普勒量测。理论计算与实践已经证明，充分利用多普勒量测信息可以有效地提高目标的跟踪精度。早先通常假设距离、角度和多普勒的量测误差统计独立。然而最近的研究表明，对于某些波形而言，斜距和多普勒的量测误差是统计相关的。为减小多普勒量测模型在直角坐标系下的强非线性，学者们通过将斜距和多普勒量测相乘构造了伪量测。段战胜，韩崇昭(见文献：zhanshengduan,chongzhaohanandx.rongli,sequentialnonlineartrackingfilterwithrange-ratemeasurementsinsphericalcoordinates,7thinternationalconferenceoninformationfusion,stockholm,2004,131-138.)将去偏量测转换算法推广为包含多普勒量测且斜距误差和多普勒误差相关的序贯滤波算法，然而，这篇文献中求解误差均值和协方差时使用了嵌套的条件期望，导致了偏差。文献(zhougongjian,pelletiermichel,kirubarajanthiagalingan,etal..staticallyfusedconvertedpositionanddopplermeasurementkalmanfilters[j].ieeetransactionsonaerospaceandelectronicsystems,2014,50(1):300-316.)提出了由位置量测转换卡尔曼滤波器估计目标位置状态，再由多普勒量测转换卡尔曼滤波器估计伪状态，最后利用前面两个状态估计结果基于最小均方误差准则下建立新的状态估计器，得到最终状态结果。但是该算法仅仅在量测值的条件下推导转换量测误差的均值和协方差矩阵，导致协方差矩阵和量测误差是相关的。这种相关性导致卡尔曼增益依赖于量测误差，进而状态估计是有偏差的。

技术实现要素：

为了更加充分地利用雷达的多普勒量测信息，本发明使用基于预测值量测转换方法计算转换量测误差的统计特性，以直角坐标系下的位置预测值为条件获得转换量测误差的均值和协方差，消除转换量测误差协方差和量测误差的相关性；然后，对位置和多普勒量测进行状态估计，最后使用最小均方误差准则融合位置和多普勒状态估计结果，得到最终的状态估计。该跟踪方法同时还可以扩展到3d雷达的cv和ca运动模型中。

本发明主要包括三部分：第一部分，基于预测值量测转换的位置状态估计；第二部分，基于预测值量测转换的多普勒伪状态估计；第三部分，使用最小均方误差准则融合位置状态估计和多普勒伪状态估计结果，进行递推卡尔曼滤波，实现目标跟踪；

因而本发明的技术方案为，一种基于量测转换卡尔曼滤波状态融合的目标跟踪方法，该方法包括：

运动目标位置状态方程和量测矩阵分别是

xp(k+1)＝fpxp(k)+γpv(k)

其中，fp为位置状态转换矩阵，γp为位置状态噪声输入矩阵，为位置去偏转换量测。hp为位置量测矩阵，系统状态噪声v(k)＝[vx(x)vy(x)]^t，其中vx(x)和vy(x)是位置状态在x和y方向的高斯过程噪声，其均值为零，协方差q(k)＝diag(q,q)；wp(k)是量测转换误差向量，其均值为零，相关矩阵为rp(k)；

运动目标多普勒伪状态方程和量测方程：

η(k+1)＝fηη(k)+gu(k)+γxvx(k)+γsvs(k)

其中，与位置状态向量xp(k)满足非线性关系vx(k)＝xγv(k)，xγ是位置状态在多普勒伪状态中的噪声输入矩阵分量；fη为多普勒伪状态转换矩阵，g、γx和γs是多普勒伪状态噪声输入矩阵；为去偏多普勒伪量测，hη是量测转换矩阵；wη(k)是零均值高斯白噪声，其协方差矩阵是rη(k)；

首先获取以下数据信息：雷达采样周期为t，获取的量测数据分别为距离量测rm、方位角量测αm和多普勒量测其量测噪声是零均值高斯白噪声，方差分别为和距离量测和多普勒量测噪声相关系数为ρ；在直角坐标系下，系统状态噪声v(k)＝[vxvy]^t，vx和vy是位置状态在x和y方向的高斯过程噪声，其均值为零，协方差矩阵为q(k)，假设目标运动模型为cv模型；

步骤1：滤波器初始化

利用前2个时刻，即k＝0,1时刻的量测值，计算k＝1时的位置状态估计值和其估计误差协方差pp(1)，多普勒伪状态估计值和其估计误差协方差pη(1)，位置状态和多普勒伪状态估计误差互协方差ppη(1)。

步骤2：位置状态估计滤波；

步骤2.1：将时刻极坐标系下的量测值rm(k)和αm(k)转换到直角坐标系下，得到位置量测xm(k)和ym(k)；xm(k)表示x轴坐标，ym(k)表示y轴坐标；

步骤2.2：根据如下公式对位置量测xm(k)和ym(k)去偏处理，得到无偏量测转换值

步骤2.3：根据如下公式计算位置状态的预测值；

其中，xt和yt为目标在直角坐标系下x轴和y轴方向位置状态预测值，和为目标的速度状态预测值；fp为k时刻的位置状态转移矩阵，为上一时刻位置状态估计结果；

步骤2.4：根据如下公式计算预测误差协方差矩阵；

pp(k+1,k)＝fppp(k,k)fp^t+γpq(k)γp^t

pp(k,k)为上一时刻的位置状态估计误差协方差，γp为状态噪声输入矩阵，q(k)为过程噪声相关矩阵；

步骤2.5：在预测值和预测误差协方差pp(k+1,k)条件下，根据如下公式计算极坐标系下预测距离rt及其预测误差方差

步骤2.6：在预测值和预测误差协方差pp(k+1,k)条件下，根据如下公式计算极坐标系下预测方位角αt及其预测误差方差

步骤2.7：在预测离rt和预测方位角αt及其预测误差方差条件下，根据如下公式计算位置去偏量测转换误差协方差rp(k+1)；

各元素详情如下：

rxy＝ryx

步骤2.8：根据如下公式计算位置状态滤波增益；

其中，hp为位置量测矩阵；

步骤2.9：根据如下公式计算位置状态估计；

其中，

步骤2.10：根据如下公式计算位置状态估计误差协方差；

pp(k+1,k+1)＝pp(k+1,k)-kp(k+1)hppp(k+1,k)

其中，

当计算出位置状态估计误差协方差后矩阵中各元素为已知值；

步骤3：多普勒伪状态估计滤波；

步骤3.1：根据如下公式由极坐标系下的距离量测rm(k)和多普勒量测构建多普勒伪量测ηm(k)；

步骤3.2：根据如下公式对多普勒伪量测ηm(k)去偏处理，得到无偏量测转换值

步骤3.3：根据如下公式计算位置状态的预测值

其中，fη为多普勒伪状态转移矩阵，η(k,k)为上一时刻多普勒伪状态估计结果，对于cv运动模型有

步骤3.4：根据如下公式计算多普勒伪状态预测误差协方差；

pη(k,k)为上一时刻的多普勒伪状态估计误差协方差。对于cv运动模型有qs(k)表示噪声矩阵vs(k)过程噪声相关矩阵，qx(k)表示噪声矩阵vx(k)的协方差矩阵，具体值如下所示；

qs(k)＝diag(2q²,2q²)

qs(k)表示噪声矩阵vs(k)过程噪声相关矩阵，qx(k)表示噪声矩阵vx(k)的协方差矩阵；和是该时刻位置状态估计矩阵的组成元素，和是该时刻位置状态估计误差协方差矩阵pp(k+1,k+1)的组成元素；

步骤3.5：在位置预测值和预测误差协方差pp(k+1,k)条件下，根据如下公式计算极坐标系下多普勒速度预测值及其预测误差方差

步骤3.6：在预测值和预测误差协方差pp(k+1,k)条件下，根据如下公式计算极坐标系下预测多普勒速度及其预测误差方差

步骤3.7：在预测距离rt和预测多普勒速度及其预测误差方差条件下，根据如下公式计算位置去偏量测转换误差协方差rη(k+1)；

rη(k+1)＝[rηη]

元素值如下：

步骤3.8：根据如下公式计算多普勒伪量测预测误差协方差；

sη(k+1)＝hηpη(k+1,k)hη^t+rηη(k+1)

其中，hη为多普勒伪量测矩阵；

步骤3.9：根据如下公式计算多普勒伪状态滤波增益；

步骤3.10：根据如下公式计算多普勒伪状态估计；

步骤3.11：根据如下公式计算多普勒伪状态估计误差协方差；

pη(k+1,k+1)＝pp(k+1,k)-pη(k+1,k)hη^tsη(k+1)^-1hηpη(k+1,k)^t

步骤4：融合位置状态估计和多普勒伪状态估计；

步骤4.1：在预测距离rt、预测方位角αt和预测多普勒速度及其预测误差方差条件下，根据如下公式计算位置量测和多普勒伪量测去偏量测转换误差互协方差rpη；

各元素值如下：

步骤4.2：根据如下公式计算位置状态和多普勒伪状态估计误差互协方差；

ppη(k+1,k+1)

＝[i-kphp]fpppη(k,k)fη^t[i-kηhη]^t

+[i-kphp]γpq(k)(γxxγ)^t[i-kηhη]^t+kprpη(k+1)kη

其中，i为np×nη维单位矩阵，其中np表示位置状态维数，nη表示多普勒伪状态维数，ppη(k,k)为上一时刻位置状态和多普勒伪状态估计误差互协方差，

步骤4.3：根据如下公式计算量测先验均值；

其中，ei表示第i个nη维直角坐标基向量，是近恒速度的jacobian矩阵，是hessian矩阵，其具体值如下；

pp表示步骤2.10的结果；

步骤4.4：根据如下公式计算先验状态和先验量测估计误差互协方差；

步骤4.5：根据如下公式计算先验量测估计误差协方差；

步骤4.6：根据如下公式计算最终状态估计结果；

步骤4.7：根据如下公式计算最终状态估计误差协方差；

p(k+1)＝pp-pxz(pzz)^-1pxz^t

步骤5：重复步骤2-4进行递推滤波算法，实现目标跟踪。

由于sf-ducm算法利用预测值处理量测转换误差协方差，克服了量测转换算法固有的缺陷。并且分别在位置状态、多普勒伪状态和状态融合3个步骤中进行滤波处理。因此，sf-ducm算法比一般可处理多普勒量测目标跟踪算法具有更高的跟踪精度。

附图说明

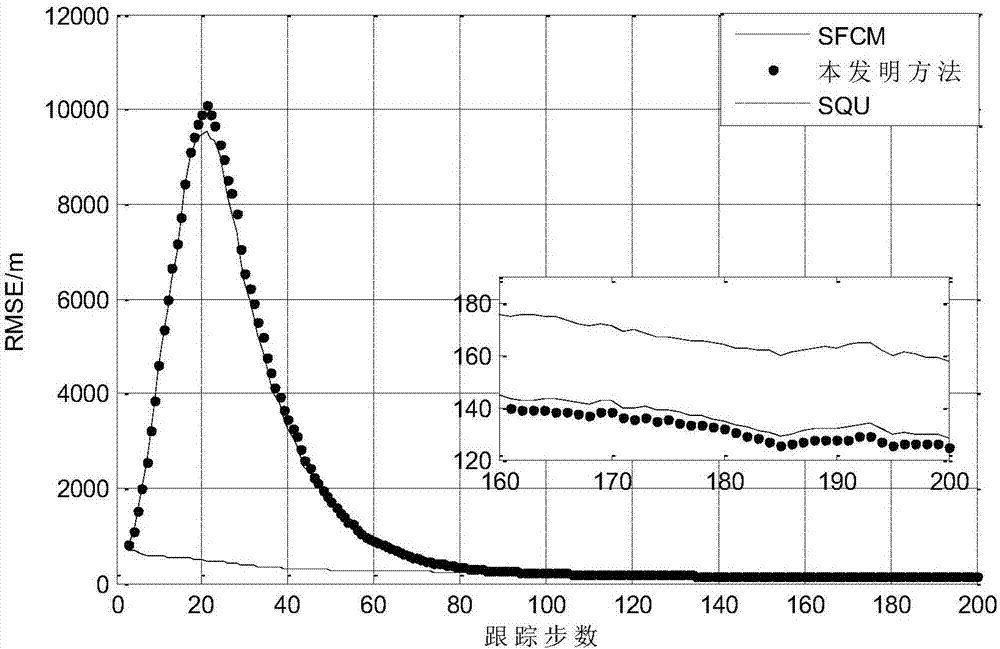
图1为具体实施方式中场景一与现有技术的仿真对比示意图；

图2为具体实施方式中场景二与现有技术的仿真对比示意图；

具体实施方式

在实施例中，考虑对极坐标2种目标运场景进行跟踪仿真。

在极坐标系下，传感器位于坐标原点，以采1s的采样周期提供目标的斜距、方位角和多普勒量测数据，量测过程噪声标准差0.001m²/s。目标初始值位置为(50km,50km)，初始速度为(5m/s,5m/s)。针对过程噪声标准差，距离、方位角、多普勒量测噪声标准差以及多普勒速度和距离的相关系数的不同取值，进行500次蒙特卡洛仿真。

场景一：传感器的距离量测误差为10m，方位角的量测误差为0.5度，多普勒速度的量测误差为0.1m/s，多普勒速度和距离的相关系数为0.1。

场景二：传感器的距离量测误差为30m，方位角的量测误差为0.7度，多普勒速度的量测误差为0.1m/s，多普勒速度和距离的相关系数为0.1。

图1和图2分别为本发明提出的算法对应具体实施方式中2种场景下和现有典型的基于量测值的融合量测转换(sfcm)滤波算法以及多普勒雷达序贯(squ)目标跟踪算法的匀速目标跟踪精度rmse仿真结果对比图。

通过对基于量测转换的跟踪算法分析，我们选取了基于量测值的融合量测转换(sfcm)滤波算法(见文献:zhougongjian,pelletiermichel,kirubarajanthiagalingan,etal..staticallyfusedconvertedpositionanddopplermeasurementkalmanfilters[j].ieeetransactionsonaerospaceandelectronicsystems,2014,50(1):300-316.)和序贯(squ)滤波算法(见文献：段战胜,韩崇昭.极坐标系中带多普勒量测的雷达目标跟踪.系统仿真学报,2004,16(12):2860-2863.)与本发明的基于ducm的静态融合量测(ducm-sf)滤波算法进行仿真比较。

所有算法在仿真过程使用了相同的目标初始状态及其估计误差协方差矩阵。目标跟踪性能指标为rmse值，定义如下：

其中和分别为第i次蒙特卡洛仿真时的x方向和y方向的状态估计的误差，n为蒙特卡洛次数。rmse的值越小，算法的跟踪精度越高。

从仿真结果可以看出，在两种情况下squ估计误差明显大于sfcm和sf-ducm的估计误差。这是由于squ算法将贯滤波估计结果反馈到下一时刻滤波器的输入，而sfcm算法采用静态滤波方法，没有把非线性滤波融合的结果反馈到下一时刻的滤波过程中，明显提高了估计精度。sf-ducm算法比基于量测值计算的sfcm算法估计误差小。这是由于sf-ducm算法利用预测值处理量测转换误差协方差，克服了量测转换算法固有的缺陷。综上所述，本发明算法改善了运动目标的跟踪性能，具有更好的效益。