输电铁塔主材角钢次弯矩的测量方法与流程

本发明涉及主材角钢次弯矩测量方法技术领域，尤其涉及一种输电铁塔主材角钢次弯矩的测量方法。

背景技术：

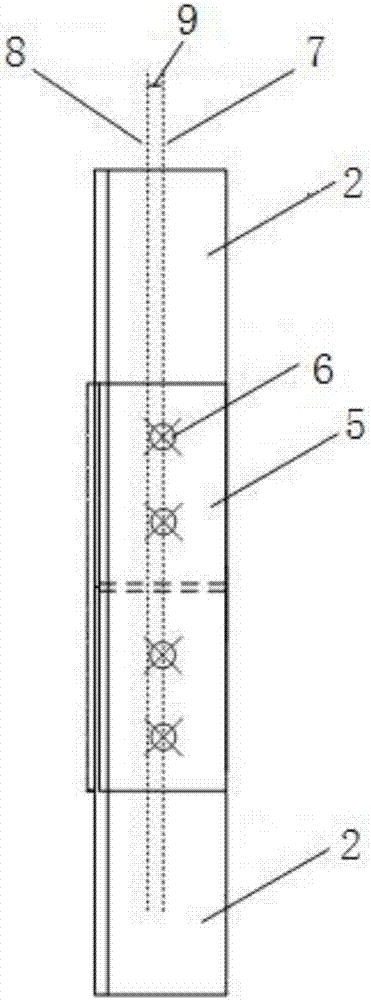
输电铁塔多是采用热轧等边角钢构件，通过螺栓连接而成的空间桁架结构。然而由于等边角钢是单轴对称构件，且包钢轴线与角钢轴线相互偏离(如图2所示)，从连接肢传递过来的力对截面的两个主惯性轴都有偏心，因而角钢构件将受到轴向载荷以及由于连接偏心产生的次弯矩的共同作用。为研究次弯矩对输电铁塔主材角钢的受力影响，必须计算出偏心受载时主材角钢的次弯矩大小。目前，尚未发现有测量输电铁塔主材角钢次弯矩大小的相关方法。

技术实现要素：

本发明所要解决的技术问题是提供一种简单、测量效率高的输电铁塔主材角钢次弯矩的测量方法。

为解决上述技术问题，本发明所采取的技术方案是：一种输电铁塔主材角钢次弯矩的测量方法，其特征在于包括如下步骤：

在输电铁塔主材角钢的两肢粘贴4个应变片，其中应变片a和应变片b粘贴在角钢主惯性轴与角钢两肢相交处，距离角钢顶点o'的距离均为m，应变片c和应变片d相对于角钢主惯性轴z轴对称布置，其距离角钢顶点o'的距离均为n；

采用半桥接线法将应变片a和应变片b接入应变仪，测量次弯矩mz产生的弯曲应变并根据应变及应力表达式计算次弯矩mz，其中mz是指所述主材角钢主惯性轴z轴的次弯矩；

采用半桥接线法分两次将应变片a和应变片b、应变片c和应变片d接入应变仪，测量次弯矩my产生的弯曲应变并根据应变及应力表达式计算次弯矩my，其中my是指所述主材角钢主惯性轴y轴的次弯矩。

进一步的技术方案在于：所述应变片a、应变片b、应变片c和应变片d的粘贴方向均沿角钢轴线方向。

进一步的技术方案在于：采用半桥接线法读取应变仪读数包括如下步骤：

将应变片a和应变片b作为相邻端接入应变仪，读取应变仪读数ε1；

将应变片a和应变片b作为相对端接入应变仪，读取应变仪读数ε2；

将应变片c和应变片d作为相对端接入应变仪，读取应变仪读数ε3。

进一步的技术方案在于：所述次弯矩mz的计算方法包括如下步骤：

分别求出测点a和b的应变表达式εa和εb；

对测点a和b的应变表达式联立求解，得出次弯矩mz产生的应变

结合应变仪读数ε1以及弯矩计算公式，计算次弯矩mz。

进一步的技术方案在于：所述次弯矩mz的计算方法包括如下步骤：

因主惯性轴y轴通过应变片a、b粘贴位置，次弯矩my将不会对应变片粘贴位置处应力产生影响，内力中只有轴力p和次弯矩mz影响该处应力的大小，应变均由拉伸和弯曲两种应变成分组成，即：

其中εp、分别表示由拉伸、弯曲所产生的拉应变、弯曲应变的绝对值；

对公式(1)和(2)联立求解，得出次弯矩mz产生的应变为；

将应变片b接入到应变仪ab段，将应变片a接入到应变仪bc段，则应变仪的读数为：

ε1＝εb-εa(4)

则

角钢构件在偏心的外载荷的作用下，其横截面上存在的内力分量有：轴力p，次弯矩my和次弯矩mz；根据叠加原理可知，偏心受力构件横截面上各点都为单向应力状态，其测点处正应力的理论计算公式为拉伸应力和弯矩正应力的代数和，即：

根据胡克定律可知，其测点处正应力的测量计算公式为材料的弹性模量e与测点处正应变的乘积，即：

σ＝e·ε(7)

根据公式(5)、(6)和(7)联立求解，计算出次弯矩mz为：

其中

则

进一步的技术方案在于：次弯矩my的求解包括如下步骤：

1)分别求出测点c和d的应变表达式εc和εd；

2)对测点a、b、c和d的应变表达式εa、εb、εc和εd联立求解，得出次弯矩my产生的应变

3)结合应变仪读数ε2和ε3以及弯矩计算公式，计算次弯矩my。

进一步的技术方案在于：次弯矩my的求解包括如下步骤：

内力中有轴力p、次弯矩my和次弯矩mz影响应变片c和应变片d处应力的大小，应变均由拉伸和弯曲两种应变成分组成，即：

其中εp表示轴向应力产生的轴向应变；表示次弯矩my产生的弯曲应变；表示次弯矩mz产生的弯曲应变；

由式(10)和(11)联立求解，得出次弯矩my产生的应变为：

由式(1)和(2)联立可得：

将应变片a接入到应变仪ab段，将应变片b接入到应变仪cd段，得应变仪的读数为：

ε2＝εa+εb(14)

则

将应变片c接入到应变仪ab段，将应变片d接入到应变仪cd段，得应变仪的读数为：

ε3＝εc+εd(16)

由式(12)、(15)和(16)联立得：

由公式(5)、(6)和(17)联立求解，计算出次弯矩my为：

其中

则

采用上述技术方案所产生的有益效果在于：所述方法基于应变片的粘贴位置以及应变片接入应变仪不同的接入方式，计算偏心受载时力对角钢截面两个主惯性轴的次弯矩大小，具有测量方法简单、实验效率高等优点，可有效应用于实际结构中偏心受载角钢的次弯矩测量，对输电铁塔的设计与校核有着重要影响。

附图说明

下面结合附图和具体实施方式对本发明作进一步详细的说明。

图1是本发明实施例所述方法中应变片的布片方式示意图；

图2是现有技术中角钢与包钢的连接示意图；

图3是本发明实施例所述方法中半桥接线法的示意图；

其中：1、形心2、输电铁塔主材角钢3、角钢主惯性轴y4、角钢主惯性轴z5、包钢6、螺栓孔7、角钢轴线8、包钢轴线9、偏心距。

具体实施方式

下面结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明的一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。

在下面的描述中阐述了很多具体细节以便于充分理解本发明，但是本发明还可以采用其他不同于在此描述的其它方式来实施，本领域技术人员可以在不违背本发明内涵的情况下做类似推广，因此本发明不受下面公开的具体实施例的限制。

如图1和图3所示，本发明实施例公开了一种输电铁塔主材角钢次弯矩的测量方法，包括如下步骤：

在输电铁塔主材角钢的两肢粘贴4个应变片，其中应变片a和应变片b粘贴在角钢主惯性轴与角钢两肢相交处，距离角钢顶点o'的距离均为m，应变片c和应变片d相对于角钢主惯性轴z轴对称布置，其距离角钢顶点o'的距离均为n；

采用半桥接线法将应变片a和应变片b接入应变仪，测量次弯矩mz产生的弯曲应变并根据应变及应力表达式计算次弯矩mz，其中mz是指所述主材角钢主惯性轴z轴的次弯矩；

采用半桥接线法分两次将应变片a和应变片b、应变片c和应变片d接入应变仪，测量次弯矩my产生的弯曲应变并根据应变及应力表达式计算次弯矩my，其中my是指所述主材角钢主惯性轴y轴的次弯矩。

具体的：

采用半桥接线法读取应变仪读数包括如下步骤：

将应变片a和b作为相邻端接入应变仪，读取应变仪读数ε1；

将应变片a和b作为相对端接入应变仪，读取应变仪读数ε2；

将应变片c和d作为相对端接入应变仪，读取应变仪读数ε3；

角钢构件在偏心的外载荷的作用下，其横截面上存在的内力分量有：轴力p，次弯矩my和次弯矩mz。

根据叠加原理可知，偏心受力构件横截面上各点都为单向应力状态，其测点处正应力的理论计算公式为拉伸应力和弯矩正应力的代数和，即：

根据胡克定律可知，其测点处正应力的测量计算公式为材料的弹性模量e与测点处正应变的乘积，即：

σ＝e·ε(2)

作为一种新的输电铁塔主材角钢次弯矩的测量方法，半桥接线法原理主要包括如下步骤：

下面结合图3对半桥接线法原理进行说明：

在进行测量时，有时只在电桥的ab段和bc段接应变片，而在ad和cd段连接应变仪内部的两个阻值相等的固定电阻。在此情况下，由于

r1＝r2＝rr3＝r4δr3＝δr4＝0(3)

所以，由式(3)可知，电桥的输出电压为

则应变仪的读数为

同理，若在电桥的ab段和cd段接应变片，而在ad和bc段连接应变仪内部的两个阻值相等的固定电阻，此时应变仪的读数为：

作为一种新的输电铁塔主材角钢次弯矩的测量方法，次弯矩mz的求解主要包括如下步骤：

在图1中a、b处粘贴应变片，且主惯性轴y轴通过应变片粘贴位置，因此次弯矩my将不会对应变片粘贴位置处应力产生影响，内力中只有轴力p和次弯矩mz影响该处应力的大小，应变均由拉伸和弯曲两种应变成分组成，即：

其中εp、分别表示由拉伸、弯曲所产生的拉应变、弯曲应变的绝对值。

对公式(7)和(8)联立求解，得出次弯矩mz产生的应变为；

如图3，将应变片b接入到ab段，将应变片a接入到bc段，则应变仪的读数为：

ε1＝εb-εa(10)

则

根据公式(1)、(2)和(11)联立求解，计算出次弯矩mz为：

其中

则

次弯矩my的求解流程主要包括如下步骤：

在图1中c、d处粘贴应变片，内力中则有轴力p、次弯矩my和次弯矩mz影响该处应力的大小，应变均由拉伸和弯曲两种应变成分组成，即：

其中εp代表轴向应力产生的轴向应变；代表次弯矩my产生的弯曲应变；代表次弯矩mz产生的弯曲应变；

由式(14)和(15)联立求解，得出次弯矩my产生的应变为：

由式(7)和(8)联立可得：

将应变片a接入到ab段，将应变片b接入到cd段，由式(6)得应变仪的读数为：

ε2＝εa+εb(18)

则

将应变片c接入到ab段，将应变片d接入到cd段，由式(6)得应变仪的读数为：

ε3＝εc+εd(20)

由式(16)、(19)和(20)联立得：

由公式(1)、(2)和(21)联立求解，计算出次弯矩my为：

其中

则

至此，通过4个应变片将偏心受载时输电铁塔主材角钢所受的次弯矩计算完毕。

所述方法基于应变片的粘贴位置以及应变片接入应变仪不同的接入方式，计算偏心受载时力对角钢截面两个主惯性轴的次弯矩大小，具有测量方法简单、实验效率高等优点，可有效应用于实际结构中偏心受载角钢的次弯矩测量，对输电铁塔的设计与校核有着重要影响。