基于GLMB滤波的多传感器TDOA无源定位方法与流程

本发明属于多传感器多目标跟踪领域，特别涉及一种基于多传感器平台的多目标定位跟踪方法。

背景技术：

无源定位系统完全被动地接收目标发射的电磁波进行定位和跟踪，具有隐蔽性好，生存能力强的特点，当只利用一对传感器到达时间差(简称tdoa)对目标进行无源定位时，目标的状态估计问题为非线性，且距离越远时估计越不乐观，这些特点决定了应该选用多对传感器对多目标进行跟踪定位，这也是本发明的现实依据。对于多个目标的定位需要进行预处理，主要是将不同目标的测量数据进行归并，使同一个目标的测量数据放在一起以备定位计算之用。预处理主要包括信号的分选和识别技术。由于观测数据不可避免的存在着环境噪声和测量误差，并且缺乏跟踪环境的先验知识，不能确定目标的数量，无法判定观测数据是由真实目标还是虚假产生，以及由哪一个真实目标产生。这些不确定因素破坏了观测与目标之间的对应关系，因此，多目标跟踪过程的关键是如何进行有效的数据关联。考虑到当目标个数达到一定数目时传统的数据关联算法会出现“组合爆炸”问题，本发明在随机有限集(简称rfs)框架下实现对多个目标的定位跟踪。

技术实现要素：

本发明针对现有技术的不足，提供了一种基于广义标签多伯努利(简称glmb)滤波的到达时间差(简称tdoa)无源定位跟踪方法。其具体内容如下：

一种多传感器平台的多目标无源定位方法，该方法包括以下步骤：

1.1系统建模；

状态方程：xk＝axk-1+bωk(1)

观测方程：

其中，xk＝{xk,1,xk,2,…,xk,n(k)}∈f(x)，表示多目标状态集合，n(k)＝|xk|表示k时刻存活的目标个数，xk,i是k时刻单个目标i的状态向量，p(k,i),x,p(k,i),y分别为k时刻目标i在直角坐标平面上的x轴和y轴上的坐标，分别为k时刻目标i在直角坐标平面上的x轴和y轴方向上的速度,a是目标状态转移矩阵,b是噪声矩阵.是系统量测，表示k时刻来自第q对传感器的量测，可能是来自于目标的量测，也有可能是来自杂波产生的虚警，αk表示k时刻目标的位置，u1,q,u2,q表示第q对传感器的位置，ωk,分别为过程噪声和量测噪声，服从标准的高斯分布。

1.2无源定位方法；

常用的传感器无源定位方法有到达时间差定位法、侧向定位法、到达时间定位法、多普勒频移定位法等。从定位精度、定位速度和抗干扰能力综合考虑，本发明采用到达时间差定位法(timedifferentofarrival,简称tdoa)，具体包括以下步骤：

假设在定位区域内每一时刻只有一个目标存在，则传感器对接收到的信号表示为：

y1(t)＝s(t)+v1(t)(3)

y2(t)＝s(t-τ)+v2(t)(4)

其中，s(t)是由信号源产生的信息，vi(t),i＝1,2是环境噪声，τ是两个传感器检测到的信号的时间差。用α∈r²表示信号源在笛卡尔坐标系下的位置，时间差τ的值取决于位置向量α，存在以下的非线性关系：

其中，||·||表示2范数，c表示声音的传播速度，u1和u2表示一对传感器在笛卡尔坐标系下的位置,tdoa估计的基本思想是寻找两路信号的最大相似性发生的时间差。在信号处理中，寻找二者之间的相似性通过广义互相关函数来估计得到，表示如下：

其中，rgcc(τ)是广义互相关函数，是tdoa的最大可能取值，是y1(t)和y2(t)的互谱密度，φ(ω)是权重函数，φ(ω)比较常用的一种选择是使用相位转移(phasetransform)，即

由于信号源的位置α随着时间的变化而改变，我们把对目标进行定位跟踪的时间段离散为若干个区间长度趋于零的区间，在每一个区间内认为α的值是几乎不变的，以此来估计时间差τ，用下式来估计互谱密度：

其中t表示时间戳的长度，k表示时间戳的下标。

用表示通过第q对传感器在第k个时间戳得到的tdoa。测量得到的tdoas表示为：

在这里，是时不变噪声，假设对于任意的q≠p，与是相互独立的，任意的服从均值为0，方差为的高斯分布。

2.glmb滤波

2.1多传感器多目标下的贝叶斯递推公式

在多目标定位领域中，面临的一个难点就是数据源的不确定性，即数据关联问题，数据关联首先产生于传感器观测过程和目标环境的不确定性，如检测目标的新生和死亡,传感器检测过程中对目标的漏检和虚警等。数据关联就是要解决哪个量测来自哪个目标的问题，常用的数据关联方法主要有多假跟踪、联合概率数据关联等。为了有效较为复杂的数据关联问题，mahler通过引入有限集统计(finitesetstatistics,简称fisst)理论，于1997年首次系统地在随机有限集(randomfiniteset,简称rfs)理论框架下将多传感器多目标跟踪问题描述为贝叶斯估计问题，并给出了相应的多目标贝叶斯滤波器的递推公式，为基于rfs的多目标跟踪方法提供了一个比较坚实的理论基础。本发明在此基础上实现对多目标的无源定位。

为了便于理解，本发明中使用的定义和一些数学符号的功能如下:表示f和g的内积。[h(·)]^x＝πx∈xh(x)为多目标的幂形式，按照约定，当x＝φ时该式等于1，并且x为向量或集合。多目标环境下的kronecker函数如下式所示：

目标是随着时间的推移来估计出状态xk。在连续贝叶斯框架下，假设知道在已知xk-1的前提下xk的概率密度函数，并表示为：

f(xk|xk-1)(12)

在给定xk的前提下的概率密度函数可表示为：

其中，(12)式为状态转移密度，(13)式为似然函数。用定义含序列的其中i＝1,…,k，q＝1,…,q.在贝叶斯框架下的后验概率密度函数表示为：

接着用一些最优准则来估计状态xk，比如最大似然法，最小二乘法和极大后验估计法等。后验概率密度函数遵循以下推导过程：

预测步：

更新步：

2.2标签rfs和glmb滤波

用单伯努利rfsx描述单个目标状态集，其概率密度为：

其中，r表示单个目标x存在的概率，p(x)为目标x概率密度。

多伯努利rfsx看作为由固定个数且相互独立的单伯努利rfsxⁱ的联合即各单伯努利存在概率为rⁱ，概率密度为pⁱ，对于有n个成员的随机有限集{x1,…,xn}，其多伯努利概率密度函数如下表示:

其中，并且相互独立，因此多伯努利rfs完全可由参数来描述。

在多目标跟踪中，使用多伯努利滤波器需要传感器检测时有较高的检测概率和较低的虚警率，而标签多伯努利(labeledmulti-bernoulli，简称lmb)滤波器并不受这些条件的约束。lmb滤波器可以利用标签rfs(labeledrfs)来估计目标轨迹，不同于传统的rfs，标签rfs(简称l-rfs)为不同目标状态x∈x添加了标签l∈l＝{αi:i∈n},其中n表示正整数集合,l为离散的标签空间，其元素都是唯一的，即αi≠αj(i≠j)。标签多伯努利密度函数如下式表示：

类似于多伯努利rfs,lmbrfs完全可以用来描述,其中ψ是索引集合，假设其组成部分是统计独立的。为了标记方便，假设映射α可以理解为一种身份映射，其组件索引对应于轨迹的标签。

下式是标签多伯努利密度的简化形式:

本发明使用扩展标签多伯努利(generalizedlabeledmulti-bernoulli,简称glmb)滤波算法估计目标的状态和个数，标准glmb滤波算法定义如下：

其中，c表示离散变量，p^(c)(·,l)表示概率密度，ω^(c)(i)为权重并且满足∑(i,c)∈f(l)×cω^(c)(i)＝1，f(l)为l上所有有限子集的集合。该标准glmb滤波算法在贝叶斯递推下封闭。

为了便于计算，将上述表达式变形为如下所示的表达式，称作δ-glmb：

其中，ω^(i,ξ)＝ω^(ξ)(i)，由于ω^(ξ)(j)＝∑i∈f(l)ω^(ξ)(i)δi(j)中求和的每一项中当且仅当i＝j时是非零项，故δ-glmb由glmb通过上式转化得到。

δ-glmb中初始时刻的多目标先验为：

每一个i∈f(l0)表示0时刻出生的目标的轨迹标签，表示此刻的权重，p0(·,l)是轨迹l表示的目标的动态状态的概率密度,l∈i)。

预测步：

其中，ωb(i+∩b)是新生标签i+∩b的权重，是存活标签i+∩l的权重。pb(·,l)是新生目标的概率密度，是由先验密度p^(ξ)(·,l)得到的存活目标的密度。f(·|·,l)表示存活目标的概率密度。

更新步：

其中，在一个固定的(i,ξ)中，θ^(m)＝{ζ⁽¹⁾,…,ζ^(m)}集合表示为在最大权重时的θ的m个元素，为截断后的归一划权重。

3.序贯蒙特卡洛方法实现

序贯蒙特卡洛(sequentialmontecarlo,简称smc)方法不受限于线性、高斯模型，它是通过从当前系统的状态分布中选取一系列带有权值的粒子来预测和更新下一时刻的系统状态，即处理目标的后验概率密度函数。如果采样的粒子数目足够多，对目标后验概率密度的估计就会很接近于真实值，可以用来表示粒子集，l表示粒子的个数，相应的权值为满足因此，可以用基于rfs的smc方法近似估计(15)和(16)式子中的贝叶斯递推过程，可以表示为：

其中，是集值版本的狄利克雷函数，k时刻的粒子集合可以由k-1时刻的粒子集合得到，可以表示为：

随着时间的推移，粒子的权值和状态将会随之改变，为了减小粒子退化现象带来的影响，需要对粒子进行重采样操作，并将(33)代入到(15)和(16)中，可以得到：

4.多传感器多目标似然函数

这一部分，介绍多传感器多目标似然函数g(z|x)，用表示多传感器多目标量测，多目标的所有信息都包含在多传感器后验概率密度函数之中，可以表示为：

其中，积分可以表示为：

多传感器多目标关联映射是一个函数l→s1×s2×…×sm，其中ss＝{0,1,…,|zs|}，如果则有i＝i′，表示的第l个元素，多传感器的关联映射集合θ是一个向量关联空间，其在域i里的子集表示为θ(i)，类似地，s＝1,…,m表示i＝i′，也意味着轨迹i在每次扫描中最多可以产生m个量测。

假设目标产生的量测和杂波产生的量测之间相互独立，则多传感器多目标似然函数可以表示为：

其中：

其中pd,m(x,l)表示传感器m的检测概率。

采用基于tdoa的方法来在rfs框架下建立多目标的观测模型，在获取目标量测以后，在多传感器多目标定位跟踪系统中选取了glmb滤波算法，从而实现对多目标状态和航迹定位跟踪。

本发明的有益效果：

本发明给出了一种静止传感器平台的多传感器多目标联合定位跟踪方法，通过多对传感器来获取跟踪区域内的多个目标的到达传感器对的时间差，在rfs框架下建立多目标的观测模型，在获取目标量测以后，作者在多传感器多目标定位跟踪系统中选取了glmb滤波算法，从而实现对多目标状态和航迹的定位跟踪。

附图说明

图1.仿真环境

图2.多目标的真实轨迹和估计的点迹

图3.多目标的个数估计

图4.多目标的最优次分配距离(ospa)

具体实施方式

以下结合附图对本发明作进一步说明。

本发明提供了一种静止传感器平台的多传感器多目标联合定位跟踪方法，其具体实施方式如下：

1)在[0,100]×[0,100]㎡的二维平面跟踪区域内，在固定位置放置三对传感器，对跟踪区域内做匀速直线运动的两个目标进行定位跟踪，三对传感器的位置分别为：(100m,95m)和(95m,100m),(5m,100m)和(0m,95m),以及(0m,5m)和(5m,0m)，目标1在k＝0s时出现，在k＝80s时消失于跟踪区域内，初始状态为x1＝[100m,-1m/s,0m,1m/s]^t,目标2在k＝20s时出现，在k＝100s时消失于跟踪区域内，初始状态为x2＝[90m,-1m/s,5m,1m/s]^t,如图1所示。

2)根据目标信号到达各传感器的时间差来获取目标的量测，在rfs框架下建立系统的观测模型，随后在多传感器多目标定位跟踪系统中选择glmb滤波算法，从而实现对多目标状态和航迹的定位跟踪。

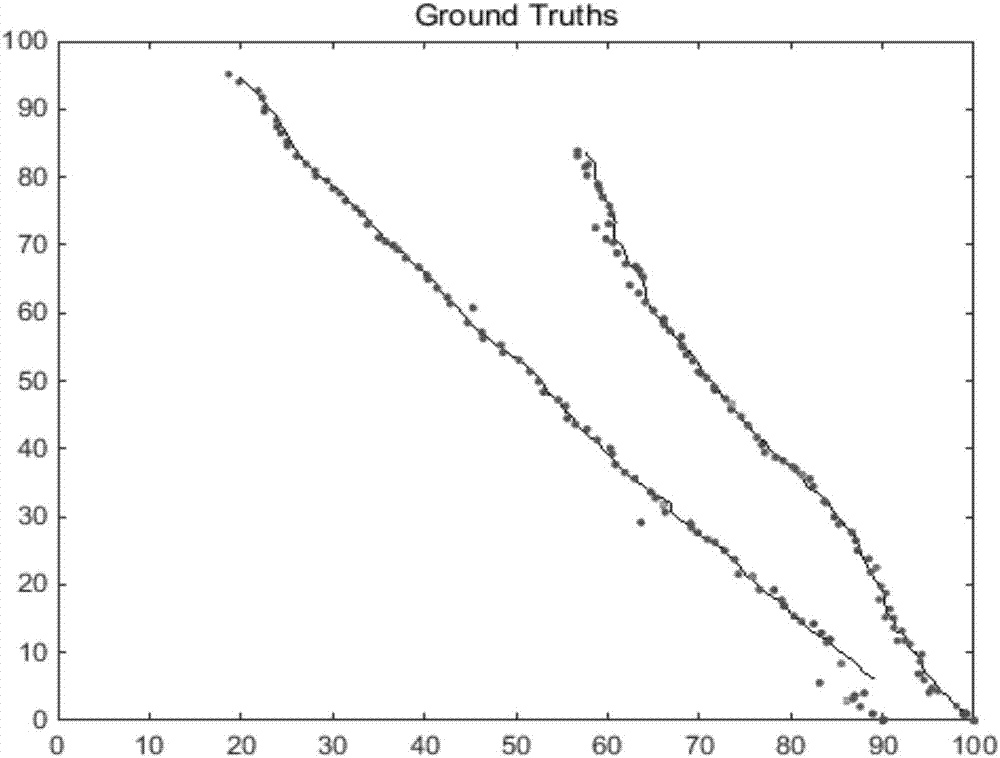
3)多目标的真实轨迹以及经过估计得到的点迹如图2所示，从图2可以看到，绝大部分的点都在真是轨迹上，或者很接近真是轨迹，定位跟踪效果比较好。

4)经过100次蒙特卡洛仿真得到的多目标个数估计结果如图3所示，从图3可以看出，跟踪得到的目标个数在比真实目标个数偏大一点点处上下做小幅度振动。由于虚警的存在，跟踪结果略微偏大。

5)为了综合评价本发明的性能，作者采用最优次分配距离来对目标的跟踪效果、目标个数估计以及综合性能进行评价，如图4所示，目标的跟踪效果比较好，目标的个数估计略微偏大，总体可以看出，本发明的综合性能比较好。

最后说明，以上描述仅用以说明本发明的技术方案而非限制其所包含范围，即对本发明的技术方案进行修改或者等同替换，而并未脱离其目的和范围的,均应涵盖于本发明的权利要求范围当中。