基于杂波协方差矩阵结构信息的自适应检测方法与流程

本发明涉及雷达技术领域，尤其涉及基于杂波协方差矩阵结构信息的自适应检测方法，在非均匀环境且训练样本数不足的情况下，能够利用结构信息减少对训练样本数量的需求进而提升检测性能。

背景技术：

近年来，随着雷达技术的日益成熟，雷达已被广泛用于军事预测、导弹制导、民航管制、地形测量、航海等众多领域。雷达的首先任务就是在噪声背景中检测出感兴趣的目标，只有具备了这样的功能，雷达才能给操作人员提供有效的目标方位、距离和运动轨迹等信息。

传统的雷达目标检测方法有：(1)reed，mallett和brennan于1974年提出的rmb算法：该方法首先利用训练样本数据得到协方差矩阵的极大似然(maximumlikelihood，ml)估计值，然后根据待检测信号的空间导向矢量来确定最优加权矢量，最后利用最优加权矢量以色噪声匹配滤波器的形式作用于待检测单元数据，将此滤波器的输出与合适的检测门限进行比较，从而判断待检测单元中有无目标信号。如果想要信噪比(signal-to-noiseratio，snr)损失不超过3db，那么大约需要两倍于数据维数的训练样本，该方法为后续自适应检测算法的发展奠定了理论基础。(2)kelly提出的基于均匀噪声环境的广义似然比检验(generalizedlikelihoodratiotest，glrt)原理的自适应检测算法：该检测方法通过将似然比在未知参量空间中寻找最大值，即用未知参数的ml估计值来代替似然比中的未知参数，从而得到检测统计量。(3)robey于1992年利用两步设计法提出的自适应匹配滤波器(adaptivematchedfilter，amf)：其核心思想是在第一步中假设噪声协方差矩阵已知，利用glrt原理得到针对其余未知参数的glrt统计检测量；在第二步中利用辅助数据得到噪声协方差矩阵的估计值，然后将这个估计值替换第一步所得检测统计量中的噪声协方差矩阵。

上述传统检测算法存在性能损失，且所需的训练样本数量较大。为此，有人提出了基于噪声协方差中央轭米对称性的检测算法，此类算法利用一个酉矩阵将杂波协方差矩阵由复数域转换到实数域，使待估计参数减少了一半，因此可将估计杂波协方差矩阵所需的训练样本数目减少了一半。即便是这样，在训练样本有限的情况下，现有的此类检测算法所需的训练样本数量仍较大，若训练样本数量不足则性能损失较为严重。

技术实现要素：

有鉴于此，本发明提供基于杂波协方差矩阵结构信息的自适应检测方法，能够进一步减少训练样本数量，并提升检测性能。

为达到上述目的，本发明采用如下技术方案：

提供一种基于杂波协方差矩阵结构信息的自适应检测方法，包括以下步骤：

步骤1，获取雷达系统全部n1个接收通道中每个接收通道在1个相干脉冲处理间隔内接收到的回波数据，得到n2个慢时间维采样点和l个快时间维采样点，n1≥1，n2≥1，l≥1；每个距离单元处采样数据的维数是n1×n2，排成一个长度为n的列向量，n＝n1×n2；所有采样数据形成n×l维的接收信号矩阵；其中，雷达系统静止不动，以等间隔发射相干脉冲串，且具有对称分布的线性阵列；接收信号矩阵包括地杂波信号，或，地杂波信号和目标信号；

步骤2，对待检测距离单元序号i进行初始化；

步骤3，将n×l维的接收信号矩阵的第i列数据确定为第i个待检测距离单元的信号，记为xi；选取第i个待检测距离单元附近k个距离单元的数据作为第i个待检测距离单元的k个训练样本，记为yk，k＝1，2，...，k，k≥1；

步骤4，对于第i个待检测距离单元的k个训练样本中的任一训练样本，构造与其对应的第一辅助信号和第二辅助信号，得到k个第一辅助信号和k个第二辅助信号，并提取k个第一辅助信号及k个第二辅助信号的实部和虚部；其中，与k个训练样本中的第k个训练样本yk对应的第一辅助信号为：第二辅助信号为：k取1到k之间的所有整数，j表示转置矩阵，*表示共轭操作；

利用k个第一辅助信号及k个第二辅助信号的实部和虚部，估算第i个待检测距离单元的杂波协方差估计矩阵其中，r1k表示第k个训练样本对应的第一辅助信号的实部，r2k表示第k个训练样本对应的第一辅助信号的虚部，r3k表示第k个训练样本对应的第二辅助信号的实部，r4k表示第k个训练样本对应的第二辅助信号的虚部，上标t表示转置操作；

步骤5，利用第i个待检测距离单元的杂波协方差估计矩阵及第i个待检测距离单元的信号xi，计算得第i检测统计量其中，p表示导向矢量，上标-1表示求逆操作，|·|表示取模值操作，上标h表示共轭转置转置操作；

步骤6，确定第i个待检测距离单元对应的检测门限λi；

将第i检测统计量ti与检测门限入进行比较：如果ti＞λi，则确定第i个待检测距离单元内有目标；如果ti≤λi，则确定第i个待检测距离单元内无目标；

步骤7，令待检测距离单元序号i加1，重复执行步骤3至步骤6，直至完成对所有待检测距离单元的检测。

现有的检测算法利用一个酉矩阵将杂波协方差矩阵由复数域转换到实数域，使待估计参数减少了一半，从而将估计杂波协方差矩阵所需的训练样本数目减少了一半。然而，在训练样本有限的情况下，现有的此类检测算法所需的训练样本数量仍较大，若训练样本数量不足则性能损失较为严重。而本发明方案利用雷达系统在静止不动且具有对称分布的线性阵列并以等间隔发射相干脉冲串的情形下，对应的杂波协方差矩阵具有中央轭米对称性这一特性，构造出二倍于原训练样本的数据，进一步的，由于杂波功率谱密度具有关于零频对称的特性，因此杂波协方差矩阵为一实矩阵，利用这一特性进一步将每一组数据中的实部和虚部提取出来，如此即可将训练样本数据扩展为原数据的四倍。换言之，在传统的处理方法中，若要求信噪比损失不超过3db，则大约需要两倍于数据维数的训练样本数据，最少需要等于数据维数的训练样本，而本发明方法所需的最少训练样本减少为数据维数的1/4。即，本发明方法能够减少对原训练样本的需求，并能有效提升检测性能。因此，即使是在训练样本有限的情况下，本发明方法也能进行有效检测。

附图说明

为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例或现有技术描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其他的附图。

图1为本发明实施例提供的一种基于杂波协方差矩阵结构信息的自适应检测方法的流程示意图；

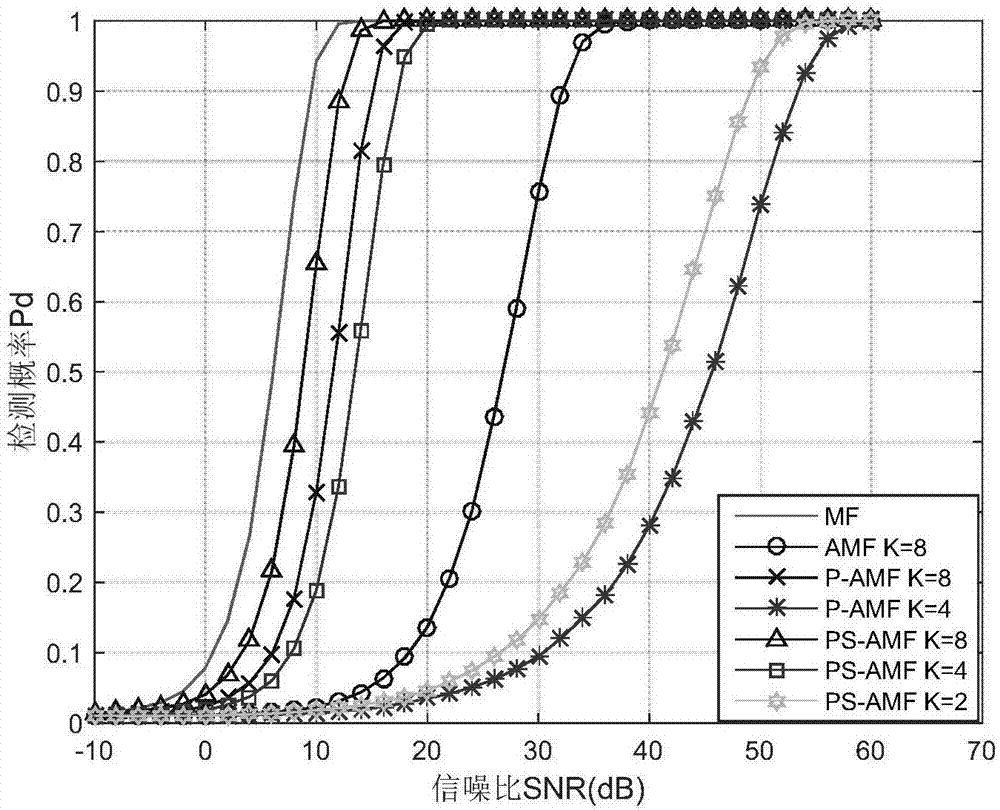
图2为匹配滤波方法、自适应匹配滤波方法、基于噪声协方差矩阵中央轭米对称性的检测方法以及本发明方法的检测概率随信噪比变化曲线图；

图3为匹配滤波方法、自适应匹配滤波方法、基于噪声协方差矩阵中央轭米对称性的检测方法以及本发明方法的检测概率随虚警概率变化曲线图。

具体实施方式

下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。

实施例一、

本发明实施例提供一种基于杂波协方差矩阵结构信息的自适应检测方法，如图1所示，该方法包括以下步骤：

步骤1，获取雷达系统全部n1个接收通道中每个接收通道在1个相干脉冲处理间隔内接收到的回波数据，得到n2个慢时间维采样点和l个快时间维采样点，n1≥1，n2≥1，l≥1；每个距离单元处采样数据的维数是n1×n2，排成一个长度为n的列向量，n＝n1×n2；所有采样数据形成n×l维的接收信号矩阵。

其中，雷达系统静止不动，以等间隔发射相干脉冲串，且具有对称分布的线性阵列；接收信号矩阵包括地杂波信号，或，地杂波信号和目标信号。

步骤2，对待检测距离单元序号i进行初始化。

步骤3，将n×l维的接收信号矩阵的第i列数据确定为第i个待检测距离单元的信号，记为xi；选取第i个待检测距离单元附近k个距离单元的数据作为第i个待检测距离单元的k个训练样本，记为yk，k＝1，2，...，k，k≥1。

步骤4，对于第i个待检测距离单元的k个训练样本中的任一训练样本，构造与其对应的第一辅助信号和第二辅助信号，得到k个第一辅助信号和k个第二辅助信号，并提取k个第一辅助信号及k个第二辅助信号的实部和虚部；利用k个第一辅助信号及k个第二辅助信号的实部和虚部，估算第i检测单元的杂波协方差估计矩阵

其中，与k个训练样本中的第k个训练样本yk对应的第一辅助信号为：第二辅助信号为：k取1到k之间的所有整数，j表示转置矩阵，*表示共轭操作。

第i个待检测距离单元的杂波协方差估计矩阵的表达式为：

其中，r1k表示第k个训练样本对应的第一辅助信号的实部，r2k表示第k个训练样本对应的第一辅助信号的虚部，r3k表示第k个训练样本对应的第二辅助信号的实部，r4k表示第k个训练样本对应的第二辅助信号的虚部。

以下给出上述步骤4的理论依据如下：

将目标检测问题用下面所示的二元假设检验来描述：

其中，h0表示无目标时的情况，雷达只收到杂波信号；h1表示有目标时的情况，雷达收到杂波信号加目标信号；式中，x表示待检测距离单元信号，xk表示与待检测距离单元信号独立同分布的一组训练样本，用来估计待检测距离单元的杂波协方差估计矩阵；p是已知的n×1维的信号导向矢量，α是确定的未知标量，由目标信号反射并受通道传播的影响，αp为目标信号表达式；噪声c是n×1列向量，其服从均值为零，方差为m的正则复高斯分布，m是n×n维的未知正定协方差矩阵，e[(xkxk^t)]＝0。

其中，复高斯向量x又可表示为：

x＝x1+jx2，

式中，x1＝real(x)，x2＝imag(x)，real(x)表示复向量x的实部，imag(x)表示复向量x的虚部。

当x服从正则复高斯形式时，有：

则，杂波协方差矩阵可以表示为：

进一步的，由于地杂波的功率谱密度函数是关于零频对称实偶函数，因此根据维纳-辛钦定理(宽平稳随机过程的功率谱密度是其自相关函数的傅里叶变换)，地杂波协方差矩阵是实偶的，也即这样就有：

进而有：

即杂波的实部和虚部协方差矩阵分别为m/2。

在本发明实施例中，由于雷达系统具有对称分布的线性阵列，且等间隔发射相干脉冲串，因此杂波协方差矩阵m具有中央轭米对称结构，它有双倍的对称性，即关于主对角线共轭对称以及关于副对角线对称，m满足：m＝jm^*j。其中，右上角标*表示取共轭，j是一个转置矩阵，

这样一来，利用杂波协方差矩阵的中央轭米对称结构，当xk～cn(0，m)时，则下式成立：

同时，又有类似于前述的推导过程，和的实部、虚部的协方差矩阵即为m/4。

基于这一结论，对于每个训练样本，即可构造对应的第一辅助信号和第二辅助信号并分别提取实部和虚部，得到4组数据，进而利用这4组数据估算待检测距离单元的杂波协方差矩阵。

步骤5，利用第i个待检测距离单元的杂波协方差估计矩阵及第i个待检测距离单元的信号xi，计算得第i检测统计量

其中，p表示导向矢量，上标-1表示求逆操作，|·|表示取模值操作，上标h表示共轭转置转置操作。

步骤6，确定第i个待检测距离单元对应的检测门限λi，将第i检测统计量ti与检测门限λi进行比较：如果ti＞λi，则确定第i个待检测距离单元内有目标；如果ti≤λi，则确定第i个待检测距离单元内无目标。

具体的，步骤6中，确定第i个待检测距离单元对应的检测门限入，具体可以包括：

获取雷达系统接收到的杂波数据，根据杂波数据利用蒙特卡洛方法，确定第i个待检测距离单元对应的检测门限λi。

其中，蒙特卡洛方法为本领域技术人员所熟知的技术手段，具体可参考《统计信号处理基础——估计与检测理论》(stevenm.kay著)的第一卷“估计理论”第七章“最大似然估计”的附录7a，本发明实施例对此不作介绍。

步骤7，令迭代次数i加1，重复执行步骤3至步骤6，直至完成对所有待检测距离单元的检测。

至此，本发明实施例提供的基于杂波协方差矩阵结构信息的自适应检测方法即结束。

现有的检测算法利用一个酉矩阵将杂波协方差估计矩阵由复数域转换到实数域，使待估计参数减少了一半，从而将估计杂波协方差估计矩阵所需的训练样本数目减少了一半。然而，在训练样本有限的情况下，现有的此类检测算法所需的训练样本数量仍较大，若训练样本数量不足则性能损失较为严重。而本发明方案利用雷达系统在静止不动且具有对称分布的线性阵列并以等间隔发射相干脉冲串的情形下，对应的杂波协方差估计矩阵具有中央轭米对称性这一特性，构造出二倍于原训练样本的数据，进一步的，由于杂波功率谱密度具有关于零频对称的特性，因此杂波协方差估计矩阵为一实矩阵，利用这一特性进一步将每一组数据中的实部和虚部提取出来，如此即可将训练样本数据扩展为原数据的四倍。换言之，在传统的处理方法中，若要求信噪比损失不超过3db，则大约需要两倍于数据维数的训练样本数据，最少需要等于数据维数的训练样本，而本发明方法所需的最少训练样本减少为数据维数的1/4。即，本发明方法能够减少对原训练样本的需求，并能有效提升检测性能。因此，即使是在训练样本有限的情况下，本发明方法也能进行有效检测。

以下通过仿真实验对本发明的上述有益效果进行验证说明：

1、仿真参数设置

将雷达系统的接收通道数设置为8，信噪比的取值范围设置为-10db至60db，信噪比的取值间隔设置为2db。

2.仿真内容

实验一：

将虚警概率固定设置为10^-2，分别采用匹配滤波方法(协方差矩阵已知)、自适应匹配滤波方法、现有的基于噪声协方差矩阵中央轭米对称性的检测方法以及本发明方法在不同的训练样本个数下进行10⁴次实验，统计不同的信噪比取值下的检测概率，并绘制检测概率随信噪比变化的曲线图。

实验结果如图2所示，图中横坐标为信噪比(单位为db)，纵坐标为检测概率，图例中“mf”表示匹配滤波方法，“amf”表示自适应匹配滤波方法，“p-amf”表示现有的基于噪声协方差矩阵中央轭米对称性的检测方法，“ps-amf”表示本发明方法，“k”表示训练样本个数。

实验二：

将信噪比固定设置为10db，分别采用匹配滤波方法(协方差矩阵已知)、自适应匹配滤波方法、现有的基于噪声协方差矩阵中央轭米对称性的检测方法以及本发明方法在训练样本个数为4时进行10⁴次实验，统计不同的虚警概率下的检测概率，并绘制检测概率随虚警概率变化的曲线图。

实验结果如图3所示，图中横坐标为虚警概率，纵坐标为检测概率，图例中“mf”表示匹配滤波方法，“amf”表示自适应匹配滤波方法，“p-amf”表示现有的基于噪声协方差矩阵中央轭米对称性的检测方法，“ps-amf”表示本发明方法。

3、仿真结果分析

从图2可以看出，本发明方法的检测概率高于现有的自适应匹配滤波方法以及基于噪声协方差矩阵中央轭米对称性的检测方法，并十分接近协方差矩阵已知的匹配滤波方法的检测概率。进一步来说，从图2可以看出，当检测概率为0.5、训练样本数量k＝8时，与匹配滤波方法的检测性能相比，本发明方法的检测性能损失约为3db，而现有的基于噪声协方差矩阵中央轭米对称性的检测方法和自适应匹配滤波方法的性能损失分别约为7db、21db，可以看出，同等条件下本发明方法的性能损失最小。

进一步的，从图3可以直观地看出，在相同的虚警概率下，本发明方法的检测概率明显高于现有的自适应匹配滤波方法以及基于噪声协方差矩阵中央轭米对称性的检测方法。

本领域普通技术人员可以理解：实现上述方法实施例的全部或部分步骤可以通过程序指令相关的硬件来完成，前述的程序可以存储于一计算机可读取存储介质中，该程序在执行时，执行包括上述方法实施例的步骤；而前述的存储介质包括：rom、ram、磁碟或者光盘等各种可以存储程序代码的介质。

以上所述，仅为本发明的具体实施方式，但本发明的保护范围并不局限于此，任何熟悉本技术领域的技术人员在本发明揭露的技术范围内，可轻易想到变化或替换，都应涵盖在本发明的保护范围之内。因此，本发明的保护范围应以所述权利要求的保护范围为准。