振型加权模态柔度的梁结构损伤识别方法与流程

本发明属于结构健康监测领域，具体涉及一种振型加权模态柔度的梁结构损伤识别方法。

背景技术：

桥梁结构大量地应用在高速公路、高速铁路等对国家经济发展具有重要作用的土木工程领域，是交通咽喉、国家经济发展的生命线工程，其健康状况日趋为民众所关注。目前，很多国家已在新建的重要桥梁结构上安装了健康监测系统，如香港青马大桥、苏通大桥、润杨长江公路大桥、日本明石海峡大桥等。如何对采集的大量数据进行分析，判断结构的状态是国内外的研究热点。

结构损伤识别是桥梁结构健康监测系统的重要组成部分，损伤检测一般至少包括三个方面：(1)判断结构是否存在损伤；(2)结构可能的损伤位置；(3)结构的损伤程度。由于损伤引起结构刚度的下降，进而引起结构模态参数的改变，故可通过模态参数进行结构损伤识别，如频率法、振型曲率法、柔度曲率法等。通过频率变化能够判别结构是否发生损伤，但由于频率是结构的整体参数，故不能有效地进行损伤定位。振型与结构的位置信息有关，因而可以进行损伤定位，但存在对曲率模态节点处损伤不敏感和不能有效反应损伤程度的问题，由于振型曲率法没有用到频率信息，因而其效果一般没有综合利用振型与频率的损伤识别方法效果好，如改进的曲率模态法、柔度曲率法等。

因结构柔度矩阵可以比较精确地由低阶模态建立，并且对损伤的敏感程度高于频率和振型，故其成为结构损伤识别中一类重要方法。早期的柔度损伤指标，采用模态柔度差以极大值的方式定位损伤，效果不理想，之后研究主要集中在柔度曲率类损伤指标，如均匀荷载面曲率差指标；使用柔度曲率矩阵列向量最大值、主对角线元素建立柔度矩阵曲率指标；对柔度矩阵差的行、列进行两次差分，以其列绝对最大值或对角元素作为检测结构损伤指标的方法等。

尽管现已对柔度类指标开展了较多的研究工作，但主要都集中在损伤定位方面，已有指标均不能有效地进行损伤程度识别。

技术实现要素：

本发明的目的在于针对现有模态柔度曲率损伤指标损伤定位的不足，以及不能进行损伤程度识别的问题，提供一种振型加权模态柔度的梁结构损伤识别方法。

本发明的振型加权模态柔度的梁结构损伤识别方法，包括如下步骤：

(1)通过模态测试分别获得梁结构损伤前、后的频率和振型；

(2)由损伤前、后的频率和振型计算振型曲率符号函数加权损伤指标，进行结构损伤定位；

(3)根据损伤前、后振型曲率符号函数加权损伤指标的相对变化计算梁结构节点损伤程度，进而计算得到单元损伤程度。

具体的，步骤(1)中，梁结构损伤前、后模态测试各跨的测点数目不少于8个，并且损伤前、后测点位置布置相同。

具体的，步骤(1)中，测试获得的模态阶数不少于3阶。

具体的，步骤(1)中，模态测试采用可测激励的方法，直接测得关于质量矩阵归一化的振型，或者采用仅测量输出的方法并通过梁结构的有限元模型建立质量矩阵，将振型对质量矩阵归一化。

具体的，步骤(2)中，梁结构振型曲率符号函数加权损伤定位指标mfcad计算公式如下：

其中，m为振型阶数，φi＝[φi1φi2lφin]^t为第i阶振型向量，n为测点数目，φi"表示第i阶振型的曲率，ωi为第i阶圆频率，j为测点号，δl为测点j-1到测点j的间距与测点j到测点j+1间距的平均值，下标u、d分别表示未损伤状态和损伤状态，ψu、ψd分别表示梁结构损伤前、后的振型曲率符号函数加权柔度矩阵，ψ＝[ψ(1)ψ(2)lψ(n)]^t。

具体的，步骤(3)中，节点损伤程度对静定结构采用如下公式计算：

节点损伤程度对于超静定结构，则采用如下公式计算：

其中，ψu(x)、ψd(x)分别表示梁结构损伤前、后x位置的振型曲率符号函数加权柔度矩阵值。

具体的，步骤(3)中，计算得到的节点损伤程度小于0的值置为0。

具体的，步骤(3)中，单元损伤程度采用如下公式计算：

其中，de(x)为x位置单元损伤程度，dn(x)为x位置节点损伤程度。

本发明基于结构损伤前后指标的相对变化及节点损伤程度与单元损伤程度的关系，提出了静定结构(如简支梁)和超静定结构(如连续梁)下相应指标损伤程度的计算方法。该方法能有效的对梁结构进行单损伤、多损伤工况的损伤定位，以及较精确的识别损伤程度，为梁结构无损检测与评估提供了一种有效的新方法。

附图说明

图1是本发明方法的流程框图。

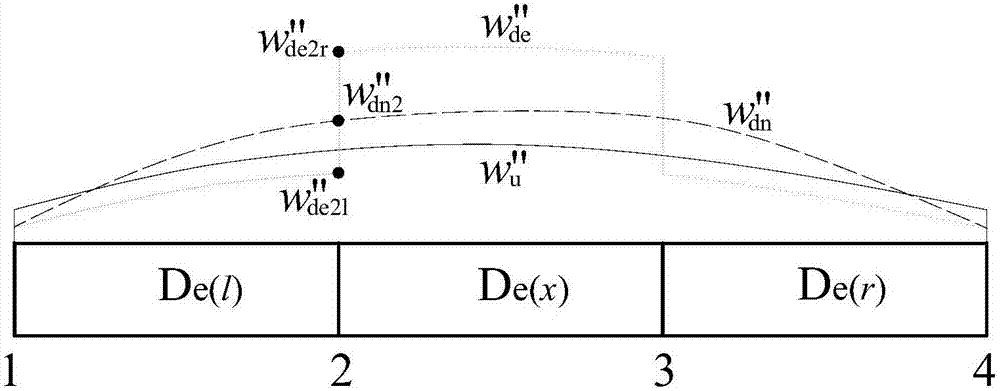
图2是本发明单元损伤与节点损伤关系图。

图3是本发明实施例一中简支梁有限元模型图。

图4是本发明实施例一中工况1mfcad指标损伤定位图。

图5是本发明实施例一中工况2mfcad指标损伤定位图。

图6是本发明实施例一中工况1mfcad指标损伤程度识别图。

图7是本发明实施例一中工况2mfcad指标损伤程度识别图。

图8是本发明实施例二中三跨连续梁有限元模型图。

图9是本发明实施例二中工况3c3指标损伤定位图。

图10是本发明实施例二中工况3ulsc指标损伤定位图。

图11是本发明实施例二中工况3mfcd指标损伤定位图。

图12是本发明实施例二中工况3mfccsm指标损伤定位图。

图13是本发明实施例二中工况3mfccd指标损伤定位图。

图14是本发明实施例二中工况3mfcad指标损伤定位图。

图15是本发明实施例二中工况4c3指标损伤定位图。

图16是本发明实施例二中工况4ulsc指标损伤定位图。

图17是本发明实施例二中工况4mfcd指标损伤定位图。

图18是本发明实施例二中工况4mfccsm指标损伤定位图。

图19是本发明实施例二中工况4mfccd指标损伤定位图。

图20是本发明实施例二中工况4mfcad指标损伤定位图。

图21是本发明实施例二中工况3c3指标损伤程度识别图。

图22是本发明实施例二中工况3ulsc指标损伤程度识别图。

图23是本发明实施例二中工况3mfcd指标损伤程度识别图。

图24是本发明实施例二中工况3mfccsm指标损伤程度识别图。

图25是本发明实施例二中工况3mfccd指标损伤程度识别图。

图26是本发明实施例二中工况3mfcad指标损伤程度识别图。

图27是本发明实施例二中工况4mfcad指标损伤程度识别图。

图28是本发明实施例二中工况4mfcad指标模态阶数对损伤定位影响图。

图29是本发明实施例二中工况4mfcad指标模态阶数对损伤程度识别影响图。

具体实施方式

下面结合附图和实施例对本发明作进一步详细的描述。

参见图1，是本发明的振型加权模态柔度的梁结构损伤识别方法的流程框图，其具体步骤如下：

步骤1：通过模态测试分别获得梁结构损伤前、后的频率和振型；

步骤2：由损伤前、后的频率和振型计算振型曲率符号函数加权损伤指标，进行结构损伤定位；

步骤3：根据损伤前、后振型曲率符号函数加权损伤指标的相对变化计算梁结构节点损伤程度，进而计算得到单元损伤程度。

具体的，步骤1中，梁结构损伤前后模态测试各跨的测点数目不少于8个，并且损伤前后测点位置布置相同。

步骤1中，测试获得的模态阶数不少于3阶。

步骤1中，模态测试采用可测激励的方法，直接测得关于质量矩阵归一化的振型，或者采用仅测量输出的方法并通过梁结构的有限元模型建立质量矩阵，将振型对质量矩阵归一化后，可得到利用频率和振型表示的模态柔度矩阵mf：

其中，φ＝[φ1,φ2,l,φm]为振型矩阵，m为振型阶数，φi＝[φi1φi2lφin]^t为第i阶振型向量，n为测点数目，为对角矩阵，ωi为第i阶圆频率。

具体的，步骤2中，梁结构损伤前后的柔度变化矩阵为δ：

δ＝mfu-mfd(2)

其中，mfu和mfd分别为损伤前后的柔度矩阵，文中下标“u”、“d”分别表示未损伤状态和损伤状态。

为方便指标的说明，定义四个函数：diag(δ)表示取矩阵δ中的对角线元素，sum(δ)表示对矩阵δ中的元素按列求和，cur(δ)表示对矩阵δ中的元素按行求曲率，对于第i阶振型向量φi＝[φi1φi2lφin]^t，φij点的曲率可按如下公式进行计算：

其中，j为测点号，δl为测点j-1到测点j的间距与测点j到测点j+1间距的平均值。

sign(x)为符号函数，当sign(x>0)＝1，sign(x<0)＝-1，sign(x＝0)＝0。

均匀荷载面曲率差(changeinuniformloadsurfacecurvature，以下简记为ulsc)指标为将模态柔度矩阵按行(或列)加起来，再求损伤前后的曲率差，即：

|cur[sum(mfu)]-cur[sum(mfd)]|(4)

注意到ulsc指标式(4)中求和与求曲率运算可以交换顺序，故有：

|cur[sum(mfu)]-cur[sum(mfd)]|＝|sum[cur(mfu)]-sum[cur(mfd)]|＝|sum[cur(mfu-mfd)]|＝|sum[cur(δ)]|(5)

记由第i阶频率和振型构成的柔度矩阵为mfi，则：

其中，n为测点的数目。

式中：φi"表示第i阶振型的曲率，即

因：

则：

式中：为φi"的加权函数。

由式(5)：

于是，可以得到损伤指标的一种一般构造形式：

式中：c·φ″表示c中元素与φ″中对应位置元素相乘，当c为常数时c·φ″＝cφ″，ψu、ψd分别表示梁结构损伤前、后的振型曲率符号函数加权柔度矩阵，ψ＝[ψ(1)ψ(2)lψ(n)]^t。

当ci＝1时，为曲率模态改进方法c3指标，当时，为ulsc指标，当ci＝φi时，由式(6)可知，为对柔度矩阵取对角线元素操作，式(11)指标与diag|cur(δ)|指标相同，记为mfcd指标，同理可证，时，为sum|cur[cur(δ)^t]|，记为mfccsm指标，ci＝φi"时，为模态柔度差曲率矩阵，记为mfccd指标。

故通过式(11)中ci取不同的函数，可以构造并简化一些柔度曲率类指标。本发明构造另一个新的损伤指标，取权值函数ci＝sign(φi")，记该指标为振型曲率符号函数加权损伤指标mfcad(absolutediagonalofmodeflexibilitycurvature)，即：

可见，该指标直接使用振型曲率和圆频率进行计算，不必形成柔度矩阵，计算更加简便，该指标对振型曲率采用取绝对值后再相加，避免了多阶振型曲率直接相加，因符号不同产生的正负抵消问题。

进一步的，步骤3中，对于受弯梁，结构振动位移w与刚度的关系为：

式中：m(x,t)表示t时刻x位置弯矩，ei(x)表示x位置刚度，qi(t)表示模态坐标，w(x,t)表示t时刻x位置结构振动位移，下标“u”、“d”分别表示未损伤状态和损伤状态。

假定节点的损伤程度为dn(x)，则有：

eid(x)＝[1-dn(x)]eiu(x)(15)

假设损伤对梁的模态分布影响很小，即认为

qiu(t)＝qid(t)(16)

则联立以上公式可解得：

式中qiu(t)与时间有关，为使上式恒成立，应有：

即：

由于直接使用振型进行损伤识别，不能有效反应损伤程度，本发明采用加权柔度矩阵曲率代替振型曲率，使用式(20)进行节点损伤程度计算，当dn(x)<0时置dn(x)＝0。

对于静定结构，结构损伤前后弯矩不会发生变化，即mu(x,t)＝md(x,t)，故有：

对于超静定结构，结构发生损伤会导致一定的弯矩重分布，一般是损伤区域弯矩变小，由上式计算的损伤程度将比实际值偏小，本发明通过下式对超静定结构进行损伤程度修正：

由中心差分法计算得到的曲率为节点值，反映的是节点损伤程度，节点损伤程度与单元损伤程度的关系如图2所示，假定中间单元的损伤程度为de(x)，两侧左右单元的损伤程度de(l)＝de(r)＝0，则实际单元损伤引起的位移曲率曲线如图中“点线”所示，存在突变，由于数值计算无法考虑该突变，如中间单元左节点(2号节点)的节点损伤程度值为左右单元损伤程度的综合值，此处假定为二者的平均值，即：

w″de2l+w″de2r＝2w″dn2(23)

其中，w″de2l表示损伤状态2号节点左单元的位移曲率，w″de2r表示损伤状态2号节点右单元的位移曲率，w″dn2表示损伤状态2号节点位移曲率。

由式(20)可得：

使用ψ代替位移曲率w″，代入式(23)得

将de(l)＝0代入上式化简可得单元损伤程度与节点损伤程度的关系为：

其中de(x)为x位置单元损伤程度。

下面是应用本发明方法的具体工程实施例。以下的描述涉及附图时，除非另有表示，不同附图的相同数字表示相同或相似的要素。

实施例一：参见图3，为简支梁，其跨度10m，等分为20个单元(图中上排圆圈内的数字为单元编号，下排数字为节点编号)。截面尺寸为b×h＝300mm×500mm，材料弹性模量为e＝3.25×10⁴mpa，密度为2500kg/m³。单元的损伤通过弹性模量的降低来模拟，梁结构损伤工况如表1所示：

表1简支梁损伤工况

具体实施步骤如下：

步骤1：通过有限元模型仿真分析分别获得简支梁损伤前、后的前三阶竖向频率和振型。

步骤2：由损伤前、后的频率和振型按式(12)计算振型曲率符号函数加权损伤指标，进行损伤定位，参见图4、图5，由图4、图5可知，对于单损伤和多损伤工况，振型曲率符号函数加权损伤指标mfcad均能正确的进行损伤定位。

步骤3：根据损伤前、后振型曲率符号函数加权损伤指标的相对变化由式(21)计算梁结构节点损伤程度，再由式(26)计算得到单元损伤程度，如图6、图7所示，可见，除边单元20识别的损伤程度略小外，其它单元的损伤程度与理论值基本相同，损伤程度识别效果良好。

实施例二：参见图8，为一个三跨连续梁有限元模型，其跨径布置为10m+15m+10m，1.0m划分一个单元，一共35个单元，36个节点，(图中上排圆圈内的数字为单元编号，下排数字为节点编号)。截面尺寸为b×h＝300mm×500mm，材料弹性模量为e＝3.25×10⁴mpa，密度为2500kg/m³。单元的损伤通过弹性模量的降低来模拟，梁结构损伤工况如表2所示：

表2三跨连续梁损伤工况

具体实施步骤如下：

步骤1：通过有限元模型仿真分析分别获得三跨连续梁损伤前、后的前三阶竖向频率和振型。

步骤2：由损伤前、后的频率和振型按式(12)计算振型曲率符号函数加权损伤指标，进行损伤定位，如图9～图20所示，由图可知，对于单损伤工况，mfccd、mfcad指标的识别效果接近，相对较好，c3、ulsc、mfccsm指标次之，mfcd指标不能对支点处损伤进行识别；对于多损伤工况，c3指标只能识别两处损伤位置，ulsc、mfcd、mfccd指标能识别三处损伤，mfccsm、mfcad指标能识别全部五处损伤，mfcad指标的效果最好。

步骤3：根据损伤前、后振型曲率符号函数加权损伤指标的相对变化由式(21)计算梁结构节点损伤程度，再由式(26)计算得到单元损伤程度，如图21～图27所示，可见，对于单损伤工况，仅mfcad指标能较准确识别损伤程度，c3、ulsc、mfcd指标损伤程度存在明显异常峰值，mfccsm、mfccd指标损伤程度识别结果偏差大。对于多损伤工况，mfcad指标损伤程度识别效果良好。

上述分析时损伤指标均只采用前3阶竖弯模态计算得到，对工况4，分析采用不同阶数模态参数构造损伤指标时，损伤指标性能的变化情况。mfcad指标分别采用前1、3、5阶模态分析得到的损伤定位和损伤程度识别结果分别如图28、图29所示，可见，使用1阶模态时，只能识别三处损伤，损伤程度识别结果中存在异常峰值；3阶、5阶模态时，均能识别五处损伤并正确进行损伤程度识别，故mfcad指标仅需要3阶及以上模态即可正常进行损伤识别。

以上所述仅为本发明的两个实施例，凡依本发明申请专利范围所做的均等变化与修饰，皆属于本发明的涵盖范围。