一种不规则平面零件的分类和识别定位方法与流程

本发明涉及机械领域，特别涉及一种不规则平面零件的分类和识别定位方法。

背景技术：

目前工业机器人大多只能执行预设的指令动作，缺乏对作业环境的感知和应变能力，条件恶劣及复杂多变的作业环境极大地限制了机器人的应用。给工业机器人配备视觉系统，能够减少对机器人的运动轨迹规划以及离线编程，减少编程时间，提高生产效率。准确区分零件的种类以及对零件进行精准三维定位是视觉工业机器人准确抓取的一个重要前提，直接影响到加工零件的质量。在生产环境中，经常是多种零件混杂一起、位姿也各不相同，对于外形不规则的零件来说，定位尤为困难。目前主要是根据具体零件的形状和大小进行针对性定位设计，如在零件上做标记或制作专用定位模具，这种定位方法的生产成本高，定位繁琐，通用性不强。

技术实现要素：

本发明的目的在于克服现有技术中存在的缺点，提供一种通用性好、定位精度高、稳定性好、成本低的不规则平面零件的分类和识别定位方法。

本发明的目的通过下述技术方案实现：

一种不规则平面零件的分类和识别定位方法，是采用双目立体视觉系统，通过对相机标定后获取的左右图像进行立体匹配以获得视差图，并根据三角测量原理将视差图转换为三维点云数据，具体包括下述步骤：

(1)识别零件类型：使用双目立体视觉系统获取待测零件的图像，包括左图像和右图像，然后通过零件图像模板库对左图像待测零件进行匹配，识别零件的类型；

(2)获取视差图：使用凸多边形包围左图像的待测零件，计算凸多边形的质心，并以该质心为圆心绘制最大内切圆，然后以一定的比例因子绘制该内切圆的同心圆，再利用双目立体视觉系统获得该同心圆所在区域的视差图；

(3)平面拟合：将视差图转化为三维点云，再使用最小二乘算法对三维点云拟合平面，得到平面方程；

(4)待测零件的识别定位：利用所述平面方程，计算待测零件的三维位置和零件表面的平面法向量，进行识别定位。

步骤(1)中，所述通过零件图像模板库对左图像待测零件进行匹配，识别零件的类型，是采用形状匹配算法，具体识别步骤是：首先，创建每种零件的模板图像，制作图像模板库，同时假定左图像中存在位姿各异的各种零件；其次，在左图像中移动并以给定的旋转角度多次旋转模板图像，并多次计算模板图像与左图像的待匹配区域的相似度；找出该模板匹配时最大的相似度，对所有模板图像重复前面的操作，找出相似度最大时对应的模板零件类型作为待测零件的类型。

所述旋转角度是根据零件边缘的复杂程度、精度要求以及效率进行设定。旋转角度越小，则匹配精度越高，但匹配时间越长。如果零件的边缘较为平滑简单，可适当加大模板图像的旋转角度以提高效率。旋转角度优选1～5°。

所述相似度是指模板图像与左图像的匹配区域的对应位置的灰度平方差，具体表示为：假定用t表示模板图像，其中用t(x’,y’)表示模板图像任意点(x’,y’)的灰度值；同样地，用i表示左图像，其中用i(x,y)表示左图像任意点(x,y)的灰度值；相似度表示为：

式(1)中：n表示模板图像像素点的数量，r(x,y)表示左图像i上任一点(x,y)的相似度值，(x’,y’)指模板图像t中某一点的坐标。

步骤(2)中，所述的视差图，其获取方法如下：

(2-1)用凸多边形最小化包围步骤(1)识别出的零件；

(2-2)计算凸多边形的质心在左图像中的坐标；

(2-3)以所述质心为圆心绘制最大内切圆；

(2-4)以一定比例因子绘制上述内切圆的同心圆；

(2-5)利用双目立体视觉系统获得该同心圆所在区域的视差图。

所述的比例因子为最大内切圆半径的倍率，根据零件边缘的凹陷情况选择合适的比例因子，其大小在0～1之间，优选0.5～0.8。

其中，计算凸多边形的质心在左图像中的坐标，是采用下述方法：

(2-2-1)几何学中，三角形的重心为三条中线的交点，假定三角形三个顶点坐标(顺时针)依次为(x1,y1),(x2,y2),(x3,y3),重心坐标为(xg,yg),三角形的面积为s，有：

假定某均质物体的形状为三角形，不妨认为物体的质量就是三角形的面积，则质心抽象为三角形的重心；假定平面上有两个质点a和b，坐标分别为(xa,ya),(xb,yb),质量分别为ma和mb,这两点组成的系统的质心坐标为(xab,yab),质量为mab,则有：

mab＝ma+mb(7)

(2-2-2)对于任意凸多边形均可将它完全划分为三角形，假定凸多边形的顶点按顺时针依次为p1(x1,y1)，p2(x2,y2)，p3(x3,y3),......pn(xn,yn)，可将凸多边形分成δp1p2p3,δp1p3p4,δp1p4p5……δp1pn-1pn；

(2-2-3)根据上述公式，凸多边形的质心可通过递推的方法得出：先求δp1p2p3和δp1p3p4,各自的质心坐标和面积，再求δp1p2p3与δp1p3p4组合质心坐标和面积，然后求δp1p4p5的质心坐标和面积，再求δp1p2p3，δp1p3p4与δp1p4p5组合质心坐标和面积，直到求出δp1p2p3,δp1p3p4,δp1p4p5……δp1pn-2pn-1与δp1pn-1pn组合的质心坐标，最终得到的质心坐标则为所求凸多边形的质心坐标。

以质心为圆心绘制最大内切圆，采用的方法是：

(2-3-1)平面内直线方程采用一般直线方程a·x+b·y+c＝0表示，同一平面内的点(x0,y0)到该直线的距离d为：

(2-3-2)将凸多边形某相邻顶点坐标代入一般直线方程，求出经过这两相邻顶点的直线方程的系数a,b和c，将算出的质心坐标代入式(8)，算出质心到该直线的距离；

(2-3-3)按照上述的方法算出质心到凸多边形所有边长的距离，则距离最小值为最大内切圆的半径；假定凸多边形的质心坐标为(x0,y0),距离最小值为d0,该内切圆可表示为：

实际应用过程中，如果将零件所在区域的视差图直接转换成三维点云，会存在很多离群点，且大多出现在零件的边缘处，因为零件的边缘存在距离的突变。对零件进行凸多边形包围后再求最大内切圆，在相切处也可能存在部分零件的边缘。以一定的比例因子η绘制同心圆，所述比例因子η的取值范围为0～1，再将同心圆所在区域的视差图转换为三维点云的方法能够有效去除离群点，提高后续平面拟合的准确性。根据公式(9)，同心圆的方程可表示为：

(x-x0)²+(y-y0)²＝(ηd0)²(10)

所述同心圆所在区域的视差图的获取方法为：首先利用双目立体视觉系统获得与左图像一样大小的整张视差图，将视差图中像素点的坐标代入上述同心圆方程的左边，将得到的数值与同心圆半径的二次方比较大小，当数值大于同心圆半径的二次方时，则将该像素点的视差值赋值为0，当数值小于或等于同心圆半径的二次方时，则该像素点的视差值保持不变；对整张视差图的像素点做上述运算，得到同心圆所在区域的视差图。

步骤(3)中，所述平面拟合的具体步骤如下：

(3-1)利用式(11)将视差图中像素点的坐标(u,v)以及视差值d转换为左相机坐标系下(双目立体视觉的坐标系为立体校正后左相机的坐标系)的三维点云坐标(x,y,z)：

式(11)中，(ox,oy)是左相机光轴中心(即左相机坐标系的z轴与左图像的交点)在左图像中的像素坐标，f是立体校正后相机焦距(立体校正后左右相机具有相同的焦距f)，tx是左右相机的基线距离(基线距离为立体校正后左相机坐标系z轴与右相机坐标系z轴的距离)，这三个参数可通过对双目立体视觉系统进行立体标定来确定；

(3-2)然后使用最小二乘算法拟合三维点云中的平面，具体步骤如下：

(3-2-1)平面方程的一般表达式为：a·x+b·y+c·z+d＝0，(c≠0)，即：

令则：

z＝a0·x+a1·y+a2(13)

(3-2-2)用点(xi,yi,zi),i＝0,1,2,…,n拟合计算上述平面方程，则需要使s最小：

(3-2-3)要使得s最小，应满足：k＝0,1,2,即：

则有：

解上述方程组，就可得出平面方程z＝a0·x+a1·y+a2。

步骤(4)中，所述计算待测零件的三维位置和零件表面的平面法向量，具体方法如下：

(4-1)将步骤(2)得到的凸多边形的质心坐标代入步骤(3)得到的平面，可以计算出零件的三维坐标(x,y,z)；

(4-2)对于一般平面方程：a·x+b·y+c·z+d＝0，(c≠0)，其法向量步骤(3)得到拟合的平面方程为z＝a0·x+a1·y+a2；因此，零件表面的平面法向量可以表示为：单位化后为：

本发明与现有技术相比具有如下优点和效果：

(1)本发明采用模板匹配算法对零件进行分类识别，计算效率高。

(2)本发明采用零件的视差图来计算零件的三维位置和法向量，方法稳定和精度高。

(3)本发明通过对零件所在区域使用凸多边形包围，计算出凸多边形的质心，并以该质心为圆心绘制最大内切圆及同心圆，最后求出同心圆所在区域的视差图，这种方法能够有效去除离群点，提高后续平面拟合的准确性。

(4)本发明使用最小二乘算法拟合点云数据，得到平面方程，并根据平面方程计算零件的三维位置和法向量，本方法能够准确地拟合出三维点云中的平面，在不影响拟合结果的前提下去除大量的三维点云数据，运算速度快。

附图说明

图1为本发明的流程图。

图2为本发明的识别零件类型示意图。

图3为本发明的平面拟合示意图。

图4为本发明的拟合平面和点云的x-y视图。

图5为本发明的拟合平面和点云的x-z视图。

图6为本发明的拟合平面和点云的y-z视图。

图7为本发明的待测零件的定位结果示意图。

图8为本发明的待测零件的定位结果的x-z视图。

具体实施方式

下面结合实施例对本发明做进一步详细的描述，但本发明的实施方式不限于此。

实施例1

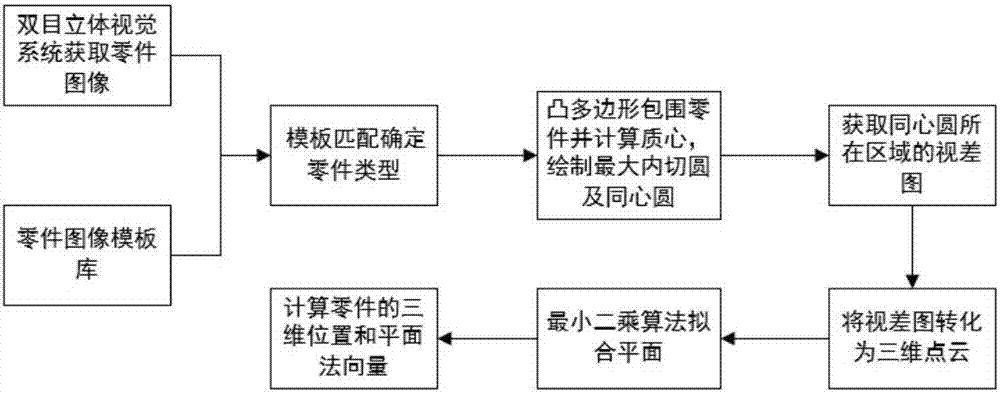
如图1所示，是本发明一种不规则平面零件的分类和识别定位方法的流程图。

首先，使用双目立体视觉系统获取零件图像；使用模板匹配算法将左图像中的待测零件图像与图像模板库进行匹配，确定零件的类型；然后，使用凸多边形包围零件，计算凸多边形质心，并绘制最大内切圆，再以最大内切圆半径的0.8倍比例因子绘制同心圆；使用双目立体视觉系统获取同心圆所在区域的视差图；利用公式(11)将视差图转换成三维点云；使用最小二乘算法拟合三维点云中的平面；最后，根据平面方程来计算零件的三维位置和平面法向量。

具体步骤如下：

步骤(1)：创建每种零件的模板图像，建立零件图像模板库，使用模板匹配算法识别左图像中待测零件，图2为识别零件类型示意图，其中共有4个零件均被识别出来，分为3种不同的零件：第1种零件有2个，用a1和a2表示；第2种零件有1个，用b1表示；第3种零件有1个，用c1表示。

步骤(2)：对识别出来的零件使用凸多边形包围，计算出各自的质心，绘制各自的最大内切圆，以最大内切圆半径的0.8倍绘制各自的同心圆，如图2所示，然后使用双目立体视觉系统依次获取各同心圆所在区域的视差图。

步骤(3)：利用公式(11)将得到的视差图转化为三维点云，再使用最小二乘算法对三维点云进行拟合平面，得到平面方程，如图3所示，黑色为点云数据，灰色为拟合的平面。图4为拟合平面和点云的x-y视图，图5为拟合平面和点云的x-z视图，图6为拟合平面和点云的y-z视图，从这几个图可看出拟合的平面出现在大部分点云聚集的区域内。

步骤(4)：将步骤(2)得到的凸多边形质心坐标代入步骤(3)得到的平面计算出零件质心的三维坐标。根据平面方程的系数使用公式(17)计算平面的法向量。图7是待测零件的定位结果示意图，其中的灰色直线为所求平面法向量。图8是待测零件的定位结果的x-z视图。

从图8可以看出大部分的点云聚集在高度为373～375mm之间，部分点云则偏离这个区域，但对平面的拟合影响不大，计算出来的平面能够准确地拟合到这个大部分点云聚集的区域，从图8的x轴上可看出同心圆的直径大概有53mm，而拟合平面附近上下的点云之间的高度间距只有1～2mm，可以说明这样的拟合效果是准确有效的。