基于Shearlet变换的多分量地震数据Corssline方向波场重建方法与流程

本发明涉及一种地球物理勘探方法，尤其是对海上地震拖缆采集到的稀疏地震数据进行重建的方法，主要是对采集的多分量地震数据的crossline方向进行重建。

背景技术：

当前海上地震数据拖缆采集，由于采集成本的限制，在crossline方向通常是不规则的并且是稀疏的，需要在有限的采集成本内覆盖较宽的观测范围，所以crossline方向采集间距通常是inline方向4倍以上。导致在crossline方向难以识别深层细小构造并且空间假频十分严重；实际中对这种波场进行插值也困难重重。

常规的地震数据插值要求假设地震数据同相轴是线性的，在时空域地震波波前认为是许多平面波的叠加，由此低频信息可以外推到高频信息上。为了使同相轴更加接近于线性，提出倾角时差校正和方位角时差校正的方法，但是受限于波场计算量很大。此外基于nyquist采样定理的方法的地震数据插值方法，要求采样频率至少是信号最高频率的二倍，否则就容易出现假频现象，影响数据的重建。这种思想应用在大多数插值方法中。然而海上地震数据采集中，crossline方向通常是格外稀疏的，基于nyquist采样定理的插值方法并不适用。

而在压力分量以外的测量垂直加速度以及crossline方向加速度的多分量地震采集技术近些年得到了应用。高质量的垂直分量能够使压力分量分解为上行波和下行波，因此可以提高获取的地震数据频带宽度。crossline方向的压力分量结合加速度分量使得真3d地震数据采集成为可能。vassalloand等人首次提出基于匹配追踪的多分量地震数据插值，其核心思想是利用sin基函数函数同时表示压力分量和加速度分量。

本发明有别于vassalloand技术方法，我们结合了两种能够基于稀疏变换的重建方法和多分量重建方法。

技术实现要素：

本发明的目的就在于针对上述现有技术的不足，提出一种基于shearlet变换的多分量地震数据crossline波场重建方法，以解决现有单分量地震crossline方向地震波场重建方法精度低，不能够有效重构地下细小构造、难以重建的问题。

本发明是通过以下技术方案实现的：

本发明的思想是：首先把地震数据重构问题归结于基于shearlet稀疏约束的l1正则化问题；其次，充分利用多分量测量中，压力和加速度同时被观测，在有限的观测序列，梯度为重构地震数据提供了额外的信息，能更精确的重构数据；采用交替迭代的方式，同时重构p及加速度波场。

基于shearlet变换的多分量地震数据corssline方向波场重建方法，是将shearlet变换与阈值迭代法相结合，地震数据插值归结为l1范数最优化方程：

x％＝argminx||x||1s.t.||y-ms^-1x||2≤ε(1)

上式中m为观测矩阵，m中元素为0表示数据缺失，元素为1表示数据存在，s-¹为shearlet逆变换；x为一组shearlet系数；

将地震数据插值转换到shearlet域重构出地震数据，反演出一组l1范数最小的shearlet系数x，公式(1)将地震数据采集系统作为观测系统，shearlet变换作为压缩感知理论实施的稀疏变换，构成了多分量地震数据插值的基础，在多分量地震数据插值中，引入了vy分量，由于

p和分量作为相互的约束条件，为彼此提供额外的插值信息，将p和同时作为插值输入，压力波场和加速度波场同时重建，将公式(1)与公式(2)相加得到：

观测到的压力和加速度分量作为已知输入，xp,xv分别为重构出压力波场和加速度波场的shearlet系数，每次迭代过程中p和相互更新，利用p的导数求取积分求取p。

基于shearlet变换的多分量地震数据corssline方向波场重建方法，包括以下步骤：

a、初始化迭代参数：迭代次数n,阈值因子lmax参数λ；

b、初始化压力波场以及梯度波场p＝0，

c、计算初始迭代参数δp＝λp·lmax，δv＝λv·lmax；

d、主循环fori＝1tondo；

e、利用基于shearlet变换的地震数据重构方法重建压力场和梯度场；

f、更新阈值参数δpandδv；

g、ifλp≤λmin&λv≤λmin结束.else返回d；

h、输出:重构的压力波场p以及速度波场

e步骤所述的重建压力场，包括以下步骤：

①、通过更新pi：

②、计算p波场的残差respi＝m(pm-pi)

③、通过阈值算法，求解压力波场的shearlet系数

④、通过shearlet逆变换更新压力波场pi+1＝sxi+1。

e步骤所述的重建梯度场，包括以下步骤：

i、通过pi更新

ⅱ、计算加速度波场的残差

ⅲ、通过阈值算法，求解加速度波场的shearlet系数

ⅳ、通过shearlet逆变换更新加速度波场

有益效果：本发明是利用多尺度shearlet变换表示地震数据，由于shearlet变换是一种具有方向性的各向异性小波，可以有效地捕捉地震数据的纹理特征，实现稀疏表示。并且该方法同时将压力分量和crossline方向速度梯度分量(即加速度分量)作为输入，速度梯度为压力分量提供额外信息，能够使得crossline方向重构更加精确。解决了现有单分量地震crossline方向地震波场重建方法精度低，不能够有效重构地下细小构造、难以重建的问题。解决了curvelet大曲率重构效果不好的问题。在采样数据特别稀疏的情况下重建地震数据；而且由于shearlet变换的多方向特性，噪声和信号在shearlet变换中的分布不同，噪声稀疏比较分散且幅值较小，而对数据信噪比要求不高；该方法区别于其他方法的最根本在于在传统单分量地震数据插值基础上拓展到了多分量地震数据插值，由于速度分量的加入增加了约束条件，能够取得更好的重建效果。地球物理数据处理和解释人员可借助程序包进行地震波场重构，具有较好的使用和推广价值。

附图说明：

图1是对合成数据进行插值测试效果比较图

(a)完整地震记录图，(b)缺失75％地震数据图，(c)基于小波变换的地震数据重建图，(d)基于curvelet变换的地震数据重建图，(e)基于小波变换的地震数据重建图，(f)基于shearlet变换的多分量地震数据插值图；

图2是对合成的3d数据沿crossline方向插值图，

a插值前的四个波场时间切片图，b插之后四个波场切片图c插值前波场的四个频率切片图，d插之后的四个波场频率切片图e为插值前全波场数据图f基于本方法重建的全波场图；

图3为对实际地震数据的三种方法处理对比图，

a为处理前的地震数据图，b为curvelet变换重构的地震数据图，c基于shearlet变换重构的地震数据图，d加入加速度分量约束的shearlet稀疏约束重建图；

图4为本发明的流程图。

具体实施方式：

下面结合附图和实施例作进一步的详细说明：

基于shearlet变换的多分量地震数据corssline方向波场重建方法，是将shearlet变换与阈值迭代法相结合，地震数据插值归结为l1范数最优化方程：

x％＝argminx||x||1s.t.||y-ms^-1x||2≤ε(1)

上式中m为观测矩阵，m中元素为0表示数据缺失，元素为1表示数据存在，s^-1为shearlet逆变换；x为一组shearlet系数；

将地震数据插值转换到shearlet域重构出地震数据，反演出一组l1范数最小的shearlet系数x，公式(1)将地震数据采集系统作为观测系统，shearlet变换作为压缩感知理论实施的稀疏变换，构成了多分量地震数据插值的基础，在多分量地震数据插值中，引入了vy分量，由于

p和分量作为相互的约束条件，为彼此提供额外的插值信息，将p和同时作为插值输入，压力波场和加速度波场同时重建，将公式(1)与公式(2)相加得到：

观测到的压力和加速度分量作为已知输入，xp,xv分别为重构出压力波场和加速度波场的shearlet系数，每次迭代过程中p和相互更新，利用p的导数求取积分求取p。

基于shearlet变换的多分量地震数据corssline方向波场重建方法，包括以下步骤：

a、初始化迭代参数：迭代次数n,阈值因子lmax参数λ；

b、初始化压力波场以及梯度波场p＝0，

c、计算初始迭代参数δp＝λp·lmax，δv＝λv·lmax；

d、主循环fori＝1tondo；

e、利用基于shearlet变换的地震数据重构方法重建压力场和梯度场；

f、更新阈值参数δpandδv；

g、ifλp≤λmin&λv≤λmin结束.else返回d；

h、输出:重构的压力波场p以及速度波场

e步骤所述的重建压力场，包括以下步骤：

①、通过更新pi：

②、计算p波场的残差respi＝m(pm-pi)

③、通过阈值算法，求解压力波场的shearlet系数

④、通过shearlet逆变换更新压力波场pi+1＝sxi+1。

e步骤所述的重建梯度场，包括以下步骤：

i、通过pi更新

ⅱ、计算加速度波场的残差

ⅲ、通过阈值算法，求解加速度波场的shearlet系数

ⅳ、通过shearlet逆变换更新加速度波场

在多分量海上数据采集中，加速度信息用来补充压力数据，运动方程揭示了压力p和加速度的比例关系：δp＝-ρa

式中ρ为介质的密度，

在inline和crossline方向，就有：

式中：vx，vy分别为inline方向和crossline方向的速度，标量上的点表示梯度，即为inline方向加速度，为crossline方向加速度。

将shearlet变换与阈值迭代法相结合，那么地震数据插值的问题归结如下的l1范数最优化方程：

x％＝argminx||x||1s.t.||y-ms^-1x||2≤ε(1)

上式中m为观测矩阵，m中元素为0表示数据缺失，而元素为1则表示数据存在。s^-1为shearlet逆变换；x为一组shearlet系数。

即将地震数据插值转换到shearlet域重构出地震数据，反演出一组l1范数最小的shearlet系数x，公式3将地震数据采集系统作为观测系统，而shearlet变换作为压缩感知理论实施的稀疏变换，通过最优化求解达到对地震数据的重构的目的。上面的求解方法构成了多分量地震数据插值的基础。在多分量地震数据插值中，我们引入了vy分量，由于

p和分量可以作为相互的约束条件，为彼此提供额外的插值信息，所以我们将p和同时作为插值的输入，压力波场和加速度波场同时重建，将公式(1)加入到公式(2)中，得：

在上述优化中，观测到的压力和加速度分量作为已知输入，xp,xv分别为重构出压力波场和加速度波场的shearlet系数，每次迭代过程中p和相互更新，利用p的导数求取积分求取p。

基于shearlet变换的多分量地震数据corssline方向波场重建方法的具体实施步骤如下：

a、初始化迭代参数：迭代次数n,阈值因子lmax参数λ；

b、初始化压力波场以及梯度波场p＝0，计算初始迭代参数δp＝λp·lmax，δv＝λv·lmax；

d、主循环fori＝1tondo；

e、利用基于shearlet变换的地震数据重构方法重建压力场和梯度场；

①、重建压力场

1、通过更新pi：

2、计算p波场的残差respi＝m(pm-pi)

3、通过阈值算法，求解压力波场的shearlet系数

4、通过shearlet逆变换更新压力波场pi+1＝sxi+1

②、重建梯度场

1、通过pi更新

2、计算加速度波场的残差

3、通过阈值算法，求解加速度波场的shearlet系数

4、通过shearlet逆变换更新加速度波场

f、更新阈值参数δpandδv.

g、ifλp≤λmin&λv≤λmin结束.else返回d.

h、输出:重构的压力波场p以及速度波场

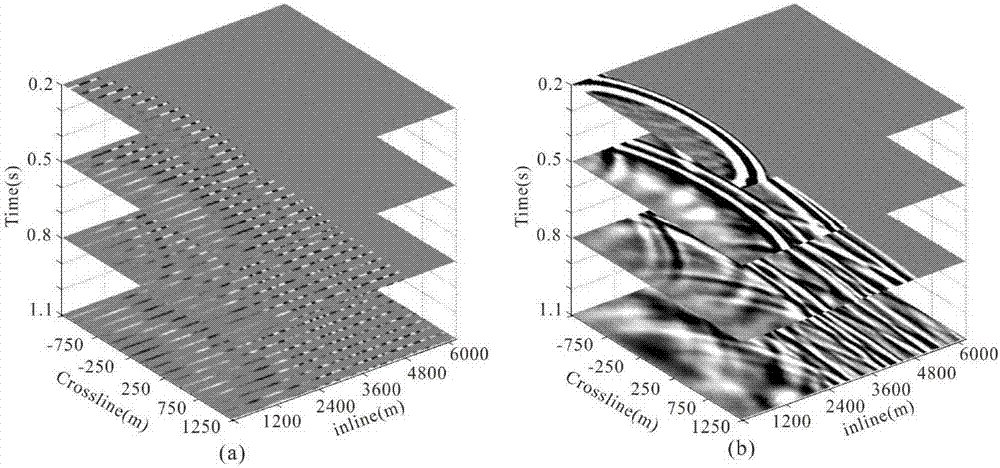
图1是对合成数据进行插值测试，(a)完整地震记录，(b)缺失75％地震数据，(c)基于小波变换的地震数据重建方法，(d)基于curvelet变换的地震数据重建方法，(e)基于小波变换的地震数据重建方法，(f)基于shearlet变换的多分量地震数据插值方法

图2为对合成的3d数据沿crossline方向进行插值，插值前道间距150m，插值后道间距25m，(a)插值前的四个波场时间切片，(b)插之后四个波场切片(c)插值前波场的四个频率切片，(d)插之后的四个波场频率切片(e)为插值前全波场数据(f)基于本方法重建的全波场。

图3为对实际地震数据的三种方法处理对比图，(a)为处理前的地震数据，(b)为curvelet变换重构的地震数据(c)基于shearlet变换重构的地震数据(d)加入加速度分量约束的shearlet稀疏约束重建方法。

图1c为经小波变换重构的结果，同相轴连续性不好，重构效果一般；图1d为经curvelet变换重构的结果，重构效果较小波变换有了较大的提升，但是在0.4s同相轴曲率大的部分效果欠佳；图1e为经shearlet变换重构的结果，是三种变换重构效果最好的，解决了curvelet大曲率重构效果不好的问题。由图1c-e表明，shearlet对地震数据表示最好。而图1f为加入加速度约束的地震数据重构方法，可以看出，加入了加速度约束后，重构精度得到了大幅度提升。

图2e为对合成的三维地震数据沿crossline方向进行插值，从图2a的四个时间切片可以看出，插值之前波场十分稀疏，而插值后的图2b中波场采集密度十分高，精度有了显著提升。图2a对应的fkk谱空间假频十分严重，而重建后的波场频谱有效地压制了假频信息。图2e-f展示了本发明的波场重建前后对比图。

图3a是用curvelet变换，shearlet变换对其压力分量进行插值得到图3b，图3c。图3d为插入了加速度分量约束得到的结果。从结果上来看，基于shearlet变换的多分量地震数据插值效果最好。

实施例1：

本发明实施例中首先使用了一个合成的3d数据，沿crossline方向进行插值，插值前道间距150m，插值后道间距25m，crossline方向有17缆，750采样点，压力波场重建前如图1a所示。用本发明对其进行1：6的重建。具体的实施步骤为：

a、抽取crossline方向的一个压力切片和加速度切片作为本发明的输入，设置迭代次数为50次，阈值因子0.99。

b、根据输入的数据计算迭代参数λ、δp＝λp·lmax和δv＝λv·lmax；

c、根据1:6的比例构建一个缺失矩阵m，大小为750*102；即17缆重构为102缆；

d、根据crossline方向的压力切片，加速度切片以及缺失矩阵m，对输入的压力波场和加速度波场做shearlet变换；

e、首先，对压力波场进行shearlet变换，进行shearlet阈值迭代方法更新压力波场shearlet系数对系数进行逆变换得到新的压力波场，通过公式δp＝-ρa得到更新加速度波场，其中ρ为水的密度；

f、其次，通过更新后的加速度波场进行阈值迭代，对加速度波场进行shearlet

通过公式δp＝-ρa得到新的压力波场；

g、重复步骤e-f直至满足误差条件输出压力波场和加速度波场；

h、重构出一个crossline方向压力切片进行下一个crossline切片重建，直至整个波场得到重建。

图1展示了本发明的波场重建前后对比图。图2a为对合成的三维地震数据沿crossline方向进行插值，从图2a的四个时间切片可以看出，插值之前波场十分稀疏，而插值后的图2b中波场采集密度十分高，精度有了显著提升。图2a对应的fkk谱空间假频十分严重，而重建后的波场频谱有效地压制了假频信息。

实施例2：以某海上实测数据为例，共设有40道，道间距为150m，先用curvelet变换，再用shearlet变换对其压力分量进行插值得到图3b，图3c。图3d为入了加速度分量稀疏约束得到的结果，从结果上看，基于shearlet变换的多分量地震数据插值效果最好。

具体实施步骤如下：

a、抽取crossline方向的一个压力切片和加速度切片作为输入，设置迭代次数为50次，阈值因子0.99。

b、将实际数据的压力波场和加速度波场作为本实例的输入

c、根据输入的数据计算迭代参数λ、δp＝λp·lmax和δv＝λv·lmax；

d、根据1:6的比例构建一个缺失矩阵m，大小为750*102；即17缆重构为102缆；

e、根据crossline方向的压力切片，加速度切片以及缺失矩阵m，对输入的压力波场和加速度波场做shearlet变换；

f、首先，对压力波场进行shearlet变换，进行shearlet阈值迭代方法更新压力波场shearlet系数对系数进行逆变换得到新的压力波场，通过公式δp＝-ρa得到更新加速度波场，其中ρ为水的密度；

g、其次，通过更新后的加速度波场进行阈值迭代，对加速度波场进行shearlet变换，同样根据shearlet阈值迭代方法更新得到加速度波场的shearlet系数对更新后的shearlet系数进行逆变换得到新的加速度，通过公式δp＝-ρa得到新的压力波场；

h、重复步骤e—f直至满足误差条件输出压力波场和加速度波场；输出:重构的压力波场p及速度波场