一种精确控制闭环光纤陀螺中2π电压参数的方法与流程

本发明属于光纤陀螺领域，具体涉及一种精确控制闭环光纤陀螺中2π电压参数的方法。

背景技术：

基于数字阶梯波反馈的闭环光纤陀螺由于其精度高、动态范围大、非线性度好等优势在光纤陀螺中得到了广泛的应用。但由于温度的影响，光纤陀螺的零偏和标度因数还是存在一定的变化，而这两个参数对于系统来说又尤为重要。其中，集成光学调制器(y波导)的2π电压随着温度的变化是引起光纤陀螺两个参数漂移的重要原因之一。因此，精确调整光纤陀螺中2π电压参数以适应2π电压的变化对于抑制光纤陀螺的温度漂移具有重要意义。

目前，在本征方波调制的光纤陀螺中，采用的主要方法是引入第二闭环来对2π电压参数进行伺服控制。第二闭环所依据的信号是阶梯波反馈信号2π复位时的误差信号。这就需要对阶梯波反馈信号的2π复位进行准确判定，以实现对2π电压的准确调整。

这就涉及到阶梯波的复位的判定方法以及2π电压参数调整方法。目前，常采用的阶梯波复位方法是利用d/a或寄存器的自动溢出实现2π复位，其对应的2π复位判定方法是通过判断阶梯波信号的高位(高1位或高几位)发生变化来判定阶梯波是否发生了复位：若高位发生变化(由1变0或由0变1)，则判定阶梯波发生了复位从而进行2π电压参数调整；若没有变化，则判定阶梯波没有发生复位，不进行2π电压参数调整。

该判定方法中存在一定的误判几率，即当光纤陀螺旋转速度较大或很大时，必然使得阶梯波台阶高度变大(台阶高度与旋转速度成比例关系)，可能会使得阶梯波信号高位发生了变化，但阶梯波并没有复位，也可能没有发生变化，确发生了复位。

下面举个例子：假如定义阶梯波信号是8位有符号数(定义无符号数原理类似)，则阶梯波信号的表示范围为：-2⁷～+2⁷-1(-128～+127)，下面分三种情况讨论：

1)在小角速率下，台阶高度小，即阶梯波变化幅度小(不会大于255)，假如台阶高度为5，某时刻阶梯波信号值为124，当阶梯波信号再上升时，阶梯波信号值为124+5＝129，但寄存器只能存小于127的数，129会自动溢出，变为-127(129-256),即阶梯波发生复位，并给出信号-127，通过比较复位前后阶梯波信号124和-127，可以看出高位是发生了变化，从而判定阶梯波发生了复位；

2)在大角速率下，台阶高度大，阶梯波变化幅度大，假如某时刻阶梯波信号值为124，若台阶高度为140，则当阶梯波信号再上升时，阶梯波信号值为124+140＝264，超过了127，必然发生了复位，复位后的值为264-256＝8，复位前后信号都为正，高位没有变化，或者台阶高度为255也会发生复位，复位后信号值为124+255-256＝123，复位前后信号值只差一个码，即复位前后信号值的高几位都没有变化，但阶梯波确实发生了复位，从而导致了漏判；

3)还有一种情况，是阶梯波信号跨越零点时，即阶梯波信号值负变正或正变负，高位会发生变化，如：某时刻阶梯波信号值为-3，若台阶高度为+10，则当阶梯波信号再上升时，阶梯波信号值为-3+10＝7，没有超过127，不会发生复位，但阶梯波信号高位发生了变化(符合位变了)，从而导致了误判；

从以上三种情况可以看出，通过判断阶梯波的高位发生变化来判定阶梯波发生复位存在漏判和误判的可能性，因此，探索新的阶梯波复位判定方法和调整2π电压参数的方法具有重要意义。

技术实现要素：

针对上述现有技术的不足，本发明所要解决的技术问题是：提供一种精确控制闭环光纤陀螺中2π电压参数的方法，能够准确的判定阶梯波是否发生复位以及2π电压参数是否准确，从而精确调整光纤陀螺的2π电压参数，减小光纤陀螺的温度漂移，提高光纤陀螺的精确度。

为解决上述技术问题，本发明采用的一个技术方案是：一种精确控制闭环光纤陀螺中2π电压参数的方法，其特征在于，包括以下步骤：

1)通过y波导对输入光纤环的光波进行本征方波调制和阶梯波反馈闭环，并分别对本征方波的正负调制半周期内到达探测器的光波的光功率进行采样，得到阶梯波没有复位时，光纤陀螺基于本征方波调制后的奇偶采样值为：

在阶梯波复位时，光纤陀螺基于本征方波调制后的奇偶采样值为：

式中：p0为光纤陀螺绝对静止时到达探测器的光功率；φs为旋转引起的相位差；фm为方波调制信号，其值为+ф0或-ф0，φ0为方波调制幅度；φf为闭环反馈相位，φfw为阶梯波复位期间引入的相位差，当2π电压参数准确时，其满足：

φfw＝φf±2π*k；

式中k为正整数；其中，当φf为正时，上式取负号；当φf为负时，上式取正号；

2)将复位中的奇/偶采样值对应与复位前或后的奇/偶采样值相减，得到：

奇奇相减：

偶偶相减：

当2π电压发生变化时，δp2π≠0，由此可以通过伺服控制对2π电压参数进行调整，以适应新的2π电压；

3)将δp2π作为2π电压调整信号对2π电压参数进行伺服控制：

d2π(2)＝d2π(1)+k*δp2π；

式中：d2π(1)为伺服控制前原2π电压参数，d2π(2)为伺服控制后新2π电压参数，k为系数。

与现有技术相比，本发明具有如下优点：本发明能够简单有效并且准确地判断阶梯波是否复位，从而准确的判断2π电压参数是否准确，进而更为精确地进行2π电压参数的调整，以适应新的2π电压，减小光纤陀螺的温度漂移，从而提高光纤陀螺的测量精确度。

附图说明

图1是光纤陀螺光路结构框图。

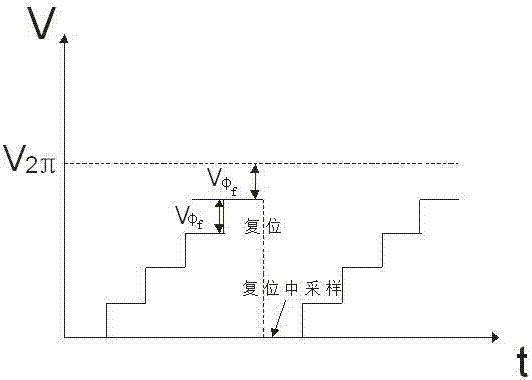
图2为上升阶梯波示意图。

图3为下降阶梯波示意图。

具体实施方式

下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。

一种精确控制闭环光纤陀螺中2π电压参数的方法，其中，参见图1，光纤陀螺包括光源、探测器、耦合器、y波导、光纤环以及fpga控制芯片。

具体控制方法包括以下步骤：

1)通过y波导对输入光纤环的光波进行本征方波调制；

方波调制下到达探测器光功率可用下式表达：

式中：p0为光纤陀螺绝对静止时(φs＝0)到达探测器的光功率；φs为旋转引起的相位差。

式中：φm为：

式中：φ0为方波调制幅度，τ为光纤环的渡越时间(光波在光纤环中传输一周的时间)。

分别对本征方波的正负调制半周期内光波到达探测器的光功率进行采样，从而得到y波导在调制周期的奇偶采样值：

奇偶采样值相减得：

δp＝p--p+＝p0sinφ0sinφs；.............................(4)；

由于方波调制幅度一旦确定即为定值，因此p0sinφ0为常数项，可用a表示。另一方面，当φs为小量时，有sinφs＝φs，于是奇偶采样的差值为：

δp＝aφs；.............................(5)；

由(5)式可知，方波调制下奇偶采样的差值与旋转引起的相位差成正比，可以作为旋转角速率输出，同时通过闭环控制将总相位差伺服控制的零附近。从而得到光纤陀螺闭环控制后的奇偶采样值为：

式中：φf为闭环反馈相位，其满足：

φf＝-φs；.............................(7)

因此，(6)式也可表示为：

2)通过y波导对光纤环的输出光进行阶梯波反馈；

阶梯波闭环反馈是通过在y波导调制器的电极上引入阶梯波信号利用晶体的压电效应实现的。y波导就是由铌酸锂晶体制成的，该晶体上施加电压时通过它的光波就会产生相位差；该相位差与电压大小成正比。

如图1所示的光纤陀螺光路结构，光源发出的光波经过y波导时被调制信号调制一次，经过光纤环传输后返回y波导时再次被调制(同时对后续的光波进行第一次调制)，两次调制的时间间隔为光纤环传输光波时间，即渡越时间。由于两次调制时两束光波的传输通道发生了交换，因此，真正引入光路中的相位差为两次调制相位差的差值(以下简称为调制相位)。即调制相位为调制电压波形以光纤环渡越时间为步长的一阶差分。因此若要产生恒定的反馈相位差φf，必须使反馈电压信号不断上升或下降(上升对应正，下降对应负)，其中上升或下降的幅度与反馈相位差对应，根据这一原理可以得到闭环控制的实现为在y波导上施加如下反馈波形：

或者：

式中vφf为对应于相位差φf的电压值，(9)式表示引入正向相位差(阶梯波上升)，(10)式表示引入负向相位差(阶梯波下降)。

上述波形呈台阶形状，称为阶梯波，图2和3为阶梯波的示意图。阶梯波不能无限上升或下降，必然要进行复位，复位的电压差引入的相位差和阶梯波正常上升或下降引入的反馈相位差之间必须相差2π或2π的整数倍，才不会引起复位旋转误差。即复位时，探测器信号为：

式中φfw为阶梯波复位期间引入的相位差，当2π电压准确时，其满足：

φfw＝φf±2π*k；.............................(12)

式中k为正整数(实际应用中一般取1)，上式中正负号的取法为：当φf为正时，上式取负号；当φf为负时，上式取正号。

通过比较(8)式和(11)式可以看出，当光纤陀螺的2π电压准确时，根据三角函数的周期性，可以看出，在复位期间不会引入复位误差。然而当光纤陀螺的2π电压发生变化时(特别是当温度变化时)，会引入复位误差。因此，根据复位前后，复位误差大小引入第二闭环对2π电压进行伺服控制是十分必要的。

3)当2π电压不准确时，将复位中的奇偶采样值对应与复位前或后的奇偶采样值相减，得到：

奇奇相减：

偶偶相减：

当2π电压发生变化时，δp2π≠0，由此可以通过伺服控制对2π电压参数进行调整，以适应新的2π电压。

4)将δp2π作为2π电压调整信号对2π电压参数进行伺服控制：

d2π(2)＝d2π(1)+k*δp2π；.............................(15)

式中：d2π(1)为伺服控制前原2π电压参数，d2π(2)为伺服控制后新2π电压参数，k为系数。

下面以奇减奇为例，进行公式推导(偶减偶只需将φ0换成-φ0即可)：

根据公式(8)，可设前一奇调制周期的采样值为：

后一奇调制周期的采样值为：

式中，φ1为前一奇调制周期闭环反馈相位，φ2为后一奇调制周期闭环反馈相位，两反馈相位满足：

将(16)式和(17)式相减得：

下面对(19)式进行分析，

a)假如没有两个奇采样时间段内都没有发生复位，则有(19)式必然为零；此时2π电压是否准确，也无法获知(这也是本征方波调制陀螺的局限性，只有复位时才能察觉2π电压是否准确)，这不需要任何2π电压参数的操作；

b)假如发生复位，对于2π电压准确来说，将(12)、(18)代入(19)式，其结果必然为零，此时也不需要任何2π电压的操作；

c)假如发生复位，对于2π电压不准确来说，(19)式中第二项必然不等于零，至于第一项对于特定点(特殊的旋转速度、特殊的调制幅度、特殊的复位相位组合来说)可能为零，但这些点是不稳定的，旋转速度稍微变化或者环境因素等会使得不稳定，因此在实际中，上述情况是不存在的，即第二项不为零，也就是说(19)式不为零。此时需要对2π电压参数进行伺服控制以实现2π电压参数的调整。

结合a)、b)、c)可以得到以下结论：

奇减奇(或者偶减偶)的差值为零时，表明阶梯波没有复位或者阶梯波复位了但2π电压准确，不需要任何2π电压的操作；奇减奇(或者偶减偶)的差值不为零时，表明阶梯波确实发生了复位且2π电压不准确，需要根据(15)式对2π电压参数进行伺服控制以实现2π电压参数的调整。

本发明实施方式，通过实时监测光纤陀螺中奇奇差值，当上述差值不为零位时，则表明阶梯波发生了复位，并将差值作为2π电压调整信号进行电压的伺服闭环控制，能够准确判定是否产生复位，并且根据误差参数来调整2π电压参数；从而提高光纤陀螺的精确度。

以上仅为本发明的实施方式，并非因此限制本发明的专利范围，凡是利用本发明说明书及附图内容所作的等效结构或等效流程变换，或直接或间接运用在其他相关的技术领域，均同理包括在本发明的专利保护范围内。