互耦条件下双基地MIMO雷达角度估算方法与流程

本发明涉及一种雷达信号处理技术，具体的说涉及一种互耦条件下双基地mimo雷达角度估算方法。

背景技术：

伴随着多输入多输出(multiple-inputmultiple-output,mimo)技术在移动通信领域的不断成功与发展，mimo技术在雷达领域应用的研究方兴未艾。利用匹配滤波处理及虚拟通道的思想，mimo雷达可获得远优于传统相控阵雷达系统的新能。mimo雷达技术是学术界、工程界的研究热点之一，该研究方向不仅有重大的理论和学术意义，而且应用前景广阔，特别是具有巨大军事应用价值和民用价值，美、英、日等科技强国均把它作为发展未来智能化探测系统的重点突破的技术。为了对敌目标进行有效监测与阻击，需要雷达系统能够快速、精确对敌目标进行定位。联合波离角(direction-of-departure，dod)和波达角(direction-of-arrival，doa)估计是mimo雷达目标定位的基本任务之一，因而引起国内外学者的广泛关注。迄今为止，已涌现大量优秀的角度估计算法。典型的mimo雷达角度估计算法有谱峰搜索法、求根方法、基于旋转不变技术的估计算法、传播算子法、张量方法、稀疏表示法等。其中，张量类算法由于能够挖掘mimo雷达数据的结构相关特性，因而是近几年的研究热点。

然而，现有算法的优异性能均是在理想的阵列条件下获得的。实际上，由于雷达系统往往在非理想的环境下，因而上述算法在实际工程中难以获得理想的性能。阵列mimo雷达的非理想环境之一是阵元互耦影响，其主要表现为相邻的几个阵元间数据的相互影响。为克服mimo雷达阵列的互耦效应，已有部分学者开展这方面的研究，特别是无需校准源的参数估计方法。刘志国等人提出一种基于capon算法和迭代思想的dod与doa及互耦估计算法(刘志国,廖桂生.双基地mimo雷达互耦校正[j].电波科学学报,2010,25(4):663-667)，liu等人提出了一种基于降维music的算法(liuxl,liaogs.directionfindingandmutualcouplingestimationforbistaticmimoradar[j].signalprocessing,2012,92(2):517-522)。上述两种算法均将角度估计转换为二次优化的问题，虽然可有效降低运算量，但是谱峰搜索过程仍然具有较大的复杂量。此外，由于二次优化求解目标角度过程中，阵列受互耦的影响可能会产生模糊效应，因而角度估计的精度可能会严峻下降。利用互耦矩阵的对称toeplitz结构，zheng等人提出了一种基于esprit的双基地mimo雷达角度估计算法(zhengzd,zhangj,zhangjy.jointdodanddoaestimationofbistaticmimoradarinthepresenceofunknownmutualcoupling[j].signalprocessing,2012,92(12):3039-3048)，通过选择性矩阵可以消去阵列的互耦效应。为利用阵列数据的多维结构，wang等人提出了一种基于实值高阶子空间分解(higher-ordersingularvaluedecomposition，hosvd)算法(wangxp,wangw,liuj,etal.tensor-basedreal-valuedsubspaceapproachforangleestimationinbistaticmimoradarwithunknownmutualcoupling[j].signalprocessing,2015,116:152-158)，尽管使用实值计算，但是hosvd仍然存在计算复杂度大的问题。wen等人则提出一种基于三线性分解的dod与doa估计算法(wenfq,xiongxd,zhangzj.angleandmutualcouplingestimationinbistaticmimoradarbasedonparafacdecomposition[j],digitalsignalprocessing,2017,65,1-10)，其可改善张量分解的精度和计算复杂度。wang等人则提出一种基于张量压缩和稀疏表示的双基地mimo雷达角度估计算法(wangxh,zhangg,wenfq,etal.angleestimationforbistaticmimoradarwithunknownmutualcouplingbasedonthree-waycompressivesensing[j].journalofsystemsengineeringandelectronics,2017,28(2):1-9)，该算法适合大规模阵列的参数估计。此外，上述二种算法均是使用复数运算，并不适合实际工程中的雷达系统。

考虑到均匀阵列的旋转不变特性和互耦矩阵的toeplitz对称特性，本发明提出一种基于改进三线性分解的双基地mimo雷达角度估计算法。首先利用选择性矩阵消去阵列互耦效应，然后构建阵列数据的三线性分解模型。考虑到均匀线性阵列(uniformlineararray，ula)的中心对称特性，利用前后平滑技术对张量数据进行处理，再构造阵列的增广输出的三线性分解模型。利用三线性分解获得相关导引矢量的估计，最后再利用阵列的旋转不变特性恢复目标的dod与doa。由于三线性分解使用迭代的方式获得相关导引矢量，因而能获得比hosvd更高的估计精度。且阵列增广输出为实数，故本算法仅涉及实数运算，相比已有复数算法，本发明算法的计算复杂度更低。

技术实现要素：

鉴于以上原因，有必要提供一种能够自动配对目标角度，并使用算法处理相干源，而且适用于实际工程中的硬件运算的互耦条件下双基地mimo雷达角度估算方法。

本发明提供一种互耦条件下双基地mimo雷达角度估算方法，其特征在于，所述互耦条件下双基地mimo雷达角度估算方法包括如下步骤：

s1、对接收阵列数据进行匹配滤波处理，并构建一个三阶张量模型；

s2、根据互耦矩阵的部分子矩阵的行元素具有循环移位特性构造去耦矩阵，对三阶张量模型进行去耦运算；

s3、根据阵列方向矩阵中导引矢量的中心对称特性，构造前后平滑的数据张量，并经过酉变换获得实数张量；

s4、对实数张量进行分解，构建去耦后数据的增广输出三线性模型，对三线性模型进行拟合，将联合dod与doa估计与三线性模型相联系；

s5、通过最小二乘方法估计目标的dod与doa。

本发明所述互耦条件下双基地mimo雷达角度估算方法，其利用阵列信号的多维结构，将匹配滤波后的雷达数据表述成一个三阶张量模型。考虑到均匀线性阵列互耦矩阵的带状toeplitz特性，利用部分阵元方向矩阵具有共同的尺度变换特性消除互耦的影响。结合前后平滑技术和酉变换技术，构建去耦后数据的增广输出三线性模型，再将联合dod与doa估计与三线性模型相联系。最后，通过最小二乘方法估计目标的dod与doa。所述互耦条件下双基地mimo雷达角度估算方法，其与传统算法相比，能有效应对收发阵列存在互耦的场景，无需额外的校准源、奇异值分解以及谱峰搜索；还能够自动匹配所估计的dod与doa；且通过采用三线性分解仅涉及实数运算，降低计算复杂度；同时对相干源仍然适用。

附图说明

图1是双基地mimo雷达角度估计示意图；

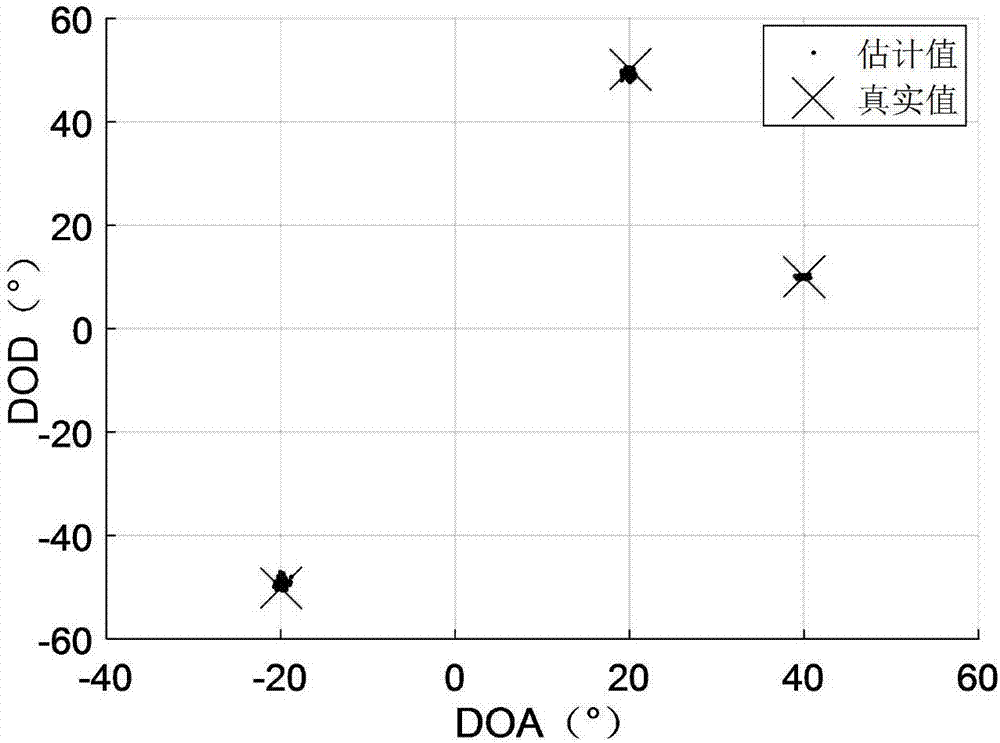
图2是在弱互耦、非相干源、snr＝-15db时，本发明所述互耦条件下双基地mimo雷达角度估算方法的散点图；

图3是在强互耦、相干源、snr＝-10db时，本发明所述互耦条件下双基地mimo雷达角度估算方法的散点图；

图4是弱互耦、非相干源时，本发明所述互耦条件下双基地mimo雷达角度估算方法与其他算法rmse性能对比；

图5是弱互耦、非相干源时，本发明所述互耦条件下双基地mimo雷达角度估算方法与其他算法psd性能对比；

图6是强互耦、非相干源时，本发明所述互耦条件下双基地mimo雷达角度估算方法与其他算法rmse性能对比；

图7是强互耦、非相干源时，本发明所述互耦条件下双基地mimo雷达角度估算方法与其他算法psd性能对比；

图8是强互耦、相干源时，本发明所述互耦条件下双基地mimo雷达角度估算方法与其他算法rmse性能对比；

图9是强互耦、相干源时，本发明所述互耦条件下双基地mimo雷达角度估算方法与其他算法psd性能对比。

具体实施方式

为了使本发明的目的、技术方案及优点更加清楚明白，以下结合附图及实施例，对本发明进行进一步详细说明，应当理解，此处所描述的具体实施例仅仅用以解释本发明，并不用于限定本发明。

本发明提供一种互耦条件下双基地mimo雷达角度估算方法，所述互耦条件下双基地mimo雷达角度估算方法包括如下步骤：

s1、对接收阵列数据进行匹配滤波处理，并构建一个三阶张量模型；

s2、根据互耦矩阵的部分子矩阵的行元素具有循环移位特性构造去耦矩阵，对三阶张量模型进行去耦运算；

s3、根据阵列方向矩阵中导引矢量的中心对称特性，构造前后平滑的数据张量，并经过酉变换获得实数张量；

s4、对实数张量进行分解，构建去耦后数据的增广输出三线性模型，对三线性模型进行拟合，将联合dod与doa估计与三线性模型相联系；

s5、通过最小二乘方法估计目标的dod与doa。

具体的，首先引入关于张量操作的三个定义：

定义1(张量展开)：令为一个n阶张量，x的模-n(n＝1,…,n)矩阵展开表示为[x]n。其中，位于张量x的(i1,…,in)位置的元素成为位于矩阵[x]n的(in,j)处的元素，

定义2(模-n张量与矩阵乘积)：定义n阶张量与矩阵的模-n乘积为其中且

定义3(张量模乘性质)：n阶张量的模乘性质主要有如下两条：

x×n·a×m·b＝x×m·b×n·a,m≠n

x×n·a×m·b＝x×n·(b·a)表达式(1)

式中，(·)^t表示转置。

假设一个双基地mimo雷达的阵列模型，如附图1所示。其中mimo雷达的天线系统由m个阵元和n个接收阵元构成，二者均是ula。假设收发阵元间距均为d，为不引起阵列相位畸变需d≤λ/2，为发射信号波长，在本发明中假设d＝λ/2。发射阵元发射相互正交的波形。假设发射天线发射的基带信号为相互正交的编码波形，其中第m(m＝1,…,m)路基带信号为且满足

其中，q为编码码长，(·)^h表示共轭转置。假设在雷达远场处于同一个距离元内具有k个目标，第k(1≤k≤k)个目标的方位为其中为目标的dod，θk为目标的doa。假设收、发阵列相邻的p+1个阵元间存在互耦效应，互耦系数分别为cr＝[1,cr1,…,crp]^t和ct＝[1,ct1,…,ctp]^t，其中0＜|crp|＜…＜cr1<1，0＜|ctp|＜…＜ct1＜1。收、发阵列互耦矩阵可以分别用cr和ct表示，其分别为对称toeplitz矩阵。以p＝1为例，cr具体形式如下

考虑mimo雷达的一个相干处理时间(coherentprocessinginterval，cpi)包含l个脉冲，则第l(l＝1,2,…,l)个脉冲时间的接收阵列的输出信号为

xl＝crardiag(bl)(ctat)^ts+wl表达式(3)

其中，分别为接收方向矩阵和接收导引矢量；为第l个脉冲目标回波特性矢量，diag(·)表示对角化运算；分别为发射方向矩阵和发射导引矢量；为发射信号矩阵；为接收阵列天线接收的噪声矩阵，在本发明中被假设为均匀白噪声。令对每个接收天线的接收数据分别用进行匹配滤波处理，则匹配滤波器输出的l个cpi的结果为

其中⊙表示khatri-rao积，b＝[b1,b2,…,bl]^t为目标特性矩阵。为匹配滤波后的噪声矩阵，el＝vec(wls^h)/q，vec(·)表示矢量化操作。分别表示受互耦影响的方向矩阵。利用tucker张量模型，表达式可以重新表述成一个阶数为3、秩为k的张量：

上式中，ik表述维数为k×k的单位张量，e表述噪声张量。结合定义1可以看出即表达式(4)中的矩阵为(5)式中的张量的模-3展开。注意到，由于收发阵列均受到互耦的影响，此时不再为vandermonde矩阵，因而互耦影响下已有高分辨估计算法会失效。

通过分析互耦矩阵可知，互耦矩阵的部分子矩阵的行元素具有循环移位特性(仍以p＝1时的cr为例，虚线框内的子矩阵，其每一行均是上一行向右移一位的结果)。令考虑到互耦矩阵的这种特性，构造如下去耦矩阵

式中0表示元素全为0的矩阵，i表示单位矩阵，下标均表示矩阵的维数。容易得知0：

上式中分别为仅与θk、有关的系数，其可被视为尺度变换因子。分别为ar(θk)、的前行、行元素构成的中心对称向量(例如则结合定义2与定义3，可将本发明去耦的方式表述成张量运算的形式

式中d＝diag(dt)·diag(dr)，上述过程可以看作是去耦合过程，经过该过程后，阵列方向矩阵重新获得旋转不变特性(对阵列旋转不变特性没有影响，故与b矩阵表述在一起)。

表达式(7)中的张量z为复数张量，考虑到中导引矢量的中心对称特性，可以利用前后平滑技术和酉变换计算进一步降低参数估计的复杂度。的中心对称特性可以表述成

上式中，表示维数为的反向交换矩阵，其反对角线元素为1，其余元素为0；令结合表达式(7)、表达式(8)和定义3有

式中，为相应的噪声张量。通过前后平滑技术可以构建接收数据的增广输出，张量数据的前后平滑可以表述成如下形式

上式中，∪3表示将两个数据张量按照模-3方向进行堆叠，通过上述张量平滑过程后，具有中心对称结构0。通过酉变换技术，可以将上述复数张量变换为实值张量，具体过程可表述为

上式中，表述维数为的酉变换矩，其具体形式如下：

以为基数为例，有

故通过酉变换后的向量为一个实数向量。结合表达式(10)、表达(11)和定义3有

上式中，e^r为经过酉变换后的实值张量。

上述变换后的方向矩阵中含有目标相关信息，如果能获得这些矩阵的估计，则可进一步获得目标参数的相关估计。在传统基于子空间方法的角度估计算法中，往往首先将上述张量转换为矩阵的形式，然后对矩阵进行分解获得目标的信息。这些方法往往无法利用张量数据的多维结构信息，通过张量分解的方式往往能获得更加精确的参数估计性能。现有的张量分解方法主要有两大类：直接法(如hosvd)和迭代法(三线性分解法)。直接法将张量运算转化为多个子空间分解运算，其计算复杂度往往较大，而迭代法往往通过几次低维的迭代获得高精度的参数估计。三线性分解又称为平行因子分解(parallelfactordecomposition，parafac),是一类重要的张量分解方法，本发明采用(trilinearalternateleastsquares，tals)进行张量分解，具体过程如下节所述。

令根据定义1，表达式(12)中的张量可以展开成如下矩阵的形式：

上式中，e1＝[e^r]1，e2＝[e^r]2，e3＝[e^r]3。式(13)即为三线性分解模型的矩阵表达形式，由于z^r中每个索引位置的元素是由三个矩阵的元素的乘积构成，因此可认为z^r具有三个方向。相应地，z1、z2和z3分别可被视为将张量数据z^r沿着发射方向、接收方向和脉冲方向展开而获得的矩阵。传统的子空间分解法往往仅利用了张量的数据的某一个方向展开的信息。

tals算法是一种高效的三线性分解模算法，其采用最小二乘(leastsquares，ls)代价函数依次交替的拟合三个矩阵，当拟合误差达到预期范围内时算法终止。其处理本发明所述三线性模型的具体步骤如下，a)假设z1、z2和z3中的两个矩阵已知，采用ls的方法拟合其中的任何一个矩阵，b)采用ls的方法拟合剩下的两个矩阵，c)重复a)和b)直到迭代次数达到预设值或拟合误差达到预设阈值。现以某次具体的迭代过程说明tals的迭代过程，根据式(13)可知，对atr拟合的代价函数为

其中，||·||f表示矩阵的frobenius范数。根据上式易知，atr的ls估计值为

式中分别是在上一次迭代后所获得的br和arr的估计值。类似的，可以构造arr拟合函数和其ls估计

式中为在本轮迭代过程中获得的atr的估计值，为上一轮迭代后获得的br的估计值。同理，可以构造br的拟合代价函数和其ls估计

其中分别是本轮迭代过程中获得的arr、atr的估计值。重复上述过程直到达到算的迭代条件即可获得对相关矩阵的估计。

由于tals算法在更新过程中arr、atr及br的误差将得到改善或者保持不变，但是不可能增大，因而tals总是会收敛的。tals的收敛速度与相关矩阵的初始化优劣密切相关，一般使用随机初始化矩阵将获得较慢的收敛速度，而使用esprit算法可加快算法收敛。此外，使用一些压缩算法可以进一步加快算法收敛。本发明在实际仿真中使用comfac算法，其主要是通过张量压缩的方法降低迭代计算的复杂度，一般仅需若干次迭代算法便可快速收敛。

唯一性是三线性分解的重要特征之一。定理1给出了三线性分解的唯一性的条件：

定理1：对于(13)式中的三线性模型，假设的k-秩分别为若其满足

则除了列模糊和尺度模糊之外，通过三线性分解获得的atr，arr和br是唯一的。若分别为atr，arr和br的估计值，则定理中的列模糊和尺度模糊可以表示为

其中ω是一个列置换矩阵，n1，n2和n3分别对应的估计误差矩阵，δ1，δ2和δ3为三个对角矩阵，其对角元素分别表示相应的尺度因子，且其满足δ1δ2δ3＝ik。经过tals过程，可获得atr和arr的估计值由于因此可利用酉变换后阵列的旋转不变特性来还原目标角度的相关信息，其可表述为如下的形式：

上式中，ψt＝diag(gt)，ψr＝diag(gr)，gt＝[gt1,gt2,l,gtk]^t，gr＝[gr1,gr2,l,grk]^t，grk＝tan(πsinθk/2)，k＝1,2,…,k。其它旋转性矩阵分别为：

其中，re{·}、im{·}分别为取实部和虚部。根据表达式(20)，ψt与ψr中第k(k＝1,2,…,k)个对角元素gtk、grk的ls估计值分别为

其中，分别为的第k列。进一步，第k个目标的dod与doa的估计分别为

其中arcsin(·)与arctan(·)分别为反正弦与反正切运算。根据表达式(19)与表达式(20)可知，具有同步的列置换运算，因而是自动配对的。

本发明分析的计算复杂度主要是以复数乘法运算的次数为依据，算法的计算复杂度的具体分析如下。对z^c进行酉变换的运算量为由于实数运算的复杂度为复数运算复杂度的1/4，因而tals的运算量为其中l是迭代的次数。一般说来，tals算法迭代若干次以内便可以达到收敛的要求。计算的复杂度为

表1列举了本发明算法与现有文献music、esprit、hosvd及parafac算法复杂度的对比。

表1

可以看出music算法的运算量最大，其在谱峰搜索和奇异值分解过程中均计算量大；esprit和hosvd的复杂度主要集中在特征值分解，其复杂度的最高阶数均为故计算过程仍然较为复杂。采用迭代方法的parafac算法和本发明算法的复杂度主要集中在tals过程，且运算量的最高阶数远小于由于采用实数运算，本发明算法的迭代运算量小于parafac方法。

表达式(18)给出了本发明算法的可辨识度条件，即目标数目辨识的上限。一般来说，因而本发明算的最多可辨识个目标，而现有文献中的parafac算法最多可辨识个目标。因而在相同的条件下本发明算法可以识别更多的目标，或者说本发明算法在相同的阵列配置下，支持更低的快拍数目。由于本发明算法在最终估计dod与doa时无法采用ls方法，因此相对现有文献中的parafac算法，所提算法有孔径损失，最终估计精度可能劣于parafac算法。但本发明算法可应对相干源场景，而现有文献中的parafac算法对相干源并不适用。

为具体对本发明的效果进行说明，本发明采用蒙特卡洛手段对所提算法的有效性进行验证。仿真中假设k＝3个点目标处于雷达收发阵列远场，其doa和dod分别为和其多普勒频率分别为200，400和850hz。目标在l＝100个cpi内的雷达截面系数满足swerlingi模型。mimo雷达配置有m＝12个发射阵元和n＝10个接收阵元。发射的基带编码波形为hm表示由q×q维的哈达码矩阵的前m行构成。一个cpi内的编码码长为q＝128，脉冲重复频率为20khz。本发明所模拟的互耦仿真场景有两个，分别是

场景一：收发阵元弱互耦干扰背景，p＝1，互耦系数分别为ct＝[1,0.1174+j0.0577]，cr＝[1,-0.0121-j0.1029]；

场景二：收发阵元强互耦干扰背景，p＝2，互耦系数分别为ct＝[1,0.8+j0.5,0.2+j0.1]，cr＝[1,0.6+j0.4,0.1-j0.3]。

附图2是在snr＝-15db、场景一、非相干源条件下本发明算法进行200次蒙特卡洛仿真的散点图，附图3是在snr＝-10db、场景二、相干源(目标一和目标二的相干度为0.99)条件下本发明算法200次蒙特卡洛实验的散点图。可以看出，两种仿真条件下三个目标的可以清楚的被估计出来，并且被正确配对，因而本算法对非相干源和相干源均适用。

为进一步比较本发明算法与其它算法性能，将所有算法进行200次独立的蒙特卡洛仿真，所对比的算法有esprit算法0、hosvd算法0和parafac算法0。仿真中的信噪比定义为联合dod与doa估计的精度采用归一化均方根误差(regularizedmeansquarederror，rmse)和成功检测概率(probabilityofthesuccessfuldetection，psd)两种标准评价。其中，rmse定义为

式中，分别为第i次蒙特卡洛仿真中获得的对θk与的估计。psd定义为成功检测的次数占总实验次数的百分比，其中，若所有估计角度的绝对误差之和小于0.5°，则定义该次仿真成功检测。

附图4与附图5分别为所有算法在场景一、非相干源、不同信噪比条件下所提算法rmse和psd性能的对比。由图4可知，在低信噪条件下，张量算法性能较为接近，但性能均优于esprit算法。随着信噪比增加，所有算法的性能均有所提高，但本发明算法在信噪比较低时性能优于hosvd算法，在高信噪比条件下性能接近hosvd。同时，所提算法性能会劣于parafac，这是由本发明算法在最后估计过程中存在孔径损失造成的。由附图5可知，所有算法的psd在高信噪比时都会达到100％。随着信噪比的降低，psd会下降，其开始下降所对应的信噪比位置被称为信噪比阈值。可以看出，但使用了张量计算的算法信噪比阈值要低于esprit。此外，所提算法的psd性能在信噪比低于阈值时优于hosvd但劣于parafac。

附图6与附图7分别为所有算法在场景二、非相干源、不同信噪比条件下所提算法rmse和psd性能的对比。对比附图4、5中的相关曲线可知，强互耦环境下相关算法的性能均有所下降。但是本发明算法的rmse性能与psd性能仍处于hosvd与parafac之间，但仍然远优于esprit算法。考虑到本发明所提算法在计算复杂度方面具有很大的优势，因而本发明所提算法可获得估计精度和估计复杂度方面的折衷。

附图8与附图9分别为所有算法在在场景二、相干源、不同信噪比条件下所提算法rmse和psd性能的对比，其中第一个目标和第二个目标的相干度为0.99。可以看出，esprit算法和parafac算法均不能有效的分辨出相干源，而hosvd算法和本发明算法此时均能够有效工作。此外，本发明算法在低信噪比条件下性能优于hosvd算法，在高信噪比条件下性能与hosvd方法非常接近。综合考虑到本发明算法的复杂度低于hosvd方法，本发明算法要优于hosvd方法。

本发明所述互耦条件下双基地mimo雷达角度估算方法，其利用阵列信号的多维结构，将匹配滤波后的雷达数据表述成一个三阶张量模型。考虑到均匀线性阵列互耦矩阵的带状toeplitz特性，利用部分阵元方向矩阵具有共同的尺度变换特性消除互耦的影响。结合前后平滑技术和酉变换技术，构建去耦后数据的增广输出三线性模型，再将联合dod与doa估计与三线性模型相联系。最后，通过最小二乘方法估计目标的dod与doa。所述互耦条件下双基地mimo雷达角度估算方法，其与传统算法相比，能有效应对收发阵列存在互耦的场景，无需额外的校准源、奇异值分解以及谱峰搜索；还能够自动匹配所估计的dod与doa；且通过采用三线性分解仅涉及实数运算，降低计算复杂度；同时对相干源仍然适用。

以上所述仅为本发明的较佳实施例，并不用以限制本发明，凡在本发明的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。