一种基于太阳震荡时间延迟的自主天文导航方法与流程

本发明属于航天器自主导航领域，涉及一种利用太阳震荡引起的光谱波长变化作为特征提供航天器位置信息的天文导航方法，适用于太阳系内行星探测转移轨道或环绕轨道的导航定位。

背景技术：

对于深空探测任务而言，航天器的制导与控制需要依赖导航信息，导航精度对于任务的成败有着重要影响。导航即获得航天器的位置及速度信息，确定轨道参数。

目前，一般通过地面测控站为航天器提供导航信息。然而，随着航天器与地球之间距离的增加，信号传输的双程时延将越来越大。另外，日凌将造成信号中断。随着航天器数目不断增加，成本和资源等方面也受到限制。

天文导航是一种自主导航方法，能够通过观测天体信息获得实时准确的导航信息。目前常用的天文导航方法包括测角导航、基于x射线脉冲星测距导航和天文多普勒测速导航。测角导航是一种传统、成熟的天文导航方法，通过测量航天器与近天体及导航恒星之间的夹角获得航天器的位置信息。但是，这种方法的导航精度随着航天器与近天体间距离的增加而下降。基于x射线脉冲星测距导航可以提供高精度的位置信息，且导航精度不受航天器与天体间位置的影响。但是，由于x射线脉冲星的信号比较微弱，通常需要通过较长时间的历元折叠以得到量测量。天文多普勒测速导航通过测量由航天器与恒星间径向运动造成的光谱频移获得航天器的速度信息。但是，这种方法无法提供位置信息，且恒星光谱的动态变化将影响其导航精度。

技术实现要素：

本发明要解决的技术问题是：为弥补现有天文导航方法的不足，提出一种利用太阳震荡造成的波长变化特征提供航天器导航信息的时间延迟量测量，并提出一种包含二分法的隐式无迹卡尔曼滤波解决量测模型是隐式且含有非线性方程的问题，为转移轨道或环绕轨道的航天器提供实时、高精度的自主导航信息。

本发明解决其技术问题所采用的技术方案为：以太阳震荡引起的太阳光谱线心波长变化为特征，获得太阳震荡时间延迟量测量；建立航天器的状态模型及时间延迟量测模型，使用包含二分法的隐式无迹卡尔曼滤波估计航天器的导航参数。

具体包括以下步骤：

1.获取太阳震荡时间延迟量测量

利用原子鉴频仪检测光谱线心波长的变化。第一原子鉴频仪朝向太阳安装，测量直接观测太阳光的线心波长，并标记时间。同时，第二原子鉴频仪朝向反射天体安装，测量经反射太阳光的线心波长，并标记时间。由于航天器与太阳或反射天体之间的相对运动，会引起光谱的多普勒频移。考虑到它们之间的相对径向速度的变化是缓慢呈趋势的，因此可以通过平滑获得其长期趋势，并获得仅反映太阳震荡的去趋势的线心波长。由于太阳光的传播路径不同，太阳光谱线心波长的变化将先后被两个原子鉴频仪记录。太阳震荡引起的波长变化特征被第二原子鉴频仪在t时刻记录，通过特征匹配确定此特征被第一原子鉴频仪记录的时刻t1。可得到太阳震荡时间延迟量测量如下：

z＝[△t]＝[t-t1](1)其中z是选取的量测量，△t是时刻t及t1间的时间延迟。

2.建立基于轨道动力学的天文导航系统状态模型

用以太阳为中心天体的受摄三体模型描述航天器的运动，将其他扰动视为过程噪声。在太阳中心惯性坐标系(j2000.0)下的动力学模型可写为：

其中|·|表示矢量的2范数，r和v是航天器相对太阳的位置和速度。μs和μm分别是太阳和火星的引力常数，rm是火星相对太阳的位置矢量，rsm＝r-rm是航天器相对火星的位置矢量。wv是各种扰动造成的过程噪声。可由上式得到状态模型如下：

其中状态量x＝[r,v]^t为航天器在太阳惯性坐标系下的位置及速度，为状态量x的导数，为时刻t的f(x,t)为系统非线性连续状态转移函数，w为过程噪声，w(t)为时刻t的w。

3.建立太阳震荡时间延迟的量测模型

太阳震荡在t0时刻发生，此时航天器的位置及速度分别是r0和v0，反射天体的位置及速度分别是rr0和vr0。第一原子鉴频仪在t1时刻记录此震荡引起的线心波长变化，此时航天器的位置及速度分别是r1和v1，反射天体的位置及速度分别是rr1和vr1。太阳光在tr时刻被反射天体反射，此时反射天体的位置及速度分别是rrr和vrr。第二原子鉴频仪在t时刻记录此震荡引起的线心波长变化，此时航天器的位置及速度分别是r和v。

通过轨道动力学由r和v求出r1和v1：

(r1,v1)＝f′(r,v,△t)(4)

其中，f′(·)表示f(·)的逆过程。

通过t1和r1求出t0：

其中c表示光速。由于：

c·(tr-t0)＝|rrr|(6)

且

(rrr,vrr)＝f(rr1,vr1,tr-t1)(7)

用二分法解上述非线性方程，求出tr，并得到rrr。

通过r1及rrr，建立太阳震荡时间延迟的隐式量测模型：

(|rrr|+|r-rrr|-|r1|)/c-△t＝0(8)

其中rrr是r1的函数，而r1又是r、v及△t的函数。考虑量测误差，隐式量测模型如下表示：

0＝h(x,z-v)(9)

其中v是太阳震荡时间延迟测量误差。

4.在没有太阳震荡时间延迟量测量时，以固定滤波周期通过步骤2的状态模型进行时间更新获得状态估计及误差协方差估计。当获得太阳震荡时间延迟量测量时，在时间更新后进行量测更新，结合步骤2和步骤3所述的状态模型及量测模型，通过包含二分法的隐式无迹卡尔曼滤波获得状态估计及误差协方差估计，得到导航信息，并将这些导航信息分别返回滤波器，用于估计下一时刻航天器的导航信息。

本发明的原理是：利用太阳震荡引起的太阳光谱线心波长的剧烈变化作为特征，分别通过一个朝向太阳安装直接观测太阳光的原子鉴频仪及一个朝向反射天体(如火星、火星卫星、小行星)安装观测反射太阳光的原子鉴频仪，观测太阳光谱波长的变化，记录变化发生时刻，得到沿两种路线传播的太阳光线的时间延迟。由于时间延迟与太阳、反射天体及航天器的位置有关，因此可以作为量测量提供航天器的位置信息。根据轨道动力学建立航天器的状态模型，根据各天体间位置关系及运动规律建立含有非线性方程的太阳震荡时间延迟隐式量测模型，通过包含二分法的隐式无迹卡尔曼滤波实现对航天器位置、速度等导航参数的估计。

本发明与现有技术相比的优点在于：(1)可利用现有的原子鉴频仪对太阳光谱波长进行观测获取量测量，而不需要专门研制新的探测器。(2)仅需两个光电探测器即可达到较高的导航结果，而不需要观测三颗恒星或观测三颗脉冲星以达到收敛结果，节约了空间及成本。(3)在原子鉴频仪时间分辨率较高的情况下，可提供高精度的导航信息。

附图说明

图1为本发明中获取太阳震荡时间延迟量测量的示意图；

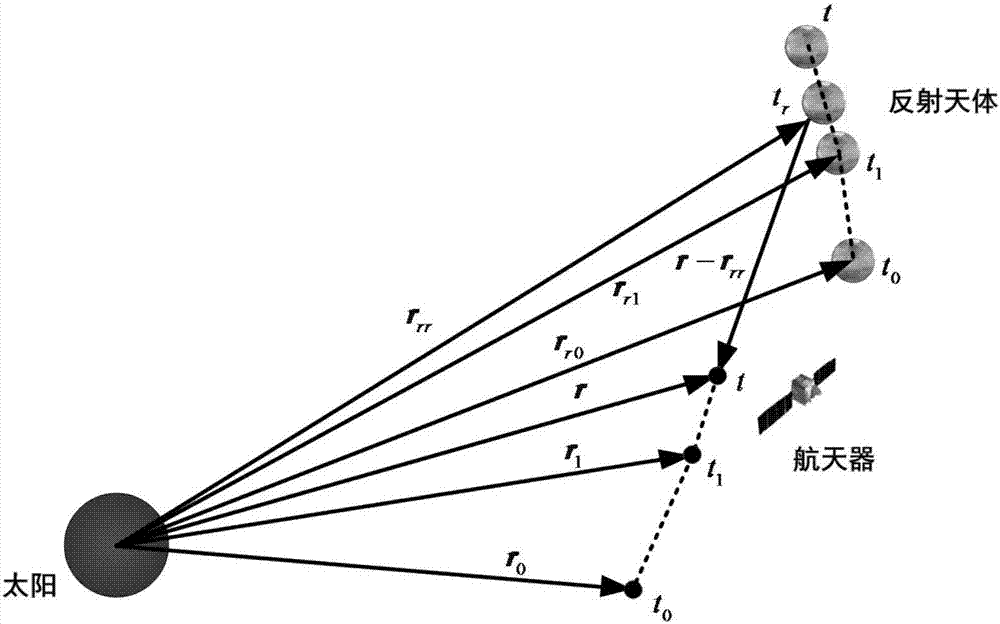
图2为本发明中的航天器与天体之间位置关系示意图；

图3为本发明中的包含二分法的隐式无迹卡尔曼滤波流程图。

具体实施方式

本发明通过观测直接接收的太阳光谱波长及经天体反射的太阳光谱波长获得航天器的导航信息，因此可适用于太阳系内任何行星探测转移轨道或环绕轨道的导航定位。这里以火星探测转移轨道为例，以火卫一作为反射天体，说明本发明的具体实施过程：

1.获取太阳震荡时间延迟量测量

如图1所示，利用两个原子鉴频仪分别检测沿不同路径传播的太阳光谱线心波长的变化，其中第一原子鉴频仪朝向太阳安装，测量直接观测太阳光的线心波长，并标记时间；第二原子鉴频仪朝向反射天体安装，测量经反射太阳光的线心波长，并标记时间。由于航天器与太阳或反射天体之间的相对运动会引起光谱的多普勒频移，因此得到的原始的太阳光谱线心波长变化不仅包含太阳震荡的影响，还包含相对运动的影响。考虑到它们之间的相对径向速度的变化是缓慢呈趋势的，因此通过平滑获得其长期趋势，然后获得仅反映太阳震荡的去趋势的线心波长。由于太阳光的传播路径不同，太阳光谱线心波长的变化将先后被两个原子鉴频仪记录。第二原子鉴频仪记录太阳震荡引起的波长变化特征得到t，通过特征匹配确定此特征被第一原子鉴频仪记录的时刻得到t1。由此可得到太阳震荡时间延迟量测量如下：

z＝[△t]＝[t-t1](10)

其中z是选取的量测量，△t是时刻t及t1间的时间延迟。

2.建立基于轨道动力学的天文导航系统状态模型

用以太阳为中心天体的受摄三体模型描述航天器的运动，将其他扰动视为过程噪声。在太阳中心惯性坐标系(j2000.0)下的动力学模型可写为：

其中|·|表示矢量的2范数，r和v是航天器相对太阳的位置和速度。μs和μm分别是太阳和火星的引力常数，rm是火星相对太阳的位置矢量，rsm＝r-rm是航天器相对火星的位置矢量。wv是各种扰动造成的过程噪声。可由上式得到状态模型如下：

其中状态量x＝[r,v]^t为航天器在太阳惯性坐标系下的位置及速度，为状态量x的导数，为时刻t的f(x,t)为系统非线性连续状态转移函数，w为过程噪声，w(t)为时刻t的w。

3.建立太阳震荡时间延迟的量测模型

航天器与天体之间位置关系如图2所示。太阳震荡在t0时刻发生，此时航天器的位置及速度分别是r0和v0，反射天体的位置及速度分别是rr0和vr0。太阳震荡引起的线心波长变化在t1时刻被安装在航天器上的第一原子鉴频仪记录，此时航天器的位置及速度分别是r1和v1，反射天体的位置及速度分别是rr1和vr1。太阳光在tr时刻被反射天体反射，此时反射天体的位置及速度分别是rrr和vrr。此震荡引起的线心波长变化在t时刻被安装在航天器上的第二原子鉴频仪记录，此时航天器的位置及速度分别是r和v。

通过轨道动力学由r和v求出r1和v1：

(r1,v1)＝f′(r,v,△t)(13)

其中，f′(·)表示f(·)的逆过程。

通过t1和r1求出t0：

其中c表示光速。由于：

c·(tr-t0)＝|rrr|(15)

且

(rrr,vrr)＝f(rr1,vr1,tr-t1)(16)

用二分法解上述非线性方程，求出tr，并得到rrr。

通过r1及rrr，建立太阳震荡时间延迟的隐式量测模型：

(|rrr|+|r-rrr|-|r1|)/c-△t＝0(17)

其中rrr是r1的函数，而r1又是r、v及△t的函数。考虑量测误差，隐式量测模型可如下表示：

0＝h(x,z-v)(18)

其中v是太阳震荡时间延迟测量误差，h(·)表示量测函数。

4.通过滤波获得航天器状态估计

包含二分法的隐式无迹卡尔曼滤波流程如图3所示。在没有太阳震荡时间延迟量测量时，以固定滤波周期t通过步骤2的状态模型进行时间更新获得状态估计及误差协方差估计。具体步骤为：

①初始化状态量和状态误差方差阵p0

式中，是第0时刻(初始时刻)航天器位置及速度的估计值，x0是第0时刻航天器位置及速度的真实值。

②选取sigma采样点

在附近选取一系列采样点，这些样本点的均值和协方差分别为和状态变量为6×1维，那么选取13个样本点及其权重w0,w1…,w12分别如下：

其中τ表示缩放参数，表示取平方根矩阵的第i行或列。

③传递sigma采样点并获得先验估计及先验误差协方差

每个采样点的一步预测为：

合并所有获得先验状态估计为：

先验误差协方差为

式中，qk为k时刻状态模型噪声协方差阵。

当获得太阳震荡时间延迟量测量时，在时间更新后继续进行量测更新，结合步骤2和步骤3所述的状态模型及量测模型，通过包含二分法的隐式无迹卡尔曼滤波获得状态估计及误差协方差估计，得到导航信息。具体步骤为：

④构造量测方程

首先通过式(4)得到r1和v1，通过式(5)得到t0后，由式(6)及式(7)构造关于tr的非线性方程，使用二分法解此方程得到tr，通过tr及式(7)得到rrr。由r1及rrr可建立隐式量测方程(式(8))。

⑤计算预测量测噪声协方差

首先在时间延迟量测量zk附近选取一系列样本点，这些样本点的均值和协方差分别为zk和rk。量测量为1维，因此选取3个样本点及其权重w0,w1,w2分别如下：

通过步骤④得到的量测方程，计算每个采样点的预测量测量为：

合并所有获得预测量测sk为：

预测量测噪声协方差tk为：

⑥量测更新

通过步骤④得到的量测方程，计算每个采样点的预测量测量为：

合并所有获得预测量测yk为：

通过步骤⑤得到的预测量测噪声协方差tk，计算预测量测协方差及互协方差：

计算滤波增益kk为：

计算后验状态估计

计算后验误差协方差

将获得的状态量的估计值和估计协方差输出，其中状态估计值包括航天器的位置、速度信息，输出的状态估计方差pk表示了滤波估计的性能，同时将这些估计值返回滤波器，用于获得k+1时刻的输出。

本发明说明书中未作详细描述的内容属于本领域专业技术人员公知的现有技术。