基于反卷积的自给能中子探测器延迟效应消除方法与流程

本发明属于中子探测技术领域，具体涉及一种基于反卷积的自给能中子探测器延迟效应消除方法。

背景技术：

核能因为能量密度高，在可持续能源结构中占有不可替代的地位。但是核安全是核能应用中必须解决的关键问题。在核反应堆中，中子通量密度是监测和控制反应堆正常运行的关键物理量。由于反应堆堆芯是高温高压和强辐照环境，一般的探测器难以胜任。而自给能探测器由于具有不需偏压、结构简单、体积小、全体固化、电子学设备简单等特性，成为监控反应堆堆芯中子通量的重要探测器。目前应用较多的自给能探测器主要有⁵⁹co探测器、¹⁰³rh探测器、⁵¹v探测器等。自给能探测器的探测原理如下：探测器在堆芯中吸收中子后会经过多种途径放出电子，当电子被收集电极收集时将会在回路中产生电流，此电流强度与堆内中子通量密度有相关关系，所以通过测量这一电流强度可以达到测量反应堆中中子通量的目的。但是，自给能中子探测器的电流信号受到中间不稳定核素半衰期的限制，在反映中子通量密度的变化上存在延迟，影响了该探测器在反应堆实时安全保护系统中的应用。

针对上述问题，本项目提出了一种消除自给能中子探测器延迟效应的方法，能够把延迟效应降低到1秒之内，能够大大提高反应堆的安全性。

国内外的学者对自给能探测器的延迟修正方法有过很多的研究，固然成果不少，但往往涉及拉普拉斯变换、z变换，较为复杂，难于理解。

技术实现要素：

为了克服上述现有技术存在的问题，本发明的目的在于提供一种基于反卷积的自给能中子探测器延迟效应消除方法，具有容易理解，精度高的优点。

为了达到上述目的，本发明采用如下技术方案：

基于反卷积的自给能中子探测器延迟效应消除方法，其详细步骤如下：

步骤1：根据探测器材料在中子场中的反应物理过程画出其反应机制原理图；

步骤2：根据步骤1画出的反应机制原理图给出的各元素生成及衰变关系写出探测器单位体积内各中间核素数量ni(t)关于中子通量密度φ(t)的动态微分方程组(1)，写出探测电流i(t)与各中间核素数量及中子通量密度φ(t)的表达式(2)；

式中：i表示第i个相关核素，取值为0到m；

j表示第j个相关元素，取值为0到j‐1；

m表示共有m个相关核素；

t表示时间；

σi为在探测器单位体积内反应生成第i个相关核素的宏观截面；

fi为探测器内产生第i个相关核素时产生瞬时电流的效率；

ji为探测器内的第i个相关核素退激或衰变时的电流产生效率；

λi为第i个相关核素的衰变常数；

λj为第j个相关核素的衰变常数；

ni(t)为第i个相关核素单位体积内核素数量；

nj(t)为第j个相关核素单位体积内核素数量；

步骤3：将中子通量密度φ(t)假设为单位脉冲信号δ(t)，见表达式(3)，具体推导出探测器单位体积内各中间核素数量ni(t)的表达式(4)及探测电流i(t)与时间t的表达式(5)，那么，以单位脉冲信号输入产生响应的探测电流即为探测器的单位冲激响应(6)；

式中：i表示第i个相关核素；t表示时间；

∑i为在探测器单位体积内反应生成第i个相关核素的宏观截面；

ni(t)为第i个相关核素单位体积内核素数量；

λi为第i个相关核素的衰变常数；

h(t)为探测器的单位冲激响应；

ai和bi参数因子由具体探测器材料给出；

步骤4：对于一般的中子通量密度φ(t)，探测电流i(t)就有关系式(7)，由于探测电流是连续的，所以对中子探测器实际测量的电流值进行采样，得到电流的取样值i(nδt)；

卷积表达式为：

i(t)＝φ(t)*h(t)(7)

步骤5：将步骤4得到的卷积关系式(7)离散化，对一个单位冲激响应为h(t)的线性时不变因果系统，即在自给能中子探测器系统中，输入信号函数与输出信号函数之间的关系可以用卷积表示为(8)式，离散化后具体表示为(12)式。具体如下所述：

离散化处理后卷积表达式为：

i(n)＝φ(n)*h(n)(8)

i(n)为第n个采样点的电流值；

φ(n)为第n个采样点的中子通量密度；

h(n)为第n个采样点的单位冲激响应；

其中：

i(n)＝i(nδt)(9)

δt为采样时间间隔；

i(n)为第n个采样点的电流值用第n个时间点的电流值i(nδt)表示；

φ(n)＝φ(nδt)(10)

δt为采样时间间隔；

φ(n)为第n个采样点的中子通量密度用第n个时间点的中子通量密度φ(nδt)表示；

显然，此处：

离散化处理后电流表达式为：

设那么离散化处理后电流表示为：

其中结合(11)式的积分结果可得：

联立(13)、(14)式可得迭代式：

其中：

s为探测器对中子的瞬时成分的灵敏度；

σi为在探测器内反应生成第i个相关核素的总截面；

fi为探测器单位体积内产生第i个相关核素时产生瞬时电流的效率；

ii(n)为第i种缓发电流在第n个采样点的电流值；

ii(n+1)为第i种缓发电流在第n+1个采样点的电流值；

hi(n)为第i种缓发电流在第n个采样点的单位冲激响应；

步骤6：确定计算中子通量的迭代关系式，首先根据i(n)的表达式列出方程，再列出i(n+1)的方程，看两者的迭代关系，再由i(n+1)式中导出中子通量密度φ(n+1)的表达式；

具体过程如下：

由式(13)得到：

其中：

φ(n)为第n个采样点的中子通量密度；

i表示第i个相关核素，取值为0到m(m为相关核素的总数)；

ii(n+1)为第i种缓发电流在第n+1个采样点的电流值；

结合式(15)、(16)可知，由当前时段的所有缓发电流成分，中子通量密度和当前所测得的电流就可得出下一时间点的中子通量密度值；

步骤7：确定迭代式的初值，根据电流信号的是否发生突变来判断中子通量是否发生突变，若是电流信号平稳，那么取前m+1个采样点，即在(m+1)δt的采样时间内，列出假设中子通量密度不发生变化的齐次线性方程组，解这个方程组便可以得到带入迭代式的初始值；若电流信号发生突变，说明中子通量密度此时刻不稳定，那么，处理方法为将向后延迟几秒取若干个点，列出齐次线性方程组求解得到迭代式初始值；

具体过程如下：

列出关于初值的矩阵并由cramer法则求解：

步骤8：迭代得到中子通量密度，将步骤7中得到的初值带入下列迭代式中，便能够由当前时间的所有缓发电流成分、中子通量密度和当前所测得的电流就可得出下一时间点的中子通量密度值；

其中：

δt为采样时间间隔；

i表示第i个相关核素，取值为0到m(m为相关核素的总数)；

ii(n)为第i种缓发电流在第n个采样点的电流值；

ii(n+1)为第i种缓发电流在第n+1个采样点的电流值；

λi为第i个相关核素的衰变常数；

φ(n)为第n个采样点的中子通量密度；

φ(n+1)为第n+1个采样点的中子通量密度；

hi(1)为第i种缓发电流在第1个采样点的单位冲激响应；

与现有技术相比，本发明具有如下优点：

步骤2中影响电流信号延迟的原因考虑周全，不仅有中间核素发生的衰变过程，还包括不稳定核素的退激过程，不会因为忽略小电流是的消除延迟效应的结果产生较大误差。

步骤3‐步骤6均为简单的数学处理及迭代过程，相对于进行拉普拉斯变换以及z变换处理，过程简单易操作。

步骤7考虑了进行迭代时初值的选取，在探测器刚开始工作时，初值可以选择为缓发电流成分值为0，瞬发电流成分可依据公式求出，在探测器已测量电流一段时间后，迭代的初值由方程组确定。

附图说明

图1为本发明流程示意图。

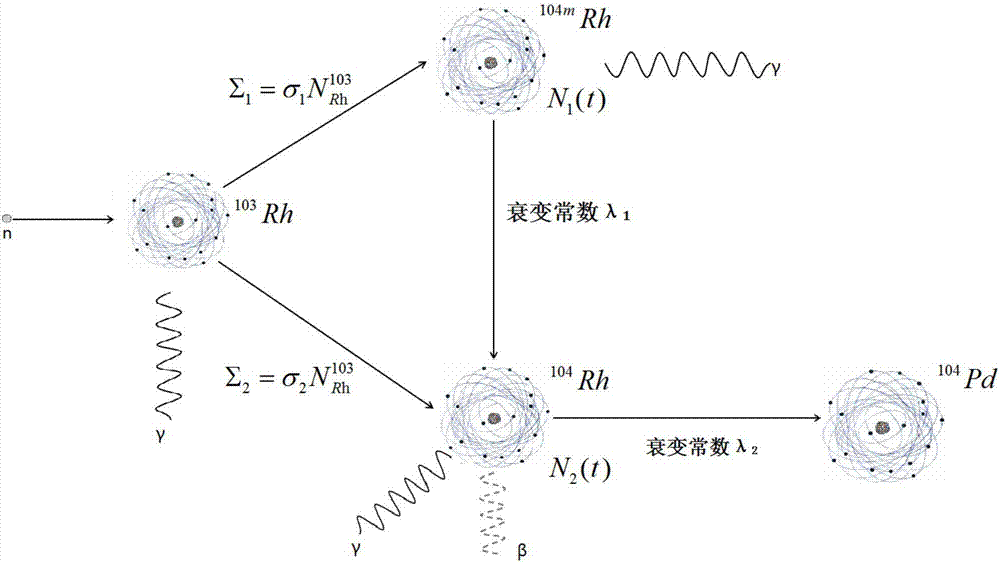
图2为探测器探测中子相关反应过程图。

图3为输入为矩形信号形式中子通量密度的延迟效应修正效果图。

图4为在电流发生突变时，延迟效应的修正效果图。

图5为在探测电流的某一时刻开始延迟修正的效果图。

图6为输入为三角信号形式中子通量密度的延迟效应修正效果图。

具体实施方式

以下结合附图及具体实施例，对本发明作进一步的详细描述。

目前在反应堆内的自给能中子探测器有很多种，其中铑自给能中子探测器的反应机理最为复杂，缓发电流成分较多，半衰期长。所以，为验证本专利的可靠性、合理性，我们以铑自给能中子探测器为例进行详细说明：

具体方法过程如图1所示。

步骤1：根据探测器材料¹⁰³rh在中子场中的反应物理过程画出其反应机制原理图，如图2所示。

步骤2：根据图2将公式(1)具体化写出探测器单位体积内^104mrh的个数n1(t)及¹⁰⁴rh的个数n2(t)关于中子通量密度φ(t)的动态微分方程(1‐1)和(1‐2)，并将公式(2)具体化写出探测电流i(t)与n1(t)、n2(t)及中子通量密度φ(t)的表达式(2‐1)。

其中：

为探测器单位体积内¹⁰³rh核素的个数；

n1(t)为探测器单位体积内^104mrh的个数；

n2(t)为探测器单位体积内¹⁰⁴rh的个数；

σ1为¹⁰³rh与中子反应生成^104mrh的微观反应截面；

σ2为¹⁰³rh与中子反应生成¹⁰⁴rh的微观反应截面；

λ1为^104mrh的衰变常数；

λ2为¹⁰⁴rh的衰变常数；

f1与f2分别为探测器内产生(n,γ)反应生成^104mrh和¹⁰⁴rh时产生的伽马射线转化为瞬时电流的效率；

为探测器对中子的瞬时成分的灵敏度；

j1为探测器内的^104mrh退激成¹⁰⁴rh放出的γ射线与物质产生探测器电流的效率；

j2为探测器内的¹⁰⁴rhβ衰变产生电流的效率；

φ(t)为中子通量密度；

i(t)为探测电流；

步骤3：将中子通量密度φ(t)假设为单位脉冲信号δ(t)，见表达式(3)，具体由公式(4)推导出探测器单位体积内各中间核素数量ni(t)的表达式(4‐1)、(4‐2)及探测电流i(t)将公式(5)具体化写作与时间t的表达式(5‐1)，那么，以单位脉冲信号输入产生响应的探测电流即为探测器的单位冲激响应，即将一般形式的公式(6)写作表达式(6‐1)；

那么，冲激响应：

写作

其中：

为探测器单位体积内产生(n,γ)反应生成^104mrh的宏观截面；

为探测器单位体积内产生(n,γ)反应生成¹⁰⁴rh的宏观截面；n1(t)为探测器单位体积内^104mrh的个数；

n2(t)为探测器单位体积内¹⁰⁴rh的个数；

λ1为^104mrh的衰变常数；

λ2为¹⁰⁴rh的衰变常数；

f1与f2分别为探测器内产生(n,γ)反应生成^104mrh和¹⁰⁴rh时产生的伽马射线转化为瞬时电流的效率；

为探测器对中子的瞬时成分的灵敏度；

j1为探测器内的^104mrh退激成¹⁰⁴rh放出的γ射线与物质产生探测器电流的效率；

j2为探测器内的¹⁰⁴rhβ衰变产生电流的效率；

φ(t)为中子通量密度；

i(t)为探测电流；

步骤4：对于稳定的中子通量密度φ(t)，探测电流i(t)有关系式。

i(t)＝φ(t)*h(t)(7)

由于电流信号是连续的，所以对中子探测器实际测量的电流值进行采样，使取样间隔恒定为δt，得到电流的取样值i(nδt)；

步骤5：将步骤4得到的探测电流i(t)卷积关系式离散化，对一个单位冲激响应为h(t)的线性时不变因果系统，即在自给能中子探测器系统中，输入信号函数与输出信号函数之间的关系可以用卷积表示为(8)式；

具体过程为：

设

那么，可知：

i(n)＝φ(n)*h(n)

由公式(11)得到具体形式(11‐1)、(11‐2)、(11‐3)

并且，结合(11‐1)、(11‐2)式和假设将公式(14)具体化得到：

其中：

h1(n)，h2(n)为缓发电流成分对应的冲激响应离散化部分；

步骤6：确定计算中子通量的迭代关系式，首先根据i(n)的表达式列出方程，再列出i(n+1)的方程，看两者的迭代关系，再由i(n+1)式中导出中子通量密度φ(n+1)的表达式；

具体过程：由卷积表达式(8)和步骤5离散化后将公式(12)具体化可得电流响应为(12‐1)、(12‐2)、(12‐3)：

s＝f1σ1+f2σ2

那么，设

其中由式(15)具体化可得(15‐1)、(15‐2)：

由上式可得，中子通量密度迭代式(16)可改写为(16‐1)：

其中：

ii(n),i＝1,2，为第i种缓发电流成分；

为探测器对中子的瞬时成分的灵敏度；

所以只要知道当前时间的所有缓发电流成分，中子通量密度和当前所测得的电流就可得出下一时间点的中子通量密度值。

步骤7：确定迭代式的初值，根据电流信号的是否发生突变来判断中子通量是否发生突变，若是电流信号平稳，那么取前前m+1个采样点，即在(m+1)δt的采样时间内，列出假设中子通量密度不发生变化的齐次线性方程组，解这个方程组便可以得到带入迭代式的初始值。若是电流信号发生突变，说明中子通量密度此时刻不稳定，那么，处理方法为将向后延迟几秒取若干个点，列出齐次线性方程组求解得到迭代式初始值；

具体过程：首先，对实际测量的电流信号曲线进行判断，若是电流信号发生突变，那么取电流曲线上延后几秒处的几个采样点来列出方程进行求解。若是电流信号平稳，那么取前几个点确定初值，这里取前三个点。由于不管电流信号是否突变，都是进行求解齐次线性方程来获得初值，这里就假设电流信号平稳来说明此方法。

采样点的电流大小满足关系式(13)、将(13)具体到采样点可得:

(13‐1)式由关系式(14)、(15)可具体写为：

即：

由此，设行列式：

那么，由cramer法则可以得到迭代式初始值的解为：

步骤8：将步骤7中得到的初始值带入下列迭代式中，便可以由当前时段的所有缓发电流成分，中子通量密度和当前所测得的电流就可得出下一时间段的中子通量密度值；

取值说明：

^104mrh的半衰期为258.0秒，则^104mrh的衰变常数

¹⁰⁴rh的半衰期为42.4秒；则¹⁰⁴rh的衰变常数

¹⁰³rh与中子反应生成^104mrh的微观反应截面σ1＝1.1×10^‐23cm²；

¹⁰³rh与中子反应生成¹⁰⁴rh的微观反应截面σ2＝1.35×10^‐22cm²。

由于所考察的时间长度远小于探测器的寿命长度，所以假设在考察时间段内探测器单位体积内¹⁰³rh核素的个数保持不变，即为常数；由于铑的密度为12.7g/cm³,则单位体积内含有¹⁰³rh的个数

这里ρ＝12.7g/cm³为铑的密度；

m＝103g/mol为铑的摩尔质量，na＝6.02×10²³mol^‐1为阿伏伽德罗常数。则探测器单位体积内产生(n,γ)反应生成^104mrh以及¹⁰⁴rh的宏观截面分别为

铑自给能中子探测器的中子的灵敏度典型值为3.6×10^‐20

a/(cm²·s)，其中瞬时成分占比约为5％～15％，此处取10％，即

j1与j2的值将在实际应用过程中根据探测器刻度值进行调谐确定；在这里暂且取j1＝2.9897×

10^‐22a/(cm³*s),j2＝2.989710^‐21a/(cm³*s)；采样步长ts可以根据具体情况进行优化，这里暂取为0.1秒。

应用实例：

为了突出消除时间延迟的效果，考查将铑探测器突然放入一个稳定的中子场的过程，通常认为延迟时间是达到稳态值的95％所需的时间。以反应堆启堆过程为例，模拟反应堆中中子通量密度φ＝0(cm²·s)^‐1在t＝100秒时到突然变为φ＝5×10¹³(cm²·s)^‐1的过程；整个过程前100秒中子通量密度φ＝0(cm²·s)^‐1，在第100秒时中子通量密度突变为φ＝5×10¹³(cm²·s)^‐1，并一直维持。在此模拟过程中，各相关参数参照具体实施方式以及取值说明部分中所述情形进行取值，电流取样时间步长ts＝0.1秒。

消除延迟效应的结果如图3、4所示，包括归一化中子通量密度和归一化电流随时间变化的曲线。归一化中子通量密度为用消除延迟算法得出的中子通量密度与突变后中子通量密度的比值(归一化分母取5×10¹³(cm²·s)^‐1)；在图3中可以看出电流需要几百秒时间才能达到稳定，即如果仅仅依据电流数据来显示中子通量密度的话将存在很大的延迟，如果采用这种方法的话，对反应堆中子通量密度的监控也失去了意义；与之相对，采用消除延迟算法得出来的中子通量密度与实际中子通量密度吻合得非常好，同时将图3前端放大提取为图4，在图4中可以看出延迟在理想情况下完全被消除，可以实现了反应堆中子通量密度的实时监控，更利于反应堆安全控制。为了验证本方法的正确性，如图6所示，对于三角形式的中子通量密度曲线也能很好的修正延迟效应，实现实时中子通量密度值的监控。

不仅可以从起始阶段开始修正延迟效应，根据本专利中的迭代初值确定方法，可以从任意时刻开始修正延迟，修正效果好，如图5所示，从中间时段开始修正，延迟效应能被很好地消除。

虽然已参照典型实施例描述了本发明，但应该理解，所用的术语是说明和示例性、而非限制性的术语。由于本发明能够以多种形式具体实施而不脱离发明的精神和实质，所以应当理解，上述实施例不限于任何前述的细节，而应该在随附权利要求所限定的精神和范围内广泛地解释，因此落入权利要求或其等效范围内的全部变化和改型都应为随附权利要求所覆盖。