一种基于最小二乘定位的不确定性分析方法与流程

本发明涉及无线定位技术。

背景技术：

实际无线通信环境中，由于噪声、环境和测量误差等不良因素的影响，引起通信距离估计具有较大的误差，导致最小二乘定位结果具有很强的不确定性，给定位结果在导航等后续应用处理方法提出了挑战。本发明针对上述问题，对最小二乘定位过程中的不确定性的因素进行敏感性分析，分析出导致不确定性的主要因素及其对定位计算结果的影响程度，并对定位计算结果的不确定性进行评估，为改善无线定位精度方法提供指导。

技术实现要素：

本发明的目的是为了解决最小二乘定位计算过程中的不确定性敏感性分析和不确定性综合问题，提供一种基于最小二乘定位的不确定性分析方法。

本发明所述的一种基于最小二乘定位的不确定性分析方法包括以下步骤：

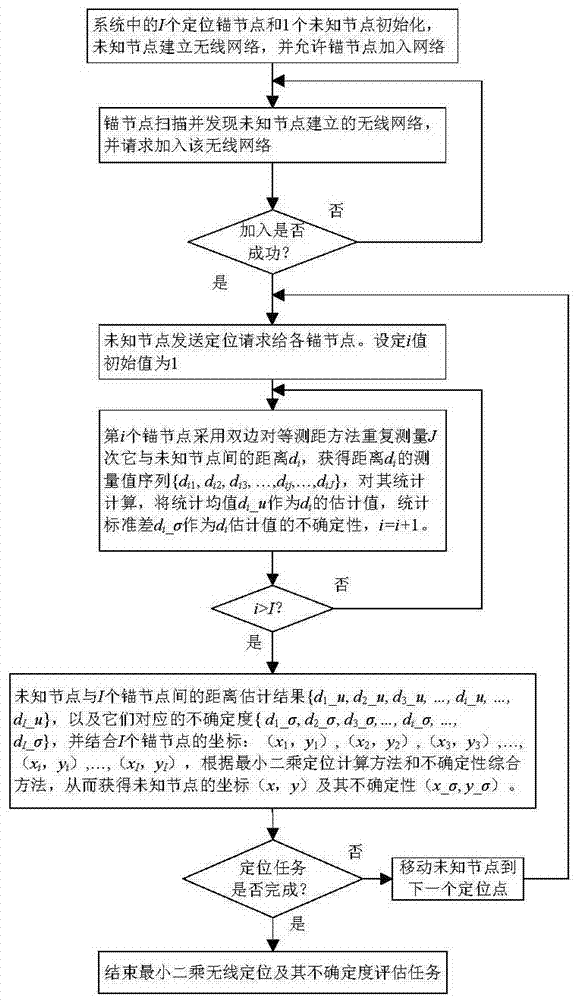
步骤一、系统中有i+1个无线传感器节点，分别为i个定位的锚节点和1个未知节点，它们都具有nanoloc无线射频收发器，并可采用双边对等方法测量得到任意两个节点间的距离估计值，其中i为用户设定的参数，为正整数，且6≤i≤10，本发明中，i取值为9；

步骤二、系统中各个节点进行初始化，未知节点首先建立无线网络，并等待其它节点申请加入网络；

步骤三、i个锚节点初始化成功后，分别采用射频收发器扫描发现未知节点建立的无线网络，并通过射频收发器发送网络加入请求数据包，并成功加入该无线网络，如果加入网络成功，则执行步骤四，否则，执行步骤三；

步骤四、未知节点通过其无线射频收发器广播定位请求数据包，第i个锚节点收到定位请求数据包后，采用双边对等测距方法，通过与未知节点间的4j次数据包交互，获得第i个锚节点与未知节点间的距离di的j次测量值：{di1,di2,di3,…,dij,…,dij}，并进行统计计算，将测量值的统计均值di_u作为距离di估计结果，将测量值的统计标准差di_σ作为距离di估计结果的不确定性，其中i为正整数，且1≤i≤i，i的初始值为1，j为正整数，且1≤j≤j，j为用户设定的正整数，且50≤j≤150，本发明中，j取值为100；

步骤五、i＝i+1，判断i的值是否大于i，若是，则执行步骤六，否则执行步骤四；

步骤六、系统获得了未知节点与i个锚节点间的距离估计结果{d1_u,d2_u,d3_u,…,di_u,…,di_u}，以及它们对应的不确定度{d1_σ,d2_σ,d3_σ,…,di_σ,…,di_σ}，并结合三个锚节点的坐标：{(x1，y1)，(x2，y2)，(x3，y3),…,(xi，yi),…,(xi，yi)},则未知节点的坐标(x，y)按公式(1)进行计算：

其中

步骤七、定位计算结果(x，y)的不确定性(x_σ,y_σ)按公式(2)进行计算：

其中i为正整数，且1≤i≤i，和分别为敏感因子，分别表示定位因素xi、yi和di_u对定位结果的影响程度大小，通过敏感因子值的大小，可识别出对定位影响较大的因素，为改善定位精度提供重要参考信息，xi_σ和yi_σ分别为第i个锚节点横坐标和纵坐标的标准差，由于本发明中，设定锚节点的位置是精确值，因此xi_σ＝0，yi_σ＝0，其中i为正整数，且1≤i≤i，因此，公式(2)可简化为：

步骤八、判断定位计算任务是否完成，如果是，执行步骤九，否则，在下一个定位点上，执行步骤四；

步骤九、结束最小二乘定位及其不确定性分析任务。

附图说明

图1为一种基于最小二乘定位的不确定性分析方法的流程图。

具体实施方式

具体实施方式一：结合图1说明本实施方式，本实施方式所述的一种基于最小二乘定位的不确定性分析方法包括以下步骤：

步骤一、系统中有i+1个无线传感器节点，分别为i个定位的锚节点和1个未知节点，它们都具有nanoloc无线射频收发器，并可采用双边对等方法测量得到任意两个节点间的距离估计值，其中i为用户设定的参数，为正整数，且6≤i≤10，本发明中，i取值为9；

步骤二、系统中各个节点进行初始化，未知节点首先建立无线网络，并等待其它节点申请加入网络；

步骤三、i个锚节点初始化成功后，分别采用射频收发器扫描发现未知节点建立的无线网络，并通过射频收发器发送网络加入请求数据包，并成功加入该无线网络，如果加入网络成功，则执行步骤四，否则，执行步骤三；

步骤四、未知节点通过其无线射频收发器广播定位请求数据包，第i个锚节点收到定位请求数据包后，采用双边对等测距方法，通过与未知节点间的4j次数据包交互，获得第i个锚节点与未知节点间的距离di的j次测量值：{di1,di2,di3,…,dij,…,dij}，并进行统计计算，将测量值的统计均值di_u作为距离di估计结果，将测量值的统计标准差di_σ作为距离di估计结果的不确定性，其中i为正整数，且1≤i≤i，i的初始值为1，j为正整数，且1≤j≤j，j为用户设定的正整数，且50≤j≤150，本发明中，j取值为100；

步骤五、i＝i+1，判断i的值是否大于i，若是，则执行步骤六，否则执行步骤四；

步骤六、系统获得了未知节点与i个锚节点间的距离估计结果{d1_u,d2_u,d3_u,…,di_u,…,di_u}，以及它们对应的不确定度{d1_σ,d2_σ,d3_σ,…,di_σ,…,di_σ}，并结合三个锚节点的坐标：{(x1，y1)，(x2，y2)，(x3，y3),…,(xi，yi),…,(xi，yi)},则未知节点的坐标(x，y)按公式(1)进行计算：

其中

步骤七、定位计算结果(x，y)的不确定性(x_σ,y_σ)按公式(2)进行计算：

其中i为正整数，且1≤i≤i，和分别为敏感因子，分别表示定位因素xi、yi和di_u对定位结果的影响程度大小，通过敏感因子值的大小，可识别出对定位影响较大的因素，为改善定位精度提供重要参考信息，xi_σ和yi_σ分别为第i个锚节点横坐标和纵坐标的标准差，由于本发明中，设定锚节点的位置是精确值，因此xi_σ＝0，yi_σ＝0，其中i为正整数，且1≤i≤i，因此，公式(2)可简化为：

步骤八、判断定位计算任务是否完成，如果是，执行步骤九，否则，在下一个定位点上，执行步骤四；

步骤九、结束最小二乘定位及其不确定性分析任务。

具体实施方案二，本实施方式是对具体实施方式一所述的一种基于最小二乘定位的不确定性分析方法作进一步说明，本实施方式中，采用偏微分的方法，获得最小二乘定位计算过程中各个不确定性因素的敏感因子，评估这些因素的不确定度对定位计算结果的影响程度大小。

具体实施方案三，本实施方式是对具体实施方式一所述的一种基于最小二乘定位的不确定性分析方法作进一步说明，本实施方式中，通过对各个不确定性的综合，获得最小二乘定位计算结果的不确定性，为后续应用处理方法，例如导航决策提供参考。

具体实施方案四，本实施方式是对具体实施方式一所述的一种基于最小二乘定位的不确定性分析方法作进一步说明，本实施方式中，能够有效对最小二乘定位计算中的不确定性进行分析，也可以对改进的最小二乘定位计算过程中的不确定性进行有效分析。

具体实施方案五，本实施方式是对具体实施方式一所述的一种基于最小二乘定位的不确定性分析方法作进一步说明，本实施方式中，能够有效对定位计算中的不确定性进行分析，也可以对三维及多维定位计算过程中的不确定性进行分析。