多径环境下GNSS接收机信号参数估计方法与流程

本发明涉及一种能够被应用于车辆、飞行器等设备在各种复杂环境下的高精度导航定位领域，也能用于大地和海洋测绘、姿态确定、交通安全、物理勘探等技术领域的多径环境下gnss接收机信号参数估计方法。

背景技术：

gnss(globalnavigationsatellitesystem，全球导航卫星系统)以人造地球卫星作为导航台的星基无线电导航系统，为全球陆、海、空、天的各类军民载体提供全天候、高精度的位置、速度和时间信息。在利用gnss进行导航定位时，gnss信号从卫星端传播到接收机端时，会存在各种测量误差，包括卫星钟差、接收机钟差、电离层误差、对流层误差、多径效应影响和噪声等，直接影响定位精度。在以上的误差项中，除了多径效应以外，其它的误差项都可以通过差分技术进行消除。当gnss接收机处于多径环境下时，gnss接收机天线除了接收到一路从gnss卫星经直线传播的电磁波信号之外，还会接收到一个或多个由该电磁波经周围环境反射后的信号，使gnss接收机对信号的测量产生误差和对信号的跟踪造成困难，这个就称为多径效应，由此引起的测量误差成为多径误差。在gnss的高精度应用中，多径是最难以处理的误差源，会对导航与定位结果造成严重危害。

目前已有的方法大致可以分为:基于相关器技术的方法、基于导航解算的方法与基于多径参数估计的方法。基于相关器技术的方法中研究较多的有窄相关技术、双相关器技术、包括hrc(highreso-lution技术、ashtcch公司的strobecorrelator技术、novatel公司的pa)技术，early-i，atc斜率技术，eerlylearly2跟踪器等及vision丰h关器技术等。多径信号参数估计方法的主要实现形式有ml方法、卡尔曼线性滤波、非线性滤波、rake接收机93等。这些估计方法虽然具有较高的估计精度和适应性，但是需要更多相关器，实现复杂，实时性较差。这些技术对于长延迟多径信号均有较好的制效果，但是对于短延迟(小于0.1码片)的多径信号没有起到改善作用。而短延迟的多径信号对载波相位测量的影响较为严重。这一点是信号处理多径抑制技术的局限性。基于导航解算的方法包括加权、码伪距平滑、多频率测量、多径衰落信道模型、传感器融合处理等。这些方法由于是在观测量的后端处理过程使用，不需要增加相关器的个数。但是只能起到对误差的补偿作用，对于多径效应的消除效果同样有限，以作为辅助的多径效应消除手段而使用。

gnss接收机只有采取一定的抗多径措施才能满足精度定位的要求。对于多径效应的抑制主要从天线设计、改善接收机技术以及提升数据信息处理精度多方面考虑。当前多径抑制技术,来自地面的多径效应可以通过天线设计加以抑制，但对来自天线上方的多径信号难以通过天线设计进行有效的抑制，它需要通过接收机的改进或者信号处理技术来实现，而且也很难应用在低成本和小体积的接收机中。改进接收机技术从硬件方面考虑，侧重于硬件实现的低复杂度，对于多径误差有一定的抑制效果，但对于短时延多径信号的抑制作用甚微。这些方法可以消除来自天线平面以下的多径信号，但是对于来自接收机上方的多径信号则无能为力。另外，对多径信号进行建模处理，将多径误差的抑制问题转化为直达信号的时延估计问题，从而达到抑制多径误差的目的，是一种好的解决思路，这个就是多径误差抑制的信号参数估计方法。多径会导致鉴相函数的过零点偏移，从而产生码测量误差，而且在复杂环境中，存在的更多的是短多径(多径信号相对于直达信号时延小于0.5码片)，在短多径信号存在时，即使采用现有的最佳方法，6m的峰值距离误差也是很常见的，这是因为当直达路径与多径路径时延相关间隔很小时，从接收信号中估计直达路径延迟是一个非常复杂的参数估计问题。理论上，如果接收机受到个多径信号的影响就需要进行多次迭代计算，但在实际环境中，事实上并不知道存在多少个多径信号，而且肘也不是一个常数。在迭代计算的过程中将多径信号考虑在内，利用并行通道的窄相关采样估计出直接信号和多径信号的幅度、延迟和相位，分析延迟最小的信号，认为是直接信号，其它较大延迟的信号认为是多径信号分量被消除，并行处理通道与多径误差包络曲线由于需要处理的信息较多，技术的实时性较差，这就决定了只能应用于多径变化较为缓慢的场合。针对多相关器多径估计问题，现有技术提出了基于最大似然估计的多径参数估计方法来减小短多径误差。最大似然法采用的参数化多径抑制方法，考虑多径信号的干扰，将接收信号进行具有不同幅度、相位和时延的参数化建模，再通过最大似然原理求似然函数的极大值，从而得到直射信号时延和多径信号时延的联合估计，目前应用最成功的是medll跟踪环路的设计，并已在接收机端有实际应用。多径衰减技术(mmt)对于二径情况，通过对对数似然函数中多径参数的非线性变换，将对数似然函数的求解过程降低到二维空间进行搜索，而不是原先的6维，降低了多径参数估计的复杂度，具有较好的多径抑制性能，但是该技术只适用于两路路径的情况，在其它情况下该技术的多径抑制性能下降。m.sahmoudi提出的快速迭代最大似然算法(fimla，fastiterativemaximum-likelihoodalgorithm)，它主要利用gnss信号模块的结构和扩频码的周期性，并认为时延和幅度在观测时间内恒定不变，利用最大似然法对信号进行跟踪，并通过newton算法求得各信号参数的最优值，但因为其采用了迭代方法，不能保证每次迭代都收敛到全局最优点。在实际应用中,由于多路径误差的随机性非常强,靠建立误差模型修正多路径误差无法实现。数据建模或差分处理等常用的误差处理技术无法消除多径效应造成的误差。目前还没有一种技术能够非常好地解决接收机面临的多径误差问题。

技术实现要素：

本发明的目的是针对多径环境对gnss接收机测量的影响，提供一种计算量相对较小、估计精度高、适应性强的信号参数估计方法。

本发明解决现有技术问题所采用的技术方案是：一种多径环境下gnss接收机信号参数估计方法，其特征在于包括如下步骤：在构造的多相关器结构的gnss接收机模型中，根据相关器的数目确定各相关器之间的相关间隔；射频通道输出的中频信号进入gnss接收机多相关器结构的跟踪环路中，与同相支路和正交支路的载波信号进行混频，解调出基带信号，将得到的基带信号与接收机复现的本地信号进行相关运算，得到各个相关器的采样输出值；再根据各个相关器的采样输出值建立gnss接收机输出表达式：ui＝hy+ni和uq＝hz+nq；然后，通过最大似然估计单元，根据多个相关器得到相关函数的多个采样值，利用最大似然法构造似然函数，再进行网格化搜索估计，根据最大似然估计法准则和网格化搜索得到gnss接收机信号的幅度、码片延迟和载波相位值的估计值；最后，采用分段线性插值法进一步估计出直达信号的码片延迟和载波相位值，其中，ui为gnss接收机i支路中各相关器的采样输出值组成的向量,uq为gnss接收机q支路中各相关器的采样输出值组成的向量,h各个相关值组成的(2m+1)×m的矩阵；y和z分别为包含有接收信号幅度和相位值的位置参数向量；ni和nq为加性高斯噪声向量。

本发明相比于现有技术具有如下有益效果：

计算量相对较小。本发明采用构建的多相关器结构的gnss接收机模型，各相关器的延迟是确定可知的，利用最大似然法构造似然函数，再进行网格化搜索估计时，更容易确定接收信号的幅度、码片延迟和载波相位值，且计算量会相对较小。

估计精度高。本发明针对多径环境对gnss接收机测量的影响，gps信号传播环境的复杂性，使用最大似然估计法准则和网格化搜索进行载波相位和频率的估计,利用最大似然法估计得到信号各参数之后，再采用分段线性插值法进一步估计直达信号码片延迟，准确估计出直达信号的码片延迟和载波相位值，提高了直达信号码片延迟值估计的精度。利用分段线性插值法技术由载波相位估值来确定直达信号码延迟，降低多普勒频移对伪码延迟环的直接影响,从而得到准确的伪码延迟估计,提高了伪码延迟环的动态性能。

适应性强。本发明设计了多相关器结构的gnss接收机跟踪环路，由于其相关器的数目可以调整而满足估计精度要求，因此在复杂环境下多径信号数目未知的情况下也能使用，并可达到较高的估计精度。

附图说明

下面结合附图和实施例对本发明进一步说明。

图1为本发明多径环境下gnss接收机信号估计方法的原理流程框图。

图2为本发明多相关器结构的gnss接收机结构模型。

图3为本发明接收信号与各相关器延迟的关系。

具体实施方式

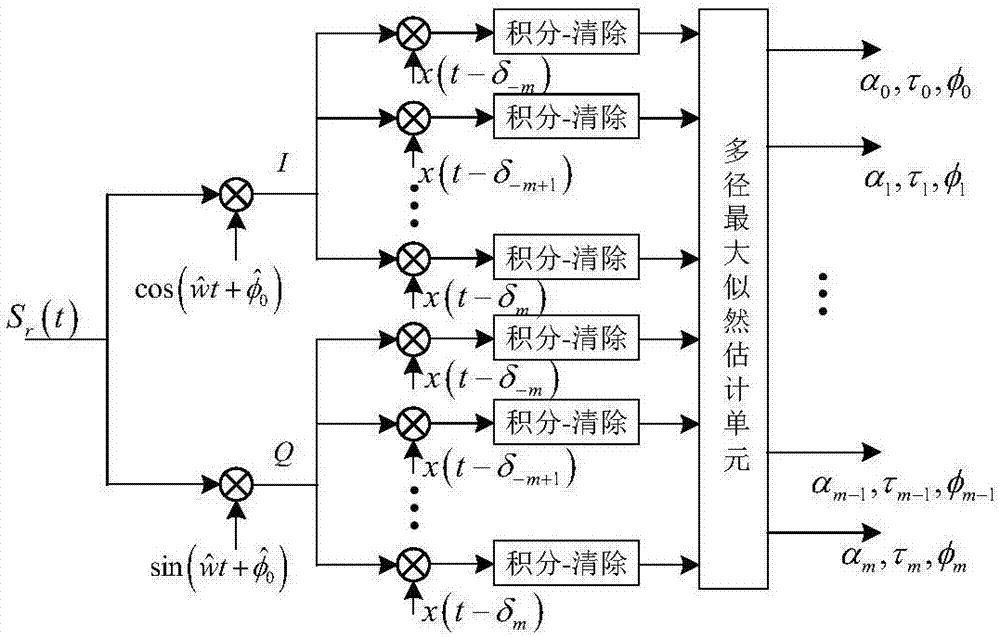
参照图1。根据本发明，多径环境下gnss接收机信号参数估计方法的工作原理是：首先，在gnss接收机中，构建多相关器结构的gnss接收机跟踪环路，将同相支路的i支路和正交支路的q支路分别设为总数为2m的相关器。在构造的多相关器结构的gnss接收机模型中，根据相关器的数目确定各相关器之间的相关间隔；射频通道输出的中频信号与gnss接收机多相关器结构的跟踪环路中同相支路和正交支路的载波信号进行混频，解调出基带信号，然后，将得到的基带信号与接收机本地复现的信号进行相关运算，得到采样输出值；再根据各个相关器的采样输出值建立gnss接收机输出表达式：同相支路和正交支路，通过最大似然估计单元，采用多个相关器得到相关函数的多个采样值，利用最大似然法构造似然函数，再进行网格化搜索估计，根据最大似然估计法准则和网格化搜索得到gnss接收机信号的幅度、码片延迟和载波相位值的估计值；最后，采用分段线性插值法进一步估计出直达信号的码片延迟和载波相位值。

参照图2。在设计的多相关器结构gnss接收机的跟踪环路中，i支路和q支路分别设计总数为2m的相关器，射频通道输出的中频信号sr(t)分别与i支路的载波信号和q支路的载波信号进行混频，将得到的基带信号输入各个相关器中进行相关运算，进行采样得到相关函数的采样值，最后再输入最大似然估计单元对输出值进行信号参数估计，得到相应的幅度、码片延迟和载波相位估计值。上述相关器为图2所示的积分-清除器，其中，为本地载波信号的角频率，为相位初始估计值。

在图2、图3中，根据相关器的数目确定各相关器之间的相关间隔延迟。

各相关器之间的关系为δm-δ-m＝2mδ，选择mδ＝tc，其中，δm和δ-m分别为超前和滞后最远的相关间隔延迟，2m为同相或正交支路上的相关器的总数，tc为一个码片的周期，因此相对应的相邻相关器之间的相关间隔为δ＝tc/m。

(2)图2，中频信号与gnss接收机中同相支路和正交支路的载波信号进行混频，解调之后得到基带信号。

gnss接收机同时接收到m条多径信号时，下变频之后的中频信号如式(1)所示，忽略导航电文数据和载波相位幅度之后，得中频信号：得中频信号sr(t)：

式中，t为任一时刻；i＝0为直达信号,m表示多径信号数量；α0＝1，αi(i≠0)为第i条多径信号的幅度衰减系数；x(t)为调制有伪码、载波、导航电文的复合信号；τi为第i个码片延迟；w为卫星信号的中频角频率；φi为多径信号相对直达信号的相位延迟；n(t)为噪声信号。

进入gnss接收机的中频信号sr(t)分别与图2中所示的同相支路的载波信号以及正交载波信号进行相乘混频，这样经解调之后得到i支路和q支路的基带信号和基带信号

(3)基带信号与接收机本地复现的信号进行相关运算，得到采样输出值。

进入gnss接收机的中频信号分别与图2中所示的同相支路的载波信号以及正交载波信号进行相乘混频，这样经解调之后得到i支路和q支路的基带信号和基带信号。

基带信号与接收机本地复现的信号进行相关运算，得到采样输出值。

多相关器gnss接收机中，步骤(2)得到的基带信号分别于本地复现的一组信号进行相关运算，假设相关积分时间为，可以得到：为t，可以得到：

式中，ui(δk)和ui(δk)分别为同相支路和正交支路中各相关器输出的采样值，k表示第k个相关器，k＝-m,-m+1,…,m-1,m；δk＝kδ为相关器相关间隔延迟，其中δ＝δk+1-δk＞0为相邻两个相关器之间的相关间隔，而且δ0＝0，t为相关积分时间，和别为i支路和q支路的基带信号；x(t-δk)为本地复现的信号；t为采样时间。

那么基带信号与本地复现信号相乘并积分之后，由式(2)和(3)得到第个相关器的采样输出值可以表示为：

式中，ui(δk)和ui(δk)分别为同相支路和正交支路中各相关器输出的采样值；i＝0为直达信号,m表示多径信号数量；α0＝1，αi(i≠0)为第i条多径信号的幅度衰减系数；为相位初始估计值；φi为多径信号相对直达信号的相位延迟；为基带信号与本地复现信号x(t-δk)之间的相关函数；δk＝kδ为相关器相关间隔延迟；τi为第i个码片延迟；ni(δk)和nq(δk)均为零均值的高斯白噪声。

(4)根据各个相关器的采样输出值建立gnss接收机输出表达式，利用最大似然估计法和网格化搜索得到gnss接收机信号的幅度、码片延迟和载波相位值的估计值。

结合式(4)、式(5)和图2中gnss接收机多相关器结构，建立gnss接收机输出表达式：

ui＝hy+ni(6)

uq＝hz+nq(7)

式中，ui为i支路中各相关器的采样输出值组成的向量，ui＝[ui(δ-m),…,ui(δm)]^t，δm和δ-m分别为超前和滞后最远的相关间隔延迟；；uq为q支路中各相关器的采样输出值组成的向量，uq＝[uq(δ-m),…,uq(δm)]^t，δm和δ-m分别为超前和滞后最远的相关间隔延迟；h为式(4)和(5)中各个相关值组成的(2m+1)×m的矩阵；y和z分别为包含有接收信号幅度和相位值的位置参数向量；ni和nq为加性高斯噪声向量。

考虑支路，根据加性高斯噪声向量的概率密度分布特点，利用最大似然估计方法得到式(6)的最大似然函数为：

式中，σi为ni的协方差矩阵；t为转置运算。

根据图2所示的gnss接收机结构图，确定相关器个数的值，选择码片延迟估计τi＝δk，τi+1＝δl，其中δk＜δl，进而确定τ之后，便可以得到最大似然估计值y：

y＝(h^tσ^-1h)^-1h^tσ^-1ui(9)

根据多相关器的网格化搜索，首先确定多相关器s组不同组合的网格化延迟，每次搜索确定系数矩阵h并保存相应的矩阵，再根据式(9)计算不同的码片延迟组合时对应的输出值再计算每个码片延迟组合的残差，并在s组残差中搜索最小值得到码片延迟估计值和输出估计值再根据确定的计算q支路中码片延迟组合对应的再利用最大似然法和网格化搜索确定的和对第i路信号，按照式(10)和式(11)求得信号幅度的估计值和载波相位估计值

式中，为信号幅度的估值，为i支路输出估计值向量的第i个值，为q支路输出估计值向量的第i个值，φi为载波相位估值。

(5)采用分段线性插值法准确估计出直达信号的码片延迟和载波相位值。

根据式(4)得到的相关器采样输出式(10)、(11)得到的信号参数估计，可知信号的相关函数可为：

式中，为直达信号码片延迟的估值，δj为第j个相关器相关间隔延迟，为直达信号幅度的估值，为多径信号幅度的估值，为直达信号载波相位的估值。

选取三个点其中，p-1、p0、p1分别表示三个相邻点，δ-1，δ0，δ1分别为三个相邻点的相关器间隔，然后采用分段线性插值法得到更为精确的主峰位置码片延迟估计值。分段线性插值法通过构造两条曲线，其中一条曲线经过p0点和中较小的点，另外一条直线的斜率与第一条直线的斜率相反，且经过中较大的一点，此时两条直线的交点所对应的码片延迟即为分段线性插值法估计得到的直达信号码片延迟值。