一种确定氧化锌避雷器最大允许阻性泄漏电流的方法与流程

本发明属于高压电器技术领域，具体涉及一种确定氧化锌避雷器最大允许阻性泄漏电流的方法。

背景技术：

避雷器在电力系统中主要用于限制由线路传来的雷电过电压或操作引起的内部过电压，保证系统的正常运行。氧化锌避雷器由于具有优良的非线性特性，保护特性好、通流容量大、结构简单，提供更好的保护水平和更大的保护裕度，得到了广泛的运用。尽管氧化锌避雷器材料生产水平不断提高，但由于长期承受工频电压、过电压及受潮等因素影响，阀片会逐渐老化，泄漏电流增加并导致温度升高，最终引发电网事故。

引发氧化锌避雷器出现故障的因素主要有受潮、短路等，受潮事故占氧化锌避雷器总事故率的60％以上。氧化锌避雷器运行状态的变化直接反映在其阻性泄漏电流的变化上，阻性泄漏电流的增大和突变是导致避雷器故障的主要原因，因此，阻性泄漏电流的监测是检验氧化锌避雷器故障的有效手段。

根据辽宁省防雷技术服务中心的相关规定，将泄漏电流的数值变动超过10％的压敏电阻判定为失效的压敏电阻。通过氧化锌避雷器阻性泄漏电流变动率来反应其受潮程度，考虑氧化锌避雷器的稳定运行及电力系统的安全裕量，得到阻性泄漏电流变化情况与氧化锌避雷器受潮状态的关系，得到氧化锌避雷器的最大允许阻性电流。

技术实现要素：

针对现有技术的不足，本发明提出一种确定氧化锌避雷器最大允许阻性泄漏电流的方法，以达到方便、直观地得到氧化锌避雷器中各个氧化锌电阻片的受潮程度，较好地对氧化锌避雷器的故障进行预警的目的。

本发明的技术方案如下：

一种确定氧化锌避雷器最大允许阻性泄漏电流的方法，包括以下步骤：

步骤1、建立氧化锌避雷器的三维实体模型；

步骤2、对建立的氧化锌避雷器的三维实体模型的非金属部件进行划分网格；

步骤3、设定网格属性和氧化锌避雷器三维实体模型的边界条件，加载氧化锌避雷器实际的工作电压；

步骤4、对氧化锌避雷器在实际的工作电压下实际运行情况的电位进行计算，获取氧化锌避雷器各氧化锌电阻片的电位值，根据氧化锌电阻片两端的电位差和氧化锌电阻片的电容值获得氧化锌电阻片的容性泄漏电流值；

步骤5、根据氧化锌电阻片的结构、尺寸以及氧化锌电阻片上下两个面的电位降，计算不同电阻率下流过氧化锌电阻片的阻性泄漏电流；

步骤6、根据氧化锌电阻片的容性泄漏电流值与阻性泄漏电流值，计算氧化锌避雷器的阻性泄漏电流变动率，得到阻性泄漏电流变化情况与氧化锌电阻片电阻率的关系；

步骤7、氧化锌电阻片的阻性泄漏电流变动率超过阈值时的压敏电阻判定为失效的压敏电阻，计算氧化锌避雷器阻性泄漏电流变动率达到阈值时的阻性泄漏电流，即为最大允许阻性泄漏电流；

步骤8、根据实时监测到的氧化锌避雷器的阻性泄漏电流值大小，判断氧化锌避雷器的受潮程度，阻性泄漏电流值越大，氧化锌避雷器受潮越严重。

所述步骤3，包括：

步骤3-1、设定网格属性为氧化锌避雷器各元件的相对介电常数；

步骤3-2、对氧化锌避雷器电位的计算通过电位控制方程来进行；

步骤3-3、设定氧化锌避雷器三维实体模型的边界条件；

步骤3-4、加载氧化锌避雷器实际的工作电压。

采用自由划分网格的方法对建立的氧化锌避雷器的三维实体模型的非金属部件进行划分网格，对氧化锌避雷器三维实体模型的各个元件按照从内到外的顺序依次进行网格划分，同一类型的元件一起划分。

所述步骤4中，氧化锌电阻片的容性泄漏电流值的计算公式如下：

ii＝ui×ci×2πf(1)

其中，ii表示流过第i片氧化锌电阻片的容性泄漏电流值，ui表示第i片氧化锌电阻片两端的电位差；ci表示第i片氧化锌电阻片的电容值；f表示工频。

所述步骤6中，氧化锌电阻片的阻性泄漏电流变动率的计算公式如下：

有益效果：

本发明提出一种确定氧化锌避雷器最大允许阻性泄漏电流的方法，该方法使人们较为直观、方便地得到氧化锌避雷器中各个氧化锌电阻片的受潮情况，并通过对氧化锌避雷器阻性泄漏电流变动率的计算来判断氧化锌避雷器的受潮程度，可以较好的对氧化锌避雷器的故障情况进行评估，从而对氧化锌避雷器进行有效的预警；该方法具有简单直观、计算精确度高、数据分析清晰等明显特点。

附图说明

图1为本发明一种实施例的氧化锌避雷器最大允许阻性泄漏电流的确定方法流程图；

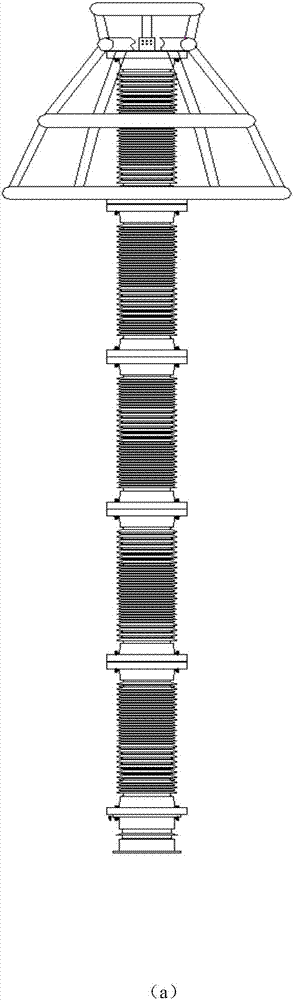
图2为本发明一种实施例的1000kv电力系统用氧化锌避雷器总装图和元件装配图，其中，(a)为总装图；(b)为元件装配图；

图3为本发明一种实施例的1000kv电力系统用氧化锌避雷器总体建模和内部建模图，其中，(a)为总体建模图；(b)为内部建模图；

图4为本发明一种实施例的氧化锌避雷器各元件网格划分图，其中，(a)为氧化锌电阻片示意图，(b)为电容器示意图；(c)为瓷外套；

图5为本发明一种实施例的不同受潮程度下氧化锌避雷器阻性泄漏电流变动率曲线图。

具体实施方式

下面结合附图对本发明一种实施例做详细说明。

本发明实施例中的确定氧化锌避雷器最大允许阻性泄漏电流的方法，流程如图1所示，包括以下步骤：

步骤1、根据氧化锌避雷器的各元件尺寸及实际构造，采用ansys有限元软件建立氧化锌避雷器的三维实体模型；

本发明实施例中，如图2(a)～(b)所示，是1000kv电力系统用氧化锌避雷器总装图和元件装配图；其中，氧化锌电阻片为环状，外径为136mm，内径为54mm，厚度为20mm；瓷套外壳厚度为14mm；法兰为环状，外径为1010mm，内径为960mm，厚度为110mm；均压环为双层结构，上层均压环环径为200mm，安装在距氧化锌避雷器顶端1180mm处，下层均压环环径为200mm，安装在距氧化锌避雷器顶端2300mm处；本发明实施例中，对氧化锌避雷器的实物进行合理取舍，忽略金属螺母、均压环的连接支管和瓷外套伞群，严格按照氧化锌避雷器的实物尺寸进行三维实体模型的建立，如图3(a)～(b)所示，是1000kv电力系统用氧化锌避雷器的总体建模和内部建模图。

步骤2、对建立的氧化锌避雷器的三维实体模型的非金属部件进行划分网格；

本发明实施例中，采用自由划分网格的方法对建立的氧化锌避雷器的三维实体模型的非金属部件进行划分网格，选择类型为solid123的四面体网格，对氧化锌避雷器三维实体模型的各个元件按照从内到外的顺序依次进行网格划分，同一类型的元件一起划分，具体划分的顺序和网格大小为：

氧化锌电阻片，四面体网格边长为20mm；电容器，四面体网格边长为18mm；瓷外套，四面体网格边长为15mm；壳内空气域，四面体网格边长为45mm；壳外空气域，四面体网格边长为800mm；金属元件内部不存在电场，故不进行网格划分，如图4(a)～(c)所示，是氧化锌避雷器各元件的网格划分图，图中网格的节点属性为电位值；

步骤3、在ansys有限元软件中设定网格属性和氧化锌避雷器三维实体模型的边界条件，加载氧化锌避雷器实际的工作电压；

步骤3-1、设定网格属性为氧化锌避雷器各元件的相对介电常数；

本发明实施例中，氧化锌避雷器正常工作状态下电位分布数值计算按照静电场来求解，具体说明如下：

氧化锌避雷器平时工作在工频的持续运行电压下，氧化锌避雷器的电场为工频系统的电准静态场；在电力系统中，输电线路周围工频电场的频率一般为50hz，波长约为6000km，变电站之间的输电线路长度一般只有200km左右；根据准静态场的定义：电磁波以速度v传播通过所研究的电磁系统的最大线度尺寸l的时间远远小于该电磁波的周期t时，电场和磁场之间耦合作用极弱，可以将该电磁场视为准静态电磁场。在对避雷器电位分布的计算中，涉及物体的最大尺寸不超过100m，满足上述定义，因此，输电线路产生的工频电场可以近似看作为电准静态场，即其中b表示磁感应强度，t表示时间。

因此，麦克斯韦方程组表示为：

其中，为矢量微分算符，h为磁场强度；b为磁感应强度；d为电位移；e为电场强度；j为电流密度；ρ为电荷密度；

对求散度，则有：

根据电场是无旋的，仍可以用标量电位φ来描述电场强度e：

此时电场和磁场已经是非耦合的；对电场，同时考虑了材料的电导σ和介电常数ε的电准静态场的控制方程可表示为：

对于时谐场，标量电位φ用向量表示，式(4)变为：

对于场域中的导体，例如输电线、杆塔、法兰、大地等，其电导σ数量级一般在以10⁶上，相对介电常数则一般不会超过10，传导电流与位移电流之比为：

其中，jc表示传导电流，jd表示位移电流，ω表示频率。

可以看出，在工频系统中传导电流远远大于位移电流，因此，忽略(5)中第二项，则其控制方程可以表示为：

可以看出，导体中电位不相等，但在工频下差别很小，通常认为导体中的电位相同，在计算中悬浮导体可按静电场中的处理方法进行；因此，式(7)无须求解。

对于场域中的介质，如空气，其电导率近似认为0，而瓷套、电阻片、绝缘杆等，其电导σ数量级小于10¹²，相对介电常数则一般不会超过1000，传导电流与位移电流之比为：

此时位移电流远大于传导电流，则有：

电准静态场中，ω和ε可以看作常数处理，则式(9)就可以化简成：

由此可见，准静态电场的计算遵循着和静电场完全相似的规律；因此，氧化锌避雷器正常运行情况下的电位分布的数值计算完全可以按照静电场来进行求解；考虑位移电流，将相对介电常数设定为计算模型的网格的属性，查阅资料，各个元件的相对介电常数具体如下：

氧化锌电阻片的相对介电常数设定为650，电容器的相对介电常数设定为5，金属材料的相对介电常数极大，这里设定为3000，瓷外套的相对介电常数设定为7.6，空气的相对介电常数设定为1。

步骤3-2、在ansys有限元软件中对氧化锌避雷器电位的计算通过电位控制方程来进行；

公式如下：

步骤3-3、在ansys有限元软件中设定氧化锌避雷器三维实体模型的边界条件；

本发明实施例中，氧化锌避雷器电场分布的研究是一个有限区域的问题，考虑第一类边界条件和第二类边界条件；

第一类边界条件又称强加边界条件，具体如下：

φ|γ1＝g(p)(12)

其中，g(p)为位置的一般函数，特殊情况下可以为零或是常数，它表明电势在某个点的值是给定的，本发明实施例中，空气域外边界、顶端法兰外表面和均压环外表面采用第一类边界条件。

第二类边界条件又称自然边界条件，具体如下：

其中，h(p)为一般函数，n为边界的外向法向矢量，特殊情况下可以为零或是常数，本发明实施例中，不同介质材料部件的接触表面采用第二类边界条件。

本发明实施例中，对于氧化锌避雷器的每一个电位悬浮导体来说，采用耦合电位自由度的方法来处理，即认为其表面上每一个节点的电位均相等，且等于同一个待求值；

本发明实施例中，氧化锌避雷器工作在户外，周围空气域边界无限大，在进行电场分布计算时，将无界域问题截断为有界域问题，即设定计算边界为氧化锌避雷器三维实体模型实际尺寸的5倍，便可满足计算精度的要求。

本发明实施例中，两种电介质交界面处设置电介质的电容率。

本发明实施例中，基于设定的边界条件，对于氧化锌避雷器的三维电场的求解问题，用φ＝φ(x，y，z)来描述其场的分布，则变为在整个求解域内满足边界条件的等价变分泛函问题：

其中，x、y、z为三维坐标向量，为各个剖分单元的能量泛函总和；

步骤3-4、加载氧化锌避雷器实际的工作电压；

本发明实施例中，对氧化锌避雷器最顶端法兰以及均压环处施加638kv的持续运行电压，对氧化锌避雷器底座及空气域边界处施加零电位，即接地处和视为无穷远处；

步骤4、对氧化锌避雷器实际运行情况的电位进行计算，获取氧化锌避雷器各氧化锌电阻片的电位值，根据氧化锌电阻片两端的电位差和氧化锌电阻片的电容值获得氧化锌电阻片的容性泄漏电流值；

本发明实施例中，使用ansys有限元软件对1000kv电力系统用氧化锌避雷器的电场模型进行计算，得到氧化锌避雷器上各处氧化锌电阻片的电位值，根据氧化锌避雷器容性泄漏电流理论计算公式，计算出流过各个氧化锌电阻片的容性泄漏电流值；

公式如下：

ii＝ui×ci×2πf(1)

其中，ii表示流过第i片氧化锌电阻片的容性泄漏电流值，ui表示第i片氧化锌电阻片两端的电位差；ci表示第i片氧化锌电阻片的电容值；f表示工频50hz；

步骤5、根据氧化锌电阻片的结构、尺寸以及计算得到的氧化锌电阻片上下两个面的电位降，计算不同受潮程度(即不同电阻率)下流过氧化锌电阻片的阻性泄漏电流；

氧化锌电阻片的电阻率能够反应其受潮程度，电阻率越大，受潮越严重，赋予氧化锌避雷器三维实体模型中氧化锌电阻片不同的电阻率，本发明实施例中，氧化锌电阻片为环状，外径为136mm，内径为54mm，厚度为20mm；根据氧化锌电阻片的结构、尺寸以及电阻率，利用电阻计算公式其中r、ρ、l、s分别为氧化锌电阻片的电阻值、电阻率、厚度及横截面面积，计算出氧化锌电阻片的电阻值大小，并根据氧化锌避雷器上各处氧化锌电阻片的电位值，计算出不同受潮程度下流过氧化锌电阻片的阻性泄漏电流。

步骤6、根据氧化锌电阻片的容性泄漏电流值与阻性泄漏电流值，计算氧化锌避雷器的阻性泄漏电流变动率，得到阻性泄漏电流变化情况与氧化锌避雷器受潮状态(氧化锌电阻片电阻率)的关系；

氧化锌避雷器的阻性泄漏电流变动率计算公式如下：

本发明实施例中，分别计算了1000kv电力系统用氧化锌避雷器不同受潮程度下(氧化锌电阻片电阻率分别为80mω.m、50mω.m、30mω·m和20mω·m)氧化锌电阻片的阻性泄漏电流变动率，如图5所示。

步骤7、氧化锌电阻片的阻性泄漏电流变动率超过阈值时的压敏电阻判定为失效的压敏电阻，计算氧化锌避雷器阻性泄漏电流变动率达到10％时的阻性泄漏电流，即为最大允许阻性泄漏电流；

根据辽宁省防雷技术服务中心的相关规定，将泄漏电流的数值变动超过10％的压敏电阻判定为失效的压敏电阻，氧化锌电阻片是优良的压敏电阻材料。

本发明实施例中，计算得到1000kv电力系统用氧化锌避雷器的最大允许阻性泄漏电流为0.31ma。

步骤8、利用阻性泄漏电流变化情况与氧化锌避雷器受潮状态的关系，根据实时监测到的氧化锌避雷器的阻性泄漏电流值大小，判断氧化锌避雷器的受潮程度，阻性泄漏电流值越大，氧化锌避雷器受潮越严重，根据计算得到的阻性泄漏电流变动率与氧化锌电阻片失效临界值(即氧化锌电阻片最大允许阻性泄漏电流)对比，可以对氧化锌避雷器因受潮导致的故障进行预警。