广义帕累托分布参数显式双分位点估计方法与流程

本发明属于雷达目标检测技术领域，具体涉及一种双分位点估计方法，可用于在海杂波背景下确定海杂波幅度分布模型的形状和尺度参数。

背景技术：

海杂波背景下的目标检测是雷达的一个重要应用领域。

复合高斯模型是目前学者广泛认可的海杂波模型，它是慢变的正随机变量纹理分量和快变的复高斯随机向量散斑分量的乘积。当海杂波的纹理分量服从逆伽马分布时，海杂波幅度服从广义帕累托分布。广义帕累托分布模型下最优检测器的结构已经获得。最优检测器的结构依赖于海杂波模型的形状参数和尺度参数，如何从复杂海杂波场景中有效精确估计出海杂波模型的参数成为海面目标检测的关键。

常用的参数估计方法有矩估计，分数阶矩估计和最大似然估计方法。但是当形状参数的真实值处于特定范围时，矩估计与分数阶矩估计方法不能正确的估计出形状参数。最大似然估计方法对形状参数的真实值所处的范围没有要求，它比矩估计具有更高的精度，但该方法计算量大而且依赖于初始值的选取。这三种方法都是基于基本假定：所使用的样本是纯杂波数据。然而，实际获得的海杂波样本中常包含少量具有很大幅度的岛礁回波、目标回波构成的异常散射单元。此类异常样本会导致这三种方法的估计精度急剧下降。文献“p-l.shuiandm.liu,"subbandadaptiveglrt-ltdforweakmovingtargetsinseaclutter,"ieeetrans.aerosp.electron.syst.,52(1):423-437,2016.”提出双分位点估计方法，该方法对异常样本具有稳健性，但该文献只明确给出了样本累计概率取0.5和0.75时的参数估计方法，当样本累计概率取其他值时，没有得到形状参数和尺度参数的显式解，而且样本累计概率取0.5和0.75时的参数估计方法估计结果的准确性不够。

技术实现要素：

本发明的目的在于针对上述现有技术的不足，提出一种广义帕累托分布参数的显式双分位点估计方法，以实现对广义帕累托分布的形状参数和尺度参数的精确和稳健估计。

为实现上述技术目的，本发明的技术方案包括如下：

(1)利用雷达发射机发射连续的脉冲信号，雷达接收机接收回波数据，在回波数据中，选取n个杂波数据，对n个杂波数据进行取模并按升序排列，得到杂波幅度递增序列z1,z2,...,zt,...,zn，其中，zt表示杂波幅度递增序列中第t个杂波幅度，t＝1,2,...,n；

(2)确定广义帕累托分布的概率密度函数f(r)：

其中，r表示杂波的幅度，为概率密度函数的自变量，λ表示广义帕累托分布的形状参数，η表示广义帕累托分布的尺度参数；

(3)根据广义帕累托分布的概率密度函数f(r)，得到累积分布函数f(r)：

(4)给定大于1的正数q，选取两个不同的样本累计概率α和β，并使得样本累计概率α和β满足：

(5)根据正数q的取值，得到分位点与广义帕累托分布形状参数λ和尺度参数η的关系式；

(5a)根据正数q的取值，计算中间变量u：

当q＝2，

当q＝3，

当q＝4，其中，ψ表示中间变量，

当q＝5，对求唯一正根得到u；

当q＞5或q为小数时，利用迭代法，选取迭代初始值u0∈(1,+∞)，令得到中间变量

其中，rα表示样本累计概率为α时的分位点，rβ表示样本累计概率为β时的分位点，u0表示中间变量u的迭代初始值，ui表示中间变量u的第i次迭代值，ui+1表示中间变量u的第i+1次迭代值；

(5b)利用中间变量u，得到分位点与广义帕累托分布形状参数λ和尺度参数η的关系式：

(6)利用杂波幅度递增序列z1,z2,...,zt,...,zn，计算每个分位点的估计值：

其中，sα表示分位点rα的估计值，sβ表示分位点rβ的估计值，表示杂波幅度递增序列中第n1个杂波幅度，表示杂波幅度递增序列中第n2个杂波幅度，round(nα)表示最接近nα的整数，round(nβ)表示最接近nβ的整数；

(7)利用(6)计算出的两个分位点的估计值sα和sβ分别代替步骤(5)中的分位点rα和rβ，得出广义帕累托分布的形状参数估计值和尺度参数估计值

本发明与现有技术相比具有以下优点：

1)由于本发明使用分位点估计，相比已有的矩估计和分数阶矩估计方法，对形状参数的真实值所处的范围没有要求，具有更高的准确性。

2)由于本发明使用分位点估计，只考虑分位点以左的样本，可以有效避免分位点右侧功率较大的异常样本的影响，相比传统估计方法，具有抗异常样本的能力，在海杂波数据样本包含少量大幅度的岛礁、目标回波情况下，仍然能够获得参数的高精度稳健估计。

3)由于本发明显式地给出双分位点估计表达式，相比已有的只能选择样本累计概率为0.5和0.75的双分位点估计方法，极大的扩大了样本累计概率的选取范围，提高了参数估计的灵活性与准确性。

附图说明

图1为本发明的实现流程图；

图2为用本发明和现有方法在不含异常样本的仿真杂波背景下进行参数估计性能比较结果示意图；

图3为用本发明和现有方法在含异常样本的仿真杂波背景下进行参数估计性能比较结果示意图。

具体实施方式

下面结合附图对本发明作进一步说明：

参照图1，本发明的实现步骤如下：

步骤1，获取杂波幅度递增序列。

雷达发射机发射连续的脉冲信号，脉冲信号照射到物体表面产生回波，雷达接收机接收回波数据，在回波数据中，选取n个杂波数据，对n个杂波数据进行取模并按升序排列，得到杂波幅度递增序列z1,z2,...,zt,...,zn，其中，zt表示杂波幅度递增序列中第t个杂波幅度，t＝1,2,...,n，本实例取n＝10⁴。

步骤2，确定广义帕累托分布的概率密度函数f(r)：

其中，r表示杂波的幅度，为概率密度函数的自变量，λ表示广义帕累托分布的形状参数，η表示广义帕累托分布的尺度参数。

步骤3，根据广义帕累托分布的概率密度函数f(r)，得到广义帕累托分布的累积分布函数f(r)：

步骤4，给定大于1的正数q，选取两个不同的样本累计概率α和β，并使得样本累计概率α和β满足：

本实例选取但不限于选取样本累计概率α＝0.5，当样本累计概率α＝0.5时，总是可以获得不错的估计性能。

步骤5，根据正数q的取值，得到分位点与广义帕累托分布参数的关系式。

5.1)根据分位点定义，得到表达式：

其中，rα表示样本累计概率为α时的分位点，rβ表示样本累计概率为β时的分位点；

5.2)根据样本累计概率间关系与5.1)中的表达式，进一步得到表达式：

其中，u表示中间变量。

5.3)根据正数q的取值,计算中间变量u；

5.3.1)当q为正整数且1＜q≤5时，利用多项式显示求根，计算中间变量u：

当q＝2，

当q＝3，

当q＝4，

其中，ψ表示中间变量，

当q＝5，表达式过长，对求唯一正根得到u；

5.3.2)当q＞5或q为小数时，选取迭代初始值u0∈(1,+∞)，利用迭代法，计算中间变量u：

其中，ui表示中间变量u的第i次迭代值，ui+1表示中间变量u的第i+1次迭代值；

5.4)利用中间变量u，得到分位点与广义帕累托分布形状参数λ和尺度参数η的关系式：

步骤6，利用杂波幅度递增序列z1,z2,...,zt,...,zn，计算每个分位点的估计值：

其中，sα表示分位点rα的估计值，sβ表示分位点rβ的估计值，表示杂波幅度递增序列中第n1个杂波幅度，表示杂波幅度递增序列中第n2个杂波幅度，round(nα)表示最接近nα的整数，round(nβ)表示最接近nβ的整数。

步骤7，根据分位点的估计值，得出广义帕累托分布的形状参数估计值和尺度参数估计值

7.1)根据正数q的取值，利用步骤6计算出的两个分位点的估计值sα和sβ分别代替步骤5.3)中的分位点rα和rβ，确定中间变量u的估计值

当q＝2，

当q＝3，

当q＝4，其中，表示中间变量ψ的估计值，

当q＝5，对求唯一正根得到

当q＞5或q为小数时，选取令利用迭代法

得到

其中，表示中间变量u的估计值的迭代初始值，表示中间变量u的估计值的第i次迭代值，表示中间变量u的估计值的第i+1次迭代值；

7.2)根据中间变量u的估计值得出广义帕累托分布的形状参数估计值和尺度参数估计值

下面结合仿真实验对本发明的效果做进一步说明。

仿真实验内容：

利用matlab软件仿真产生广义帕累托分布杂波数据。仿真实验中在同一杂波背景下分别采用本发明方法，二四阶矩估计，使用二分之一和一阶矩的分数阶矩估计和最大似然估计方法，得到广义帕累托分布的尺度参数和形状参数的估计。

利用估计得到的参数，通过相对均方根误差检验方法比较四种估计方法的结果，同时引入克拉美罗界。其中相对均方根误差的值越小，越接近克拉美罗界，表示估计误差越小，估计效果越好。

仿真实验1：仿真不含异常样本的纯杂波数据。

本实例取样本数n＝10⁴，尺度参数为1，样本累计概率α＝0.5，正整数q＝5，当形状参数从0.1至15变化时，进行参数估计，结果如图2所示，其中：

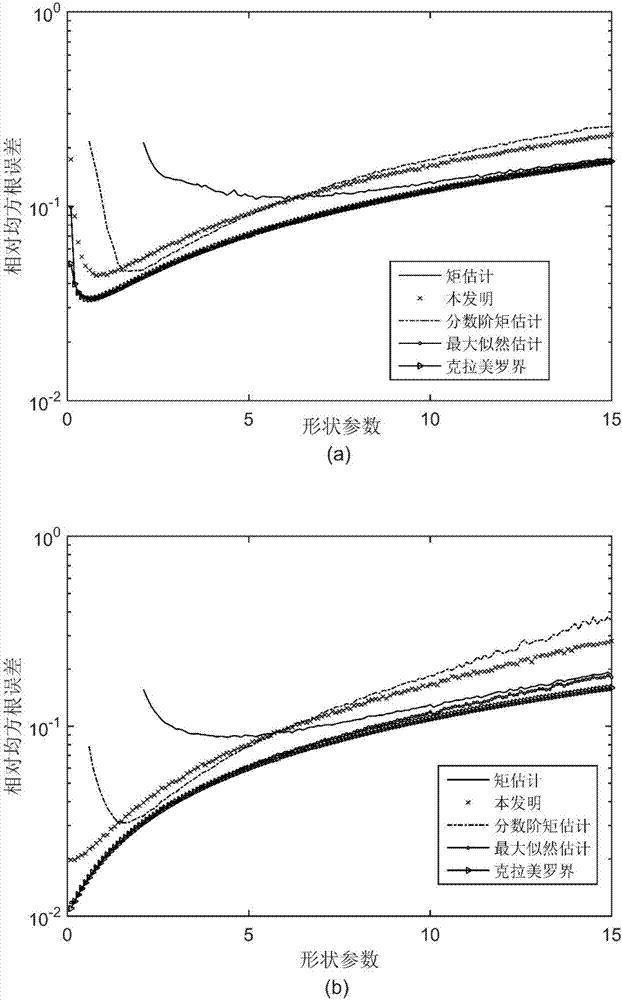
图2(a)为使用本发明和现有三种方法对不含异常样本的纯杂波数据进行尺度参数估计的相对均方根误差比较图，

图2(b)为使用本发明和现有三种方法对不含异常样本的纯杂波数据进行形状参数估计的相对均方根误差比较图；

图2中的横轴表示形状参数，纵轴表示估计性能衡量指标，其中，图2(a)与图2(b)的纵轴为相对均方根误差，图2中的框画线表示最大似然估计性能曲线，实线表示矩估计性能曲线，星画线表示本发明的性能曲线，点画线表示分数阶矩估计的性能曲线，三角形画线表示克拉美罗界。

从图2(b)可以看出，当形状参数小于1.53时，本发明优于分数阶矩估计；当形状参数大于1.53时，本发明效果稍差；当形状参数较小时，矩估计效果最差；当形状参数大于7时，矩估计效果迅速接近最大似然估计效果，这是因为此时形状参数较大，杂波接近高斯的。

图2(a)与图2(b)表明，无论形状参数取何值，最大似然估计的相对均方根误差几乎与克拉美罗界重合，性能近似最优，而二四阶矩估计，分数阶矩估计和本发明的方法得到的相对均方根误差相互交叉。但是，矩估计不能用于形状参数小于等于2的情况，分数阶矩估计不能用于形状参数小于等于0.5的情况，最大似然估计计算量过大。可见，在没有异常样本的情况下，本发明适用于重拖尾杂波的参数估计。

仿真实验2：仿真含异常样本的杂波数据

为体现实测杂波数据中存在由于岛礁等产生的异常散射单元，本实例仿真样本中异常单元的含量从0至2％随机选取，异常样本的幅度是杂波样本平均幅度的倍数，该倍数从至10中随机选取。

本实例取样本数n＝10⁴，尺度参数为1，样本累计概率α＝0.5，当形状参数从0.1至15变化时，进行参数估计，结果如图3所示，其中：

图3(a)为使用本发明分别取q＝3、q＝4、q＝5和现有三种方法对含异常样本的纯杂波数据进行尺度参数估计的相对均方根误差比较图，

图3(b)为使用本发明分别取q＝3、q＝4、q＝5和现有三种方法对含异常样本的纯杂波数据进行形状参数估计的相对均方根误差比较图；

图3中的横轴表示形状参数，纵轴表示估计性能衡量指标，其中，图3(a)与图3(b)的纵轴为相对均方根误差。

图3表明，由于异常样本的出现，矩估计、分数阶矩估计和最大似然估计的性能迅速下降，但是本发明仍然具有较好的性能，由图3还可看出，本发明中取q＝3的效果好于取q＝4和q＝5，进一步分析表明这与式1-(1-λ)^q接近1的程度有关。式1-(1-λ)^q越接近于1，本发明的准确性提高，但抗异常样本干扰能力下降。因此可以得出，当本发明用于实测海杂波环境时，正数q的选择应该是准确性与稳健性的折衷。