最小化机动车排放状况不确定性的尾气检测设备布点方法与流程

本发明涉及一种最小化机动车排放状况不确定性的尾气检测设备布点方法，属于公共设施选址技术领域。

背景技术：

机动车尾气排放是城市空气污染的一个主要来源，为减少交通路网上机动车尾气的污染物排放，希望可以尽早对在路机动车进行普查，筛选出高排放车辆，督促其车主进行维修或报废，从而减少路网上行驶的超标车辆数量，最终实现控制在路机动车尾气排放的目标。为实现这一目标，机动车尾气检测设备在路网上的布设位置就尤为重要。

关于机动车尾气检测设备布设位置的确定，申请号为201510214145.6和201611267877.2的发明专利已经公开了一些方法，包括目标为道路污染物浓度估计、道路信息缺乏情况下的尾气普查、特定种类机动车的检测等布点方法。

由于机动车尾气在路检测的最终目标是控制及减少道路尾气排放，而已有的布点方法虽然可以完成如道路污染物浓度估计、道路信息缺乏情况下的尾气普查、特定种类机动车检测的目标，却没有对如何减少道路尾气排放提出具体方法。

技术实现要素：

本发明技术解决问题：克服现有技术的不足之处，提供一种最小化机动车排放状况不确定性的尾气检测设备布点方法，可实现尽早对在路机动车进行普查的目标，从而尽早识别高排放车辆，通过督促高排放车辆车主对其进行维修或报废，减少路网上行驶的高排放车辆数量，最终减少交通路网上机动车尾气的污染物排放。

本发明技术解决方案：

一种最小化机动车排放状况不确定性的尾气检测设备布点方法，分为以下三个步骤：

步骤一：收集欲布点区域的交通路网路段、路径信息，以及每条路段的长度、交通流量信息；

步骤二：利用步骤一获取的路段、路径信息，以及每条路段的长度、交通流量信息，建立如下最小化机动车排放状况不确定性的尾气检测设备布点的数学模型：

s.t.

其中，a为交通网络g的路段集合，|a|表示a中的路段总数，a表示路段集合中的任一路段，la表示路段a的长度。p为交通路网上流量大于0的所有路径集合，|p|表示p中的路径总数，p表示路径集合中的任一路径，|p|表示路径p包含的路段总数，则p＝{ap，1，ap，2，…，ap，|p|}，(ap，1，ap，2，…，ap，|p|为路径p从其起点到终点依次经过的路段)，fp为路径p上的流量。预计布设的机动车尾气检测设备数量为m。

0-1变量xa和δpi：

路径p上的交通流所排放尾气的不确定性ep与流量fp成正比，与交通流的行驶距离dp成正比。即ep＝cfpdp，其中c表示不确定性系数。k是正整数，k＝1，2，…，i-1。i为路径p被截获的路段在p中的序号。

步骤三：求解步骤二所建立的最小化机动车排放状况不确定性的尾气检测设备布点的数学模型，最终xa等于1所对应的路段即为需布设机动车尾气检测设备的路段。

其中，求解最小化机动车排放状况不确定性的尾气检测设备布点的数学模型的算法如下：

步骤1.用1，2，…，|a|来表示集合a中的|a|个元素。令对任意a∈a，xa＝0；设机动车尾气检测设备的布点路段集合为l，令设路段集合a′，并令a′＝a。设循环次数t＝1。其中为空集。

步骤2.对集合a′中的任一元素j，j∈{1，2，…，|a′|}，若j不位于任何流量大于0的路径之上，则令a′＝a′\{j}。若则停止计算。

步骤3.选取集合a′中使得的值最大，且路段值最小的j*，令xj*＝1，l＝l∪{j*}，a′＝a′\{j*}，并令包含路段j*的路径流量为0，即若p∈pj*，则令fp＝0，其中pj*表示包含路段j*的路径集合。表示在路径p上路段ap，i的中点到路径终点的距离。

步骤4.判断l中元素个数|l|与m的大小关系，若|l|＜m，则令t自增1，转步骤2；若|l|＝m，则停止计算。

由上述算法可知，当或者布点路段数量达到m时，算法结束，此时xa等于1所对应的路段即为布设机动车尾气检测设备的路段，集合l即为需布设机动车尾气检测设备的路段集合。

本发明与现有技术相比的优点在于：本发明的最小化机动车排放状况不确定性的尾气检测设备布点方法，通过引入排放状况不确定性这一参数来衡量路段上因行驶超标车辆而造成的尾气污染程度。提出的模型最小化这种排放状况不确定性，因此如果在求解所得的路段集合上布设尾气检测设备，即可尽早识别高排放车辆，通过对这些高排放车辆进行维修或报废，最终达到减少交通路网上机动车尾气的污染物排放的目标。

附图说明

图1为本发明方法流程图；

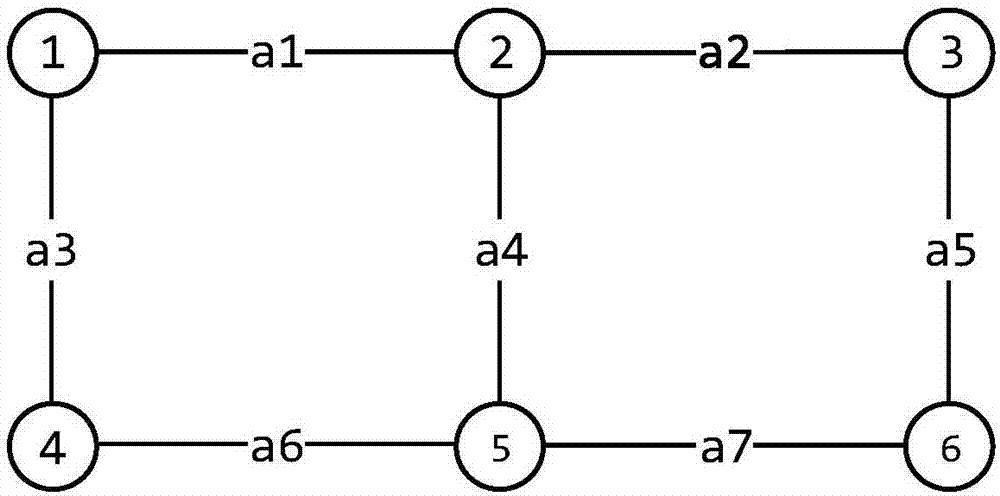
图2为一个交通网络示意图。

具体实施方式

下面结合实例对本发明作进一步描述，但本发明的保护范围并不限于此。

如图1所示，本发明具体实现如下：

步骤一：收集欲布点区域的交通路网路段、路径信息，以及每条路段的长度、交通流量信息；

步骤二：利用步骤一获取的路段、路径信息，以及每条路段的长度、交通流量信息，建立最小化机动车排放状况不确定性的尾气检测设备布点的数学模型：

首先，定义交通路网g(n，a)，其中n为交通网络的节点集合，a为交通网络的路段集合，|a|表示a中的路段总数，a表示路段集合中的任一路段，la表示路段a的长度。p为交通路网上流量大于0的所有路径集合，|p|表示p中的路径总数，p表示路径集合中的任一路径，|p|表示路径p包含的路段总数，则p＝{ap，1，ap，2，…，ap，|p|}，(ap，1，ap，2，…，ap，|p|为路径p从其起点到终点依次经过的路段)，fp为路径p上的流量。预计布设的机动车尾气检测设备数量为m。

定义0-1变量xa和δpi：

认为一辆未知尾气排放状况的机动车在道路上行驶，所排放的尾气量是有不确定性的，这种不确定性的原因是机动车可能是超标车辆所引起的。布设机动车尾气检测设备的目标就是最小化这种不确定性。而衡量这种不确定性，使用以下方法：路径p上的交通流所排放尾气的不确定性ep与流量fp成正比，与交通流的行驶距离dp成正比。即ep＝cfpdp，其中c表示不确定性系数。由于为了机动车尾气排放状况的有效测量，机动车尾气检测设备一般布设在路段上机动车可匀速行驶的位置，而非机动车需停车等待的靠近交叉路口的路段两端，因此我们假设，若某交通流在其行驶路径p′的路段ap′，i(i∈[1，|p′|])上被截获，则若某一路径p″在路网上未被任一检测设备截获，则对于该路径而言，dp″即为路径p″的起点到终点的距离，即

建立数学模型如下所示：

s.t.

(1)式中k是正整数，k＝1，2，…，i-1。i为路径p被截获的路段在p中的序号。

(1)式与如下形式等价：

其中，表示在路径p上路段ap，i的中点到路径终点的距离。

步骤三：求解步骤二所建立的最小化机动车排放状况不确定性的尾气检测设备布点的数学模型，最终xa等于1所对应的路段即为需布设机动车尾气检测设备的路段。

为求解所建立的最小化机动车排放状况不确定性的尾气检测设备布点的数学模型，提出如下算法，实现为：

步骤1.用1，2，…，|a|来表示集合a中的|a|个元素，令对任意a∈a，xa＝0；设机动车尾气检测设备的布点路段集合为l，令设路段集合a′，并令a′＝a，设循环次数t＝1；其中为空集；

步骤2.对集合a′中的任一元素j，j∈{1，2，…，|a′|}，若j不位于任何流量大于0的路径之上，则令a′＝a′\{j}，若则停止；

步骤3.选取集合a′中使得的值最大，且路段值最小的j*，令xj*＝1，l＝l∪{j*}，a′＝a′\{j*}，并令包含路段j*的路径流量为0，即若p∈pj*，则令fp＝0，其中pj*表示包含路段j*的路径集合，表示在路径p上路段ap，i的中点到路径终点的距离；

步骤4.判断l中元素个数|l|与m的大小关系，若|l|＜m，则令t自增1，转步骤2；若|l|＝m，则停止。

由上述算法可知，当或者布点路段数量达到m时，算法结束，此时xa等于1所对应的路段即为布设机动车尾气检测设备的路段，集合l即为需布设机动车尾气检测设备的路段集合。

为方便说明，这里选取一个简单的例子介绍本发明的具体过程。图2为一个交通网络示意图。该图中的路径有：p1＝(a1，a2，a5)、p2＝(a1，a4，a7)、p3＝(a3，a1，a2)、p4＝(a6，a4，a2)。路径流量分别为10、20、15、10。预计布设的机动车尾气检测设备数量m＝2。为方便计算，假设c＝1，每条路段的长度均为2。

1.令对任意a∈a＝{a1，a2，a3，a4，a5，a6，a7}，xa＝0；设机动车尾气检测设备的布点路段集合为l，令设路段集合a′，并令a′＝a＝{a1，a2，a3，a4，a5，a6，a7}。设循环次数t＝1。

2.集合a′中的任一元素均位于某条路径之上。

3.

选取其中最大的值所对应的路段即a1，令xa1＝1，l＝l∪{a1}＝{a1}，a′＝a′\{a1}＝{a2，a3，a4，a5，a6，a7}，并令包含路段a1的路径流量为0，即f1＝0，f2＝0。

4.此时|l|＝1＜m，因此令t＝2。

5.由于a5、a7不位于流量大于0的路径f3与f4之上，故令a′＝a′\{a5，a7}＝{a2，a3，a4，a6}。

6.

选取其中最大的值所对应的路段即a4，令xa4＝1，l＝l∪{a4}＝{a1，a4}，a′＝a′\{a4}＝{a2，a3，a6}，并令包含路段a4的路径流量为0，即f4＝0。

7.此时|l|＝2＝m，因此停止计算，得到xa等于1所对应的路段，a1和a4即为需布设机动车尾气检测设备的路段。

提供以上实施例仅仅是为了描述本发明的目的，而并非要限制本发明的范围。本发明的范围由所附权利要求限定。不脱离本发明的精神和原理而做出的各种等同替换和修改，均应涵盖在本发明的范围之内。