基于传感器网络的雷达信号频率估计方法与流程

本发明属于传感器网络分布式信息处理方法，特别涉及一种基于传感器网络的雷达信号频率估计方法。

背景技术：

在信号处理中，频率估计是常见的问题，因为频率估算的应用涵盖许多不同的领域，如语音和音频信号分析，雷达检测，生物医学工程，通信和电力交付。

在以前的研究工作中，学者们提出了各种各样的频率估计方法。在无噪声的信号方面，r.prony学者在文章‘实验和分析预测’中提出很容易通过其方法来确定频率。后来有学者在prony的工作基础上提出了在噪声情况下通过线性预测进行信号频率估计的方法。此外对于上述频率估计方法，自适应陷波滤波法已被广泛应用用于近年来的频率估计。自适应陷波滤波法为频率提供了一个灵活的框架估计。它能够跟踪具有时变频率的测量信号。频率估计的精度和鲁棒性方法在很多应用中都是至关重要的。频率由单个处理节点执行的估计具有一些缺点，如采样率不高足够的，采样时间有限，在噪音环境中，由单个节点执行的频率估计中，鲁棒性不够好。

在最近多年来，无线传感器网络已经变得非常受欢迎各种应用，如环境监控，医疗，信息收集，目标定位和等等。传感器节点形成传感器网络分布式，产生空间多样性，从而，不同的传感器节点收集不同环境的数据信息。在上述情况下，有理由用传感器网络提供一个有吸引力的低成本解来解决使用频率估计问题。将所有节点收集的数据传输到中央节点并以集中的方式处理数据通常由于沟通成本和鲁棒性而不予考虑。网络上的分布式估计由于其对节点和/或链路失败的灵活性和鲁棒性具有广泛的适用性。为此怎么将无线传感器网络应用于雷达信号频率估计中，且具有低成本、鲁棒性好、精度高等优点成为了研究的一个方向。

技术实现要素：

针对现有技术中的缺陷，本发明提供基于传感器网络的雷达信号频率估计方法，成本低、鲁棒性好、精确度高。

基于传感器网络的雷达信号频率估计方法，包括以下步骤：

s1：获取接收器接收到的雷达信号；

s2：建立陷波滤波模型；根据接收的雷达信号建立陷波滤波器的传递函数，并获得陷波滤波器的输出；

s3：建立传感器网络模型；建立包括多个传感器节点的传感器网络，传感器节点与其邻居共享数据，传感器中的每个节点网络均设有陷波滤波器；描述节点k处的陷波滤波器的输出，并结合邻居节点对输入信号的频率进行估计。

优选地，所述步骤s1中，所述接收的雷达信号xk[i]表示为：

其中，f为接收信号的频率，i为采样点序号，nk(i)为第i个接收信号中的噪声，a表示雷达信号的幅度，fs为采样频率，d(t)表示接受雷达信号中雷达与移动物体之间的距离，λ表示发送信号的波长。

优选地，所述步骤s2中，将接收的雷达信号xk[i]转换成离散正弦信号x[i]表示为：

x[i]＝asin(ω0ti+φ)+v(i)；

其中a,ω0,v(i),t分别对应表示幅度，角频率，初始相位，信号的高斯白噪声以及采样周期；fs为采样频率。

优选地，所述步骤s2中，陷波滤波器为iir滤波器，iir滤波器的传递函数描述为：

其中z为零点，p为极点，定义零点z的共轭零点z^*，极点p在z域的第四象限中的共轭极点p^*，a＝-2cos(ω0t)，ρ为小于1的参数；

iir滤波器的输出为：

优选地，所述步骤s3中，传感器网络包括n个传感器节点,节点k，k＝{1，...，n}，的邻居集合表示为nk；

在节点k处，输入信号的离散形式xk[i]描述为：

xk[i]＝aksin(ω0ti+φk)+vk(i)；

其中，ak，φk，vk(i)分别表示输入信号在节点k处的幅度，初始相位以及高斯白噪声；

节点k处的陷波滤波器的输出描述为：

将对频率估计转换为对参数a的估计。

优选地，所述步骤s3中，采用基于tls的分布式陷波滤波方法对输入信号的频率进行估计；即

其中，为第l个邻居节点对应时刻点接收信号的初始相位，clk为l个邻居节点对应时刻点的加权系数，

由上述技术方案可知，本发明提供的基于传感器网络的雷达信号频率估计方法，使用无线传感器网络分布式采样数据，并使用分布式陷波滤波方法处理估算频率。本发明提出基于传感器网络的分布式算法，基于分布式陷波滤波(dnf)的总体最小二乘法的dnf算法。该方法通信成本低、每个节点除了原始数据只与其邻居进行估计、鲁棒性好、精度高。

附图说明

为了更清楚地说明本发明具体实施方式或现有技术中的技术方案，下面将对具体实施方式或现有技术描述中所需要使用的附图作简单地介绍。在所有附图中，类似的元件或部分一般由类似的附图标记标识。附图中，各元件或部分并不一定按照实际的比例绘制。

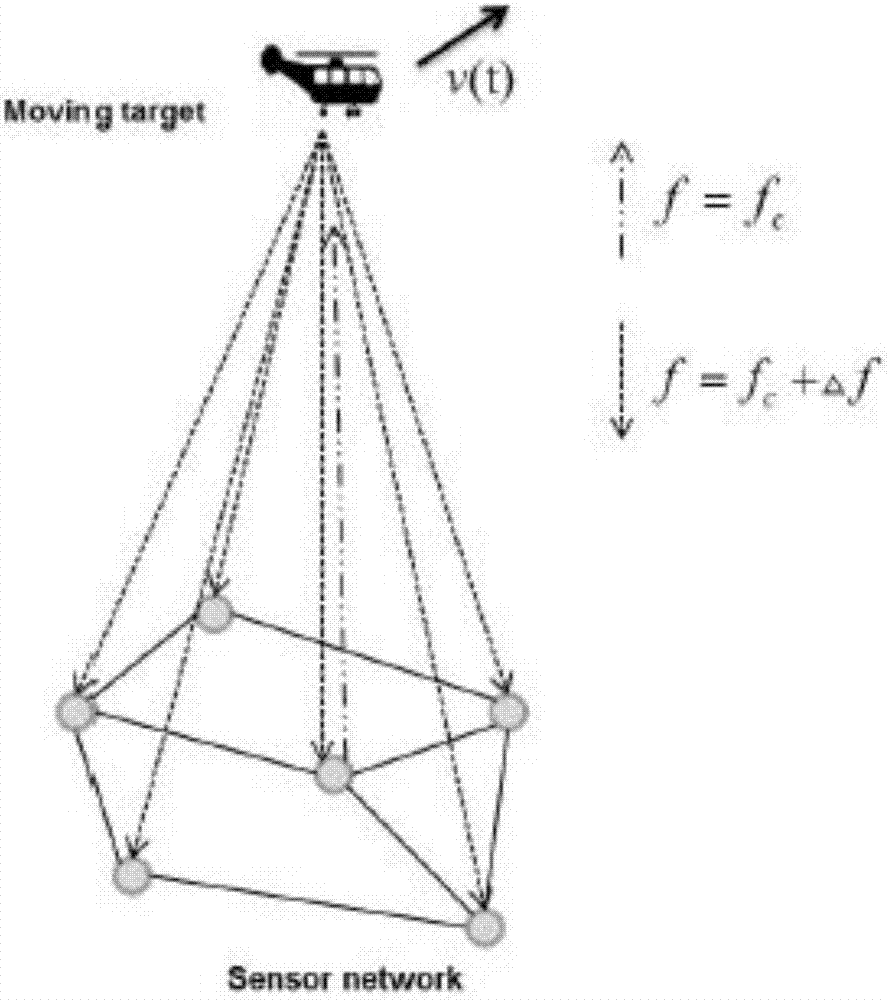
图1为雷达信号频率估计原理图。

图2为网络中nf-tls算法在雷达信号的频率估计中的emse图。

图3为用于雷达信号频率估计的dnf-tls算法的一致性表现图。

具体实施方式

下面将结合附图对本发明技术方案的实施例进行详细的描述。以下实施例仅用于更加清楚地说明本发明的技术方案，因此只作为示例，而不能以此来限制本发明的保护范围。需要注意的是，除非另有说明，本申请使用的技术术语或者科学术语应当为本发明所属领域技术人员所理解的通常意义。

实施例：

此前有学者提出了总最小二乘法(tls)方法用于频率估计。为此可以将分布式tls用于传感器网络陷波滤波频率估计，以多普勒雷达检测移动物体的运动的例子。当发射雷达信号被移动对象反射时并由接收器接收，因为多普勒效应所接收的信号可以与发送信号相比具有频移，频移被称为多普勒频移。此外，正多普勒频移意味着检测到的物体朝向雷达运动，而负多普勒频移的意思是物体正在从雷达移开。可以从来自多普勒频移的物体获得运动信息。为了简化问题，认为移动物体是一个移动点。

所考虑的多普勒雷达的发射信号表示为：

s(t)＝asin(2πfct)；

这里a和fc分别表示雷达信号的幅度和传输频率。然后，这个接收到的雷达信号可以描述为；

这里fd，d(t)，λ，δf，以及n(t)分别表示接受雷达信号的频率，相位函数，雷达与移动物体之间的距离，发送信号的波长，多普勒频移以及自适应高斯白噪声。根据多普勒效应原理，多普勒频移是与运动物体的径向速度成比例，可以表示为如下：

这里c和v(t)分别表示光速和移动物体径向速度。

如图1所示，雷达传感器网络设置在地面，而移动物体在空中。在网络中，让一个雷达(中央的一个是最好的)传输雷达信号，同时所有雷达传感器都接收到反射信号。假设移动目标和任何雷之间的距离达比在任何两个雷达传感器之间更长，因此频率不同雷达传感器接收的信号几乎相同。由雷达k接收的信号可以表示为：

通过应用频率滤波方法接收的雷达信号，可以获得仅包含多普勒频移目标信号，可以表达为：

抽样率应由奈奎斯特(nyquist)约束抽样法决定即满足fs＞2f0，这里根据上述条件，问题就变成了单频分布频率估计雷达信号通过传感器网络。因此，应用dnf-tls算法对这个问题是合理的。

1、陷波滤波模型：

描述观察到的离散正弦信号如下：

x[i]＝asin(ω0ti+φ)+v(i)(3)

这里a,ω0,v(i),t分别表示幅度，角频率，初始相位，信号的高斯白噪声以及采样周期。抽样率应由奈奎斯特(nyquist)约束抽样法决定即满足fs＞2f0，fs为采样频率，f0为最高频率。这里因此，离散信号包含原始的完整频率信息，可以从离散信号估计角频率ω0。

在信号处理中，通过使用陷波滤波器消除单频信号是很实际的属性。理想的陷波滤波器的传递函数在消除频率点的值为零，而它在任何其他频率点的值是1。数字陷波滤波器通常是iir滤波器(递归滤波器)。m阶iir数字滤波器的传递函数描述为：频率响应在零时达到最小值，在极点是无限的。因此，可以在适当的零和极设计需要的陷波滤波器。

在这里，考虑一个特殊情况，一个零点，称为z，是设在第一象限的单位圆上，一个极点，叫做p，设置在单位圆的直径上靠近z。为了避免传递函数中的复系数，必须设置零点z的共轭零点z^*和极点p在z域的第四象限中的共轭极点p^*。然后，可以获得陷波滤波器的传递函数：

这里a＝-2cos(ω0t)和ρ是一个小于且接近于1的参数。通过对(4)执行逆z变换，可以得到陷波滤波器的输出：

在(5)中，唯一的未知参数是a，可以通过估计a得到ω0。换句话说，将频率ω0估计问题变为估计参数a。

2、网络模型：

所考虑的传感器网络包括n个传感器节点,节点k，k＝{1，...，n}，的邻居集合表示为nk，分布在一些具有随机连接拓扑的地理区域。传感器节点可以通过链接与其邻居共享信息。节点k的邻居集合表示为nk，包括节点k。另外，传感器中的每个节点网络有一个陷波滤波器。

为了通过分布测量数据估计频率正弦信号x(t)＝asin(ω0t+φ)。在节点k处，观察到的离散信号可以描述为：

xk[i]＝aksin(ω0ti+φk)+vk(i)(6)

这里ak，φk，vk(i)分别表示在节点k观察信号的幅度，初始相位以及高斯白噪声。基于陷波滤波器模型，可以表达出来的在节点k处的陷波滤波器为：

然后，在考虑的传感器网络中，每个节点都能够与其邻居合作估计参数a。在考虑的传感器网络中，在每个时刻i，每个节点k可以访问输入离散信号xk(i)，并且每个陷波滤波器k产生输出yk(i)，其中xk(i)和yk(i)都是标量。可以通过自适应滤波算法估计(7)中的参数a。

考虑线性参数估计问题ax≈b，其中a是数据矩阵，b是观察值矢量，x是未知参数矢量。最小二乘法(ls)方法认为观测矢量数据矩阵是无噪声的。但是，总数最小二乘法(tls)方法考虑到观察矢量和数据矩阵是嘈杂的。ls方法通过最小化表示的平方残差的总和寻求未知参数向量x的估计，表达式如下：

而tls方法最小化加权平方和残差表示如下：

在考虑的传感器网络中，可以将(7)重写为：

为了使(8)更简单，将其重写为：

这里

在(9)式中，和都是噪声标量。因此，它是合理使用基于tls的算法来寻求估计的参数a。让和分别表示(9)中描述的线性系统的输出和理想输出。在节点k，理想输出表示为:

这里dk(i)＝0是在陷波滤波器k的理想输出。在传感器节点k定义局部代价函数为：

这里可以被计算出来，如下：

从(10)，传感器的瞬时局部代价函数在节点k表示为：

用于频率的dnf-tls算法的两步迭代估计可以描述为：

为第l个邻居节点对应时刻点接收信号的初始相位，clk为l个邻居节点对应时刻点的加权系数，μ为系数，这里梯度式为可以被计算出为如下：

在仿真中，让发送的频率雷达信号和移动物体的径向速度分别为30mhz和250m/s。然后，可以知道(1)的多普勒频移δf为50hz。所以感兴趣的参数是频率δf，让在(2)式中的λ为0。此外，采样率设置为300hz。因此，用于仿真的离散信号表示为：

xk[i]＝sin(2π×50×i/300)+nk(i)

还使用500个有序样本(i＝1,2,…,500)进行模拟。在这里，对于网络中的每个传感器节点还将学习步长设置为0.03。对于不同的试验，也随机选择参数a的不同初始值，其在[-1,0]内变化。

在这种仿真下，对比了学习曲线dnf-lms算法，集中式nf-lms算法，ncnf-lms算法，dnf-tls算法，集中式nf-tls算法和ncnf-tls算法。如图2，分布式算法稳态emse比相应的不合作算法要低得多。当比较分布式算法与相应的集中算法，他们之间的偏差emse在5db以内可以接受，此外，比较nf-tls算法相应的nf-lms算法，也可以看到nf-tls算法比相应的nf-lms算法实现了较低的稳态emse。一致性dnf-lms算法和dnf-tls算法的曲线如图3所示。图中的曲线说明了不同节点的稳态估计频率几乎相同，这表明了dnf-lms算法和dnf-tls算法在雷达信号的频率估计性能有很好的共识。根据获得的结果，dnf-tls算法用于雷达信号的频率估计是有效的。

在本发明中，基于自适应陷波滤波方法，提出了传感器网络频率估计dnf-tls算法。将新提出的算法应用于雷达信号频率估计实例。当输入数据和输出数据都是嘈杂的，dnf-tls算法比dnf-lms算法表现更好。总的来说，dnf-tls算法用于频率估计是有效的。

最后应说明的是：以上各实施例仅用以说明本发明的技术方案，而非对其限制；尽管参照前述各实施例对本发明进行了详细的说明，本领域的普通技术人员应当理解：其依然可以对前述各实施例所记载的技术方案进行修改，或者对其中部分或者全部技术特征进行等同替换；而这些修改或者替换，并不使相应技术方案的本质脱离本发明各实施例技术方案的范围，其均应涵盖在本发明的权利要求和说明书的范围当中。