一种摆线齿轮检测的误差补偿方法与流程

本发明涉及摆线齿轮检测，涉及由安装偏差所引起的检测误差补偿方案，具体涉及一种摆线齿轮检测的误差补偿方法。

背景技术：

摆线齿轮减速机因其具有传动比大、结构紧凑、效率高、运行平稳和寿命长的优良特性，广泛应用于机械、矿山、冶金、化工、纺织、国防工业等工业领域。摆线齿轮作为减速机中的一个核心部件，其制造精度直接影响整机性能。因此，对加工后的摆线齿轮零件的质量检测，已经成为整个生产过程的一个重要环节，任何一个细微的测量误差因素都会直接导致对产品质量的误判，因此，亟需一种误差补偿方法能够对由安装不当所引起的测量误差进行修正，从而得到能够反映零件加工质量的真实测量结果。

目前，常用的摆线齿轮齿廓检测是在三坐标测量仪上进行，由于摆线齿轮的装夹误差，摆线齿轮的轴心线与三坐标测量仪的z轴不能保证完全不重合，所以会产生对准误差从而影响对齿廊面的测量精度，但这种误差又是不可避免的。

在测量摆线齿轮齿廓偏差时，如图1，由于要测量齿廓面，先固定探头支架在z轴方向的位置，然后沿着y轴方向移动探头，并且绕z轴转动摆线齿轮，直到探头接触到摆线齿轮的齿廊面，读取测量点的坐标值，记录结果，然后再将摆线齿轮绕z轴等角度旋转，每转动一次，记录一次测量点的坐标值，直到摆线齿轮旋转一周，完成测量。在测量摆线齿轮的齿向偏差时，固定探头在y轴方向的位置，绕z轴转动摆线齿轮，直到探头接触到摆线齿轮，读取测量点的坐标值，记录结果，再将探头沿z轴方向，等距移动一定的距离，每移动一次，记录一次测量点的坐标值，直到探头沿摆线齿轮齿向移出，完成测量。但是，在上述实际测量过程中，装夹摆线齿轮总会有或多或少的偏差，例如，摆线齿轮轴心线的偏心和倾斜，这类偏差在实际测量过程中又是不可避免的，但由此引起的测量误差又会直接影响测量结果的准确性。

技术实现要素：

本发明的目的是提供一种对摆线齿轮检测的误差进行补偿的方法，以解决现有技术中测量偏差大的问题。鉴于此，本发明提出一种误差补偿修正方案：因为在三坐标测量仪下测得的摆线齿轮坐标，是摆线齿轮相对测量仪坐标系的位置，所以摆线齿轮轴心线的偏心其实就是它相对于测量仪坐标系原点的偏移，同理，摆线齿轮轴心线的倾斜可以看成轴心线绕各个坐标轴旋转后产生的。基于这种坐标变换的思路，就可以对摆线齿轮初始安装误差进行补偿，即首先得到摆线齿轮轴心线相对于原点的偏移量和旋转角度，再将坐标系相应的移动一定的距离和旋转一定的角度，就可以消除这种误差。

为了解决上述技术问题，本发明采用的技术方案是：

一种摆线齿轮检测的误差补偿方法，利用三坐标测量仪测量摆线齿轮进行测量，其特征在于，包括以下步骤：

步骤一、定义三坐标测量仪的x、y和z轴为原始坐标，利用三坐标测量仪测出摆线齿轮轴心线上不同高度方向的p(x1,y1,z1)和q(x2,y2,z2)两点坐标，利用公式(5)可得出摆线齿轮轴心线相对于x轴和y轴的偏转角度θ1和θ2，

其中，θ1为摆线齿轮轴心线相对于x轴偏转角度，θ2为摆线齿轮轴心线相对于y轴偏转角度；

步骤二、通过p(x1,y1,z1)和q(x2,y2,z2)两点坐标确定摆线齿轮轴心线方程，即为公式(6)，当z＝0时，公式(6)变为公式(7)，即可求出摆线齿轮轴心线与xoy平面交点坐标s(xs,ys)，其中，

步骤三、通过三坐标测量仪对摆线齿轮的齿廊面进行测量，得到测量值(xm,ym,zm)，测量的数据通过公式(3)进行转换得修正后的测量值(x,y,z)；

步骤四、然后将将原坐标系绕x,y轴旋转相应的角度和相对圆心移动相应的距离，修正后的测量值(x,y,z)通过经过公式(8)转换，得到补偿后的坐标值(xα,yα,zα)，即完成摆线齿轮齿廊面测量的补偿。

作为优选，在步骤三中，考虑探头半径对摆线齿轮的齿廊面测量影响，将经过公式(3)得到的修正值(x,y,z)通过公式(4)转换得到考虑探头半径大小的修正补偿值(xp,yp,zp)，

然后将(xp,yp,zp)通过公式(4)转换，得到补偿后的坐标值(xα,yα,zα)，即完成摆线齿轮齿廊面测量的补偿。

进一步的，上述测量用的三坐标测量仪以及测量补偿方法可应用于产品设计、模具装备、齿轮测量、叶片测量机械制造、工装夹具、汽模配件、以及电子电器的精密测量。

本发明的有益效果是：

本发明通过采用一种基于坐标转换的方法，通过误差补偿的方式，间接地消除了测量过程中由于装夹所引起的测量误差，从而满足对齿廊面高精度测量的要求，保证了摆线齿轮的生产质量。

附图说明

图1坐标系转换原理示意图。

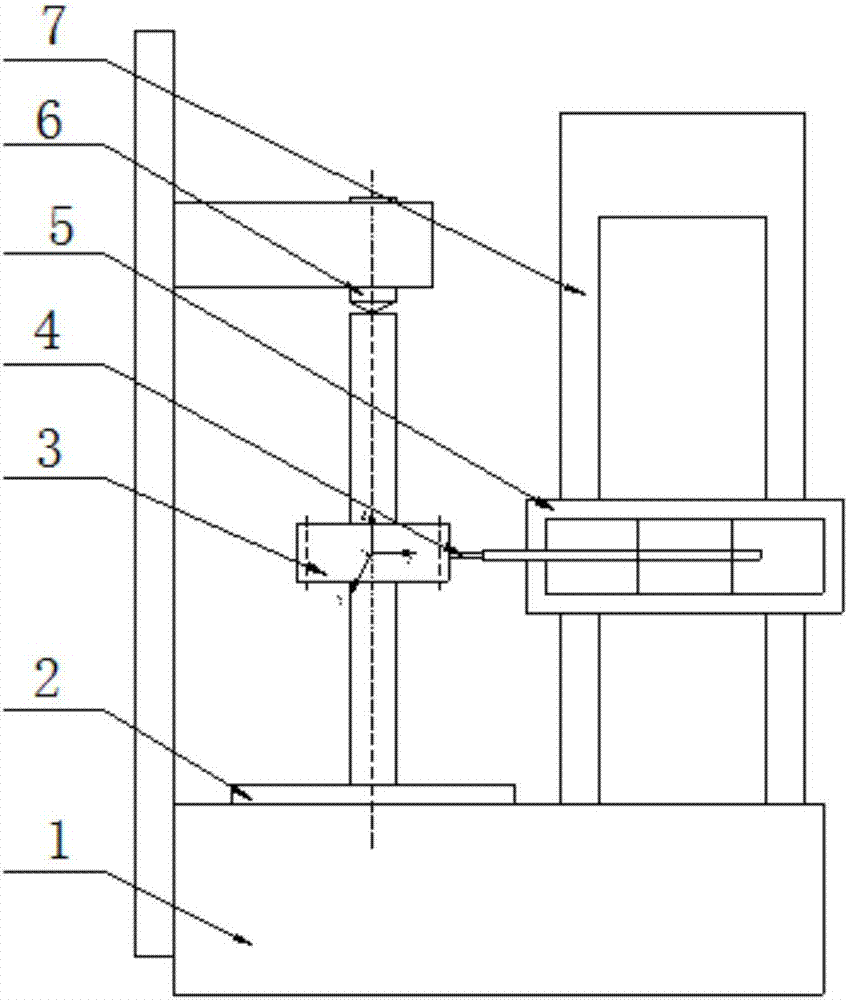
图2采用三坐标测量仪对摆线齿轮齿廓测量示意图。

图3摆线齿轮齿廊面方程生成结构示意图。

图4在倾斜和偏心情况下的摆线齿轮轴心线相对位置示意图。

1-基座，2-转台，3-摆线齿轮，4-探头，5-探头支架，6-顶针，7-滑座，8-轴心线。

具体实施方式

平面坐标转换实例

如图1所示，坐标系相对原点逆时针旋转θ角度，某点在未旋转坐标系下的坐标为a(x,y),旋转后的坐标系下坐标为b(x’,y’),同一个点在不同的坐标下具有不同的坐标值，显然它们之间的关系，是将两个坐标系连接起来的关键，通过计算，可以得到该点在两个坐标系下的关系式如下：

这样就实现了同一点在不同坐标系下的转化，点在二维坐标系下可以推导出这样关系，同理可以推导到三维坐标系也有类似的关系。

如图2所示，该结构包括：基座1、转台2、摆线齿轮3、探头4、探头支架5、顶针6、滑座7和轴心线8。

基座1起到支撑作用，摆线齿轮3的一端被安放在转台2上，另一端用顶针6固定,探头4安装在探头支架5上，探头支架5又安装在滑座7上，如图2所示：可以使得探头4在x,y,z方向上移动，以实现对摆线齿轮3齿廊面的测量。本发明提出了在测量摆线齿轮3齿廊面时，基于坐标系转换，探头4对准误差的一种补偿方案，探头4在测量摆线齿轮3齿廊面时，由于摆线齿轮3的轴心线8会相对原点有偏移，不仅如此，该轴心线8还会发生倾斜，这在测量的时候是不可避免的，对于摆线齿轮3这种高精度的传动齿轮而言，微小的误差都会影响它的测量精度，所以在测量时弥补这种因为测量时，摆线齿轮3的轴心线8的倾斜和偏心带来的误差就显得尤为重要。为了更好地解释补偿方案，先简单地介绍摆线齿轮3的齿廊面方程是如何生成的，如图3所示，滚圆圆心o1与基圆圆心o距离为a,滚圆由o1沿基圆o的外侧，做外切纯滚动运动到o2位置，相应地，滚圆上一点m1运动到点m，其中m1点的运动轨迹就是外摆线齿廓曲线，于是生成点m可以由(2)式表示：

在(2)式中，r1，r2分别表示基圆和滚圆的半径，是滚圆转动角度，l是生成点沿z轴的高度。当考虑到摆线齿轮3的轴心线8偏心和倾斜时，摆线齿轮3齿廊面模型可以由式3表示：

公式(3)中θ1，θ2分别表示，摆线齿轮3的轴心线8相对于x,y轴的偏转角，为摆线齿轮3齿廊面的测量值，为摆转齿轮轴心线8与xoy平面交点s(xs,ys,0)坐标，为考虑摆线齿轮3轴心线的偏心和倾斜，摆线齿轮3齿廊面的经过校正后的测量值，如果考虑到探头的半径大小，可将公式(3)变为式(4)，

在(4)式中，rμ表示探头半径的大小，n(nx,ny,nz)是摆线齿轮3的轴心线8在偏心和倾斜情况下的法线向量，(xp,yp,zp)为考虑探头半径大小后校正后的测量值。所以由(3)式可以得出，只要得出了摆线齿轮3的轴心线8相对于x,y轴的偏转角和轴心线相对圆心的偏移量就可以进行对准误差的补偿，通过公式(4)补偿后再通过公式(8)进行坐标系转换。

该方案为，如图4所示：用三坐标测量仪测得摆线齿轮3上面轴心的坐标p(x1,y1,z1)和下面轴心的坐标q(x2,y2,z2)，则轴心线相对于x轴和y轴的倾斜角度θ1，θ2可由公式(5)得出：

测出p和q这两点的坐标，则摆线齿轮3的轴心线8的空间直线方程就可以确立，即公式(6)，则在xoy平面内，z＝0,(6)公式可以改写为：

即可求出摆线齿轮3的轴心线8与xoy平面交点s(xs,ys,0)坐标，

其中，进而可以得出摆线齿轮3的轴心线8相对于原点的偏移量。

然后利用三坐标测量仪对摆线齿轮3的齿廊面进行测量得到(xm,ym,zm)，测量的坐标值根据公式(3)进行修正补偿，得到(x,y,z)，然后将将原坐标系绕x,y轴旋转相应的角度和相对圆心移动相应的距离。按公式(8)进行坐标转换，得到坐标系转换修正后齿廊面上测量点的坐标(xm,ym,zm)。

式中，rx和ry分别是绕x,y轴的旋转矩阵，t(δe)代表平移矩阵；

中(xm,ym,zm)是实际测量的摆线齿轮3齿廊面上测量点的坐标，最后一个是数字1；

中(xα,yα,zα)是坐标系转换修正后齿廊面上测量点的坐标，最后一个也是是数字1，因为描述空间三维变换的变换矩阵是4×4的形式，在矩阵的最后一行加上1，构成一个4×4的矩阵。每个测量点都要通过坐标转换得到修正后的测量值，从而达到消除倾斜角度和偏移的误差值。由于摆线齿轮3的轴心线8的偏移和倾斜是微量且不可避免的，在原始的坐标系中，这些误差在测量时会被显示出来，为了补偿这些偏差，可以将坐标系进行一定的反向“倾斜”和“偏心”处理，即是相应的旋转和偏移，来抵消摆线齿轮3的轴心线8的倾斜和偏心。这种思路其实是一种对象的转换，且它是可行的而又是方便操作的。使它的测量值达到理想值。