分布式光纤测温系统的降噪方法及装置与流程

本发明涉及光纤传感技术领域，特别涉及一种分布式光纤测温系统的降噪方法及装置。

背景技术：

分布式光纤测温系统(dts)的核心技术为光纤激光雷达技术，即利用激光器向光纤中注入激光脉冲，然后对其后向散射光进行采集、分析，就可以实时测得整根光纤沿线的温度变化。体现dts性能的指标主要包括空间定位精度、测温精度、空间分辨率、响应时间和传感距离等。尤其是测温精度和距离提升，一直是光纤传感技术的重点发展方向。

dts主要基于raman后向散射机理，采用anti-stokes光与stokes光的强度比来解调温度。但是raman散射信号十分微弱，需采用雪崩光电二极管进行光电转换，由于高反偏置和雪崩特性，引入了雪崩暗电流和附加噪声，使得光电转换后的信号噪声很大，导致实际采集到的anti-stokes光信号和stokes光信号完全无法分辨出信号细节，因此降噪是研制分布式光纤测温系统的关键环节，直接影响到系统的测温精度和传感距离。

若采用傅里叶变换在频域降噪，由于dts的噪声频谱是随机的，且背向散射信号的e指数函数的频谱也覆盖整个频域，因此很难在频域中将两者分离，效果无法保证。而小波变换作为多尺度分析工具，被誉为“信号显微镜”，能够自动调节信号分析的时宽和带宽，尤其适用于分布式光纤测温系统；所以，目前在分布式光纤测温系统中主要采用基于mallat算法的小波变换进行数据降噪处理。其特征在于，raman散射信号通常表现为低频信号或是一些比较平稳的信号，而噪声信号通常表现为高频信号，当对其进行小波变换时，信号的高频部分对应于高频小波系数，低频部分对应于低频小波系数，将包含噪声的信号进行小波变换后，用阈值法去除一定量的高频小波系数后，再做小波逆变换得到降噪后的信号。

在小波域做降噪处理效果是比较不错的。小波阈值降噪法计算简单且具有分析信号局部特征的能力，但是涉及到的阈值选取时比较困难，选取不当则对信号高频部分的损害较大，影响降噪效果。

技术实现要素：

基于此，本发明实施例的目的在于提供一种分布式光纤测温系统的降噪方法及装置，可以提高分布式光纤测温系统的降噪性能。

为达到上述目的，本发明实施例采用以下技术方案：

一种分布式光纤测温系统的降噪方法，包括：

采集光纤测温系统中的stokes光和anti-stokes光；

将stokes光和anti-stokes光分别转换成对应的电压；

对转换后的电压进行数据预处理；

对经过预处理的数据做提升小波变换，获得不同尺度下的小波系数；

为各尺度的高频小波系数构建隐马尔科夫树模型；

训练该隐马尔科夫树模型，求解该模型里面的各类参数；

根据所构建隐马尔科夫树模型，对含噪信号的高频小波系数做贝叶斯估计，得到一组真实信号高频小波系数；

通过估计出来的高频小波系数，结合最高尺度下的低频小波系数，做提升小波逆变换，完成信号重构，得到干净信号；

对干净信号再做预定数量的累加平均，得到最终信号。

优选地，在所述对转换后的电压进行数据预处理的步骤中，对转换后的电压进行累加平均2000次，提高系统信噪比。

优选地，在所述对干净信号再做预定数量的累加平均的步骤中，对干净信号做10次累加平均。

优选地，采用最大期望算法来求解该模型里面的各类参数。

本发明还提出一种分布式光纤测温系统的降噪装置，包括：

采集单元，用于采集光纤测温系统中的stokes光和anti-stokes光；

转换单元，用于将stokes光和anti-stokes光分别转换成对应的电压；

预处理单元，用于对转换后的电压进行数据预处理；

小波变换单元，用于对经过预处理的数据做提升小波变换，获得不同尺度下的小波系数；

模型建立单元，用于为各尺度的高频小波系数构建隐马尔科夫树模型；

训练单元，用于训练该隐马尔科夫树模型，求解该模型里面的各类参数；

估计单元，用于根据所构建隐马尔科夫树模型，对含噪信号的高频小波系数做贝叶斯估计，得到一组真实信号高频小波系数；

信号重构单元，用于通过估计出来的高频小波系数，结合最高尺度下的低频小波系数，做提升小波逆变换，完成信号重构，得到干净信号；

计算单元，用于对干净信号再做预定数量的累加平均，得到最终信号。

优选地，所述预处理单元对转换后的电压进行累加平均2000次，提高系统信噪比。

优选地，在所述计算单元中，对干净信号做10次累加平均。

优选地，所述训练单元采用最大期望算法来求解该模型里面的各类参数。

本发明提利用隐马尔可夫树模型反映了小波系数在尺度间的相关性，克服了阈值法对信号高频部分的不良影响，拥有更好的降噪效果。

附图说明

附图是用来提供对本发明的进一步理解，并构成说明书的一部分，与下面的具体实施方式一起用于解释本发明，但不应构成对本发明的限制。在附图中，

图1是分布式光纤测温系统的降噪方法的流程示意图；

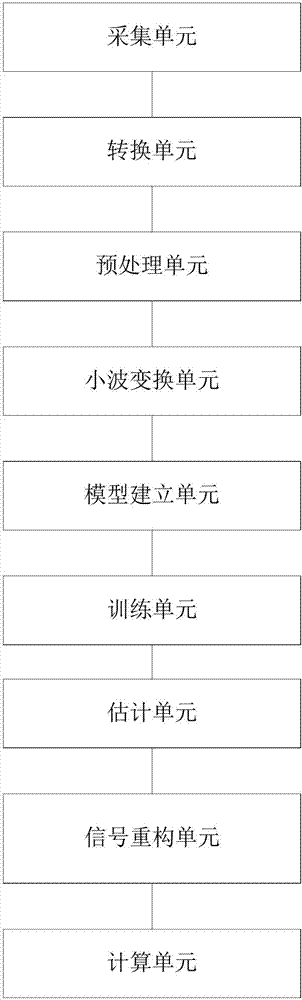
图2是分布式光纤测温系统的降噪装置的结构示意图；

图3是光纤测温系统的结构示意图。

具体实施方式

为使本发明的目的、技术方案及优点更加清楚明白，以下结合附图及实施例，对本发明进行进一步的详细说明。应当理解，此处所描述的具体实施方式仅仅用以解释本发明，并不限定本发明的保护范围。

本发明提出一种分布式光纤测温系统的降噪方法，其基于的光纤测温系统如图3所示，包括包括脉冲激光器、波分复用器、光电转换器、单模传感光纤、数据采集卡。其中，脉冲激光器与波分复用器的输入端相连，传感光纤与波分复用器的com(串行端口)端相连，波分复用器的两个输出端分别接双通道光电转换器的输入端，光电转换器的输出端分别连接到数据采集卡。脉冲激光器发出的脉冲光通过波分复用器进入传感光纤并进入测温现场，经测温现场沿传感光纤返回传输的散射光再进入波分复用器，经波分复用器中进行滤光输出stokes光和anti-stokes光，分别进入光电转换器将其转换成对应的电压，由数据采集卡完成a/d转换并将离散采样值传送至处理器，进行降噪处理。

本发明提出一种分布式光纤测温系统的降噪方法，其流程如图1所示，包括步骤：

s100、采集光纤测温系统中的stokes光和anti-stokes光；

s200、将stokes光和anti-stokes光分别转换成对应的电压；

s300、对转换后的电压进行数据预处理；

考虑到小波变换对于高频噪声的去噪效果非常好，但其在信噪比较低时去噪效果会降低，故在软件中先对数据做累加平均2000次，提高系统信噪比。累加2000次后,信号的强度增加2000倍,而噪声是随机的,它的强度只增加倍。因此，信噪比的增加为：倍。

s400、对经过预处理的数据做提升小波变换，获得不同尺度下的小波系数；

其中，提升小波正变换中，将含噪信号提升小波分解至j层，得到相应的提升小波分解系数wj,k。本发明中，考虑到分布式光纤测温系统具有一定的响应时间要求，经过多次实验，权衡运算量、能量紧致性等因素，小波基选取db4，分解层数(尺度)为4。

s500、为各尺度的高频小波系数构建隐马尔科夫树模型；

s600、训练该隐马尔科夫树模型，求解该模型里面的各类参数；

s700、根据所构建隐马尔科夫树模型，对含噪信号的高频小波系数做贝叶斯估计，得到一组真实信号高频小波系数；

在本发明中，经过分析发现，anti-stokes光的离散数据经提升小波分解得到的小波系数在同一尺度下呈现出尖峰、长拖尾的非gaussian分布的特征,这是由于小波系数具有持续性和聚集性造成的。另外，小波变换的二抽取过程使得小波系数随尺度增加依次减半，这便可以很自然的映射到树状结构上。综上，我们可为其构建隐马尔科夫树模型。hmt模型采用混合gaussian密度分布模型对小波系数的分布进行估计，隐状态变量的值决定了小波系数的大小，小波系数的持续性通过马尔科夫树中父节点及相邻节点和子节点的状态的相关性获得。为了方便anti-stokes光的数据分析,我们先做如下定义：

w表示一个小波系数的随机变量；s为w对应的具有2个可能状态(我们把小波系数分为两类，0为小值小波系数，1为大值小波系数)的隐状态随机变量,其概率分布函数psj(m)。对于给定状态s＝m,w的概率密度函数为均值为μm方差为σm的gaussian分布。而在具有2个可能状态时(0和1)，显然小波系数不能再仅由1个gaussian分布来描述，但可以用2个gaussian分布的加权和来近似(小值小波系数用小方差gaussian分布建模，大值小波系数用大方差gaussian分布建模，总分布用它俩的加权和近似)。另外，同一尺度下不同小波系数是具有相似统计特性的，考虑到可供训练anti-stokes光数据较少，为了简化问题，这里假设在同一尺度下所有小波系数有相同混合gaussian模型参数和状态转移概率，如此便可减少模型的参数数目，保证估计的稳定性。

所以，gaussian混合模型的随机变量w概率密度函数由2部分组成:隐状态随机变量s的概率分布函数和小波系数随机变量w的gaussian条件概率密度函数。

其中，为典型高斯分布公式。

在构建好的hmt模型中，每个小波系数wj由以下参数描述：

a、混合gaussian分布的均值和方差(j尺度下小波系数wj的状态为m时的均值和方差)；这里m＝{0,1}；0代表小值小波系数状态，1代表大值小波系数状态。

b、隐状态变量s的转移概率，当前为j尺度m状态，到(j+1)尺度n状态的转移概率(两个状态概率分布做乘积操作)；这里m,n＝{0,1}。

c、根节点的初始状态概率分布函数p(s＝m)，这里m＝{0,1}。

考虑到该模型的状态变量是隐藏的，只有观察到的小波系数作为训练数据，对于这种不完全数据的训练，我们采用期望最大算法(em)来计算模型参数。em算法是一种迭代算法。首先假定初始化一个包括均值、方差、状态转移概率及根节点的初始状态概率的hmt参数集θ0，在每一次迭代中，通过计算es[lnf(w，s|θ)|w，θ^l)](e步)并使之最大化(m步)并得到新的θ的估计θ^l+1，得到它的最优估计参数，从而找出和小波系数匹配最好的隐马尔科夫树模型。

假定x为源信号，且被加性gaussian噪声noise污染，观察到的含噪信号：y＝x+noise，注意x与noise是相互独立的。降噪的目标是从观察到的噪声信号y中获得对源信号x的估计x’。各信号对应的小波系数分别为wy，wx，wnoise，很明显，其中的wy服从混合高斯分布，wnoise服从高斯分布，由于提升小波变换的线性属性，独立高斯随机变量之和仍然服从高斯分布，且其方差为各变量方差之和，即有这里m＝{0,1}。

理论上噪声的小波系数wnoise的均值和方差与尺度无关，所以噪声是分布在各个尺度下的，但在最小尺度噪声能量最为集中，因此可用该尺度下信号的方差作为噪声方差的合理估计：

利用该最优hmt模型按照贝叶斯最小均方误差准则对含噪小波系数进行降噪处理，处理公式如下:

其中wj是观察到的含噪信号的小波系数，wj'是经降噪处理得到的源信号小波系数。jm表示hmt模型中节点隐状态，取值为{0,1}，是j尺度下的节点隐状态概率分布函数，是j尺度下节点状态为m的源小波系数概率密度函数方差，是最低尺度j下的噪声小波系数方差，由式(1)得到。和(观测到的小波系数wj对应的混合方差)都可由经过大量观测数据训练的hmt模型得到。

s800、通过估计出来的高频小波系数，结合最高尺度下的低频小波系数，做提升小波逆变换，完成信号重构，得到干净信号；

s900、对干净信号再做预定数量的累加平均，得到最终信号。

本发明提利用隐马尔可夫树模型反映了小波系数在尺度间的相关性，克服了阈值法对信号高频部分的不良影响，拥有更好的降噪效果。

优选地，在所述对转换后的电压进行数据预处理的步骤中，对转换后的电压进行累加平均2000次，提高系统信噪比。

优选地，在所述对干净信号再做预定数量的累加平均的步骤中，对干净信号做10次累加平均。

优选地，采用最大期望算法来求解该模型里面的各类参数。

本发明还提出一种分布式光纤测温系统的降噪装置，如图2所示，包括：

采集单元，用于采集光纤测温系统中的stokes光和anti-stokes光；

转换单元，用于将stokes光和anti-stokes光分别转换成对应的电压；

预处理单元，用于对转换后的电压进行数据预处理；

小波变换单元，用于对经过预处理的数据做提升小波变换，获得不同尺度下的小波系数；

模型建立单元，用于为各尺度的高频小波系数构建隐马尔科夫树模型；

训练单元，用于训练该隐马尔科夫树模型，求解该模型里面的各类参数；

估计单元，用于根据所构建隐马尔科夫树模型，对含噪信号的高频小波系数做贝叶斯估计，得到一组真实信号高频小波系数；

信号重构单元，用于通过估计出来的高频小波系数，结合最高尺度下的低频小波系数，做提升小波逆变换，完成信号重构，得到干净信号；

计算单元，用于对干净信号再做预定数量的累加平均，得到最终信号。

优选地，所述预处理单元对转换后的电压进行累加平均2000次，提高系统信噪比。

优选地，在所述计算单元中，对干净信号做10次累加平均。

优选地，所述训练单元采用最大期望算法来求解该模型里面的各类参数。

本发明与现有分布式光纤测温系统降噪方法相比具有如下优点：

1)有效降低了信号处理单元运算的时间和资源

在光纤测温技术领域普遍采用mallat卷积算法实现小波变换，然而这种算法运算量大，实时性不好，很不利于在硬件中实现。本发明采用sweldens提出的提升小波算法，由于其计算复杂度只有原来卷积算法的一半，有效节省了计算时间和资源，在硬件中实现也更加容易。

2)更好地把握了小波系数之间的本质特性及其相互关系，从而比阈值法拥有更好地降噪效果。

在光纤测温技术领域普遍采用的小波阈值降噪法，涉及到阈值选取时存在武断性，更重要的是在去噪的同时也会损失一部分有用信息，造成顾此失彼的局面，因此去噪效果还不是十分理想。究其原因是这种方法认为小波系数之间是统计独立、具有高斯分布性的，没有考虑系数之间的相关性。本发明提利用隐马尔可夫树状结构反映了小波系数在尺度间的相关性，克服了阈值法对信号高频部分的不良影响，拥有更好的降噪效果。

只要不违背本发明创造的思想，对本发明的各种不同实施例进行任意组合，均应当视为本发明公开的内容；在本发明的技术构思范围内，对技术方案进行多种简单的变型及不同实施例进行的不违背本发明创造的思想的任意组合，均应在本发明的保护范围之内。