基于迭代互耦校正的雷达协方差矩阵重构波束形成方法与流程

本发明属于共形阵天线波束形成技术领域，特别涉及一种基于迭代互耦校正的雷达协方差矩阵重构波束形成方法，适用于解决采样样本中期望信号功率较强导致自适应波束形成器稳健性下降的问题，以及考虑互偶效应时波束形成器性能下降的问题，并且在考虑阵元间互耦效应的同时改善了波束形成器的稳健性能。

背景技术：

共形阵列由于其具有电磁隐蔽性、大的扫描角度、小的负载重量及不干扰飞行体空气动力流场等优点而得到广泛的应用；然而，共形阵列波束形成技术在理论研究和开发应用方面都面临若干难题。首先，传统波束形成技术具有在实际环境中稳健性能不足的缺陷，这种缺陷应用到共形阵时依然存在；另外，阵列天线接收的信号在接收单元内部传输时，阵元间的互偶效应不容忽视。而共形阵复杂的阵元分布，加大了对其电磁特性进行精确分析和建模的难度，使得共形阵的互耦校正十分困难。故在充分发挥共形阵列优势的前提下，设计稳健的波束形成算法，突破互耦因素对波束形成器的限制是亟待解决的问题。

自适应波束形成技术的理论研究起始于20世纪60年代。1969年，capon提出最小方差无失真响应(mvdr)准则，该准则在保证期望信号增益的同时最小化阵列的输出功率，为波束形成器抑制干扰提供了理论基础。20世纪70年代，研究人员提出了采样矩阵求逆(smi)算法，该算法使用阵列接收信号快拍估计干扰加噪声协方差矩阵，能够自适应的抑制干扰信号。1974年，brennan等人推导出了smi波束形成算法的输出信干噪比的概率密度函数，给出了自适应算法的性能与训练样本数的关系。

在众多实际应用领域中，自适应波束形成器的性能会受到各种误差因素的影响，如信号观测误差，接收通道误差，阵元位置误差等，这些误差会造成阵列天线接收信号导向矢量失配，导致波束形成算法性能下降；而且当样本快拍中含有期望信号时，导向矢量的失配对自适应波束形成器的性能影响尤为显著。

在1991年，benjaminfriedlander和wanthonyj.weiss提出一种在阵元间存在互耦时的doa估计方法，可以较为准确的估计出信号的波达方向doa和均匀圆阵间的互耦，但是该在阵元间存在互耦时的doa估计方法在自适应波束形成技术领域没有应用；在2012年，gu提出了一种基于干扰加噪声协方差矩阵重构的波束形成方法，该方法利用重构后的协方差矩阵代替受到期望污染采样协方差矩阵来计算自适应权矢量，虽然在期望信号功率较强时具有较好的性能，但是该方法在实际应用中存在如下两个问题：第一，该方法要求阵列构型是精确已知的，唯一允许的误差是观测角误差，在考虑互偶效应时性能大幅度下降；第二，该方法在重构干扰加噪声协方差矩阵时计算复杂度很大，使得算法的实时性受到制约。

技术实现要素：

针对上述现有技术的不足，本发明的目的在于提出一种基于迭代互耦校正的雷达协方差矩阵重构波束形成方法，该种基于迭代互耦校正的雷达协方差矩阵重构波束形成方法对信号的入射角度和均匀圆阵的互耦矩阵进行迭代估计，结合干扰加噪声协方差矩阵重构方法，完成干扰加噪声协方差矩阵的重构和期望导向矢量的修正，得到一种在阵元存在互耦的条件下更加稳健的波束形成器。

为达到上述目的，本发明采用如下技术方案予以实现。

一种基于迭代互耦校正的雷达协方差矩阵重构波束形成方法，包括以下步骤：

步骤1，确定均匀圆阵，该均匀圆阵包括m个阵元，均匀圆阵设定范围内存在q个信号源，q个信号源向均匀圆阵发射q个入射信号，所述q个入射信号包含1个期望信号和q-1个干扰信号；

获取均匀圆阵的采样协方差矩阵r，并对所述均匀圆阵的采样协方差矩阵r进行特征分解，得到m个特征值；m、q分别为大于0的正整数，q>1，m表示均匀圆阵包括的阵元个数，与对均匀圆阵的采样协方差矩阵r进行特征分解后得到的特征值个数取值相等；

步骤2，计算入射方向为(θ,φ)的信号music谱，然后设定均匀圆阵的互耦矩阵初始值，进而得到q个入射信号的q个方位角初始值，分别为q∈{0,1,2,…,q-1}，表示第q+1个入射信号的方位角初始值；

初始化：令k表示第k次修正，k的初始值为1；令第k次修正后均匀圆阵的互耦矩阵为ck，并将q个入射信号的q个方位角初始值作为第0次修正后q个入射信号的方位角θ0；设定均匀圆阵的互耦矩阵初始值为c0，c0＝im，im表示m×m维单位矩阵；

步骤3，根据第k次修正后均匀圆阵的互耦矩阵ck对q个入射信号分别进行波达方向估计，得到第k次修正后入射方向为(θk,φ)的信号music谱pmusic(θk,φ)，以及第k次修正后q个入射信号的方位角；

步骤4，依次得到第k次修正后q个入射信号的music谱值倒数的和jck的定义式和计算式，进而计算得到第k次修正后均匀圆阵的互耦矩阵ck；

步骤5，令k加1，返回步骤3，直到jck-jc(k-1)<△，则修正迭代结束，jc(k-1)表示第k-1次修正后q个入射信号的music谱值倒数的和，△表示设定的门限值，并分别将修正迭代停止时对应的第k次修正后均匀圆阵的互耦矩阵ck，记为均匀圆阵的最终互偶矩阵将修正迭代停止时对应的第k次修正后q个入射信号的方位角，记为q个入射信号的最终方位角

步骤6，根据均匀圆阵的最终互偶矩阵和q个入射信号的最终方位角计算得到重构后均匀圆阵的干扰加噪声协方差矩阵

步骤7，计算得到期望信号的最终导向矢量为并根据重构后均匀圆阵的干扰加噪声协方差矩阵计算得到均匀圆阵的自适应波束形成器的权矢量为w，进而完成了基于迭代互耦校正的均匀圆阵干扰加噪声协方差矩阵重构的波束形成设计。

本发明的有益效果：第一，本发明使用doa与均匀圆阵互耦矩阵迭代估计的方法较为准确的估计出在互耦影响下的干扰加噪声协方差矩阵重构中不可或缺的两个参量，即均匀圆阵的互耦矩阵和干扰信号的方位角，使得干扰加噪声协方差矩阵的重构充分携带了互耦信息，提升了在互耦影响下的波束形成器的稳健性；第二，本发明采用在干扰角度区域取离散点而非积分的方法来重构干扰协方差矩阵，降低了计算复杂度，提高了算法的实时性。

附图说明

为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例或现有技术描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其他的附图。

图1为本发明的一种基于迭代互耦校正的雷达协方差矩阵重构波束形成方法流程图；

图2为互耦条件下存在观测误差时本发明方法性能随信噪比(snr)变化曲线图；

图3(a)为互耦条件下存在观测误差且输入信噪比为20db时本发明方法性能随样本数变化曲线图；

图3(b)为互耦条件下存在观测误差且输入信噪比为-5db时本发明方法性能随样本数变化曲线图；

图4为互耦条件下无观测误差时本发明方法性能随snr变化曲线图；

图5(a)为互耦条件下无观测误差且输入信噪比为20db时本发明方法性能随样本数变化曲线图；

图5(b)为互耦条件下无观测误差且输入信噪比为-5db时本发明方法性能随样本数变化曲线图。

具体实施方式

下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。

参照图1，为本发明的一种基于迭代互耦校正的雷达协方差矩阵重构波束形成方法流程图；其中所述基于迭代互耦校正的雷达协方差矩阵重构波束形成方法，包括以下步骤：

步骤1，确定均匀圆阵，该均匀圆阵包括m个阵元，获取均匀圆阵的采样协方差矩阵r，对所述均匀圆阵的采样协方差矩阵r进行特征分解，得到m个特征值；其中m为大于0的正整数。

具体地，确定均匀圆阵，该均匀圆阵包括m个阵元，均匀圆阵设定范围内存在q个信号源，q个信号源向均匀圆阵发射q个入射信号，所述q个入射信号包含1个期望信号和q-1个干扰信号；所述设定范围内为距离均匀圆阵s千米以内，s为大于0的正整数；本实施例中s取值为100。

q个入射信号相对于均匀圆阵的俯仰角为φ，φ＝{φ0,φ1,…,φq,…,φq-1}，q∈{0,1,…,q-1}，φq表示第q+1个入射信号相对于均匀圆阵的俯仰角，且φ0、φ1、…、φq、…、φq-1取值分别相等；φ0表示期望信号相对于均匀圆阵的俯仰角，q-1个干扰信号相对于均匀圆阵的俯仰角分别为φ1、φ2、…、φq-1。

获取均匀圆阵接收到的回波数据，并对所述均匀圆阵接收到的回波数据进行自相关处理，得到均匀圆阵的采样协方差矩阵r。

在已知期望信号个数为1、干扰信号个数为q-1，以及q个入射信号相对于均匀圆阵的俯仰角为φ的前提下，对均匀圆阵的采样协方差矩阵r进行特征分解，得到m个特征值；由于均匀圆阵的阵元个数为m，则经过特征分解后得到的特征值个数也为m。

对特征分解后得到的m个特征值进行从大到小排序，并分别将从大到小排序后的m个特征值中前q个特征值记为q个大特征值，将其余m-q个特征值记为m-q个小特征值；将前q个大特征值对应的特征向量，作为期望信号加干扰子空间，将m-q个小特征值对应的特征向量，记为噪声子空间，则对均匀圆阵的采样协方差矩阵r进行特征分解，其分解形式为：

其中，r为均匀圆阵的采样协方差矩阵，维数为m×m；λsi为q个大特征值分别为对角元素形成的对角矩阵，usi为q个大特征值对应的特征向量形成的期望信号加干扰子空间，λn为m-q个小特征值分别为对角元素形成的对角矩阵，un为m-q个小特征值对应的特征向量形成的噪声子空间，上标h表示共轭转置操作，m、q分别为大于0的正整数，m>q；m表示均匀圆阵包括的阵元个数，与对均匀圆阵的采样协方差矩阵r进行特征分解后得到的特征值个数取值相等。

步骤2，计算入射方向为(θ,φ)的信号music谱，然后设定均匀圆阵的互耦矩阵初始值，则入射方向为(θ,φ)的信号music谱就有了一个初始估计值；将均匀圆阵的互耦矩阵初始值代入入射方向为(θ,φ)的信号music谱pmusic(θ,φ)表达式中，并在设定方位角范围内搜索music谱峰，进而得到q个入射信号的q个方位角初始值，分别为

具体地，所述入射方向为(θ,φ)的信号music谱pmusic(θ,φ)，其表达式为：

其中，θ表示q个入射信号的方位角，φ表示q个入射信号相对于均匀圆阵的俯仰角，a(θ,φ)为入射方向为(θ,φ)的信号导向矢量，c为均匀圆阵的互耦矩阵，且均匀圆阵的互耦矩阵c是未知的；un为m-q个小特征值对应的特征向量形成的噪声子空间，上标h表示共轭转置操作。

设定均匀圆阵的互耦矩阵初始值c0，c0＝im，im表示m×m维单位矩阵；将均匀圆阵的互耦矩阵初始值c0代入入射方向为(θ,φ)的信号music谱pmusic(θ,φ)表达式中，并在0°到180°方位角范围内搜索music谱峰，进而得到q个入射信号的q个方位角初始值，分别为表示第q+1个入射信号的方位角初始值；其中，设定方位角范围内为0°到180°范围内。

初始化：令k表示第k次修正，k的初始值为1；并将q个入射信号的q个方位角初始值作为第0次修正后q个入射信号的方位角θ0；设定均匀圆阵的互耦矩阵初始值为c0，c0＝im，im表示m×m维单位矩阵。

步骤3，特征分解完成后，在考虑均匀圆阵互耦的情况下，令第k次修正后均匀圆阵的互耦矩阵为ck，并根据第k次修正后均匀圆阵的互耦矩阵ck使用music谱估计方法对q个入射信号分别进行波达方向(doa)估计，得到第k次修正后入射方向为(θk,φ)的信号music谱pmusic(θk,φ)。

具体地，在考虑均匀圆阵互耦的情况下，根据第k次修正后均匀圆阵的互耦矩阵ck使用music谱估计方法对入射的期望信号和q-1个干扰信号进行波达方向(doa)估计，计算得到第k次修正后入射方向为(θk,φ)的信号music谱pmusic(θk,φ)，其表达式为：

其中，θk表示第k次修正后q个入射信号的方位角，φ表示q个入射信号相对于均匀圆阵的俯仰角，a(θk,φ)为入射方向为(θk,φ)的信号导向矢量，ck为第k次修正后均匀圆阵的互耦矩阵，且第k次修正后均匀圆阵的互耦矩阵是未知的；un为m-q个小特征值对应的特征向量形成的噪声子空间，上标h表示共轭转置操作。

由于第k次修正后均匀圆阵的互耦矩阵c是未知的，入射方向为(θk,φ)的信号music谱pmusic(θk,φ)无法计算，那么期望信号和干扰信号的波达方向(doa)就是未知的。

在设定方位角范围内搜索第k次修正后入射方向为(θk,φ)的信号music谱pmusic(θk,φ)的music谱峰，得到第k次修正后q个入射信号的方位角为θk，θk＝{θ0k,θ1k,…,θqk,…,θ(q-1)k}，q∈{0,1,…,q-1}，θqk表示第k次修正后第q+1个入射信号的方位角；θ0k表示第k次修正后期望信号的方位角，θ1k,θ2k,…,θ(q-1)k为第k次修正后q-1个干扰信号的方位角；其中，设定方位角范围内为0°到180°范围内。

步骤4，定义第k次修正后q个入射信号的music谱值倒数的和为jck，由步骤3可知，当第k次修正后均匀圆阵的互耦矩阵与实际的均匀圆阵的互耦矩阵取值相等，则第k次修正后q个入射信号的music谱值倒数的和jck具有最小值；如果第k次修正后均匀圆阵的互耦矩阵与实际的均匀圆阵的互耦矩阵取值不相等，则第k次修正后q个入射信号的music谱值倒数的和jck没有最小值；那么在已经得到第k次修正后q个入射信号的q个方位角情况下，让第k次修正后q个入射信号的music谱值倒数的和jck取值最小，进而计算得到第k次修正后均匀圆阵的互耦矩阵ck。

步骤4具体包括如下子步骤：

(4a)根据第k次修正后均匀圆阵的互耦矩阵ck，定义第k次修正后q个入射信号的music谱值倒数的和为jck，其定义表达式为：

其中，表示入射方向为的信号导向矢量，φq表示第q+1个入射信号相对于均匀圆阵的俯仰角，表示第k次修正后第q+1个入射信号的方位角，||||²表示取模值之后再求平方操作；ck为第k次修正后均匀圆阵的互耦矩阵，un为m-q个小特征值对应的特征向量形成的噪声子空间，上标h表示共轭转置操作。

则由步骤3可知，当设定的均匀圆阵的互耦矩阵初始估计值与实际的均匀圆阵的互耦矩阵取值不相等，则第k次修正后q个入射信号的music谱值倒数的和jck没有最小值；那么在已经得到第k次修正后q个入射信号的q个方位角估计值的情况下，让第k次修正后q个入射信号的music谱值倒数的和取值最小，来修正均匀圆阵的互耦矩阵，即求解第k次修正后q个入射信号的music谱值倒数的和jck取值最小时对应的第k次修正后均匀圆阵的互耦矩阵。

(4b)由于均匀圆阵的互耦矩阵具有一些特殊的性质：第一，均匀圆阵的互耦矩阵是一个对称矩阵；第二，均匀圆阵相邻两阵元相距的距离越大，彼此之间的互阻抗就越小；第三，均匀圆阵闭合的几何结构，即编号为2的阵元对编号为1的阵元的互阻抗，与编号为1的阵元对编号为2的阵元的互阻抗取值相等。

基于以上特性，第k次修正后均匀圆阵的互耦矩阵ck是一个复循环对称矩阵，可以由第k次修正后均匀圆阵的互耦矩阵ck第一行中的前lc个元素完全确定，表示向下取整操作；并且确定第k次修正后均匀圆阵的互耦矩阵ck与入射方向为(θk,φ)的信号导向矢量a(θk,φ)的乘积，等价于入射方向为(θk,φ)的信号导向矢量a(θk,φ)中的m个元素组成的m×lc维矩阵q[a(θk,φ)]与第k次修正后均匀圆阵的互耦矩阵ck中第一行的前lc个元素完组成的lc×1维向量ck的乘积，即cka(θk,φ)＝q[a(θk,φ)]ck。

其中，ck为第k次修正后均匀圆阵的互耦矩阵ck中第一行的前lc个元素组成的lc×1维向量，cdk表示第k次修正后均匀圆阵的互耦矩阵ck中第一行的第d+1个元素，上标t表示转置操作。

入射方向为(θk,φ)的信号导向矢量a(θk,φ)中的m个元素组成的m×lc维矩阵q[a(θk,φ)]由第k次修正后的第一m×lc维矩阵q1k、第k次修正后的第二m×lc维矩阵q2k、第k次修正后的第三m×lc维矩阵q3k和第k次修正后的第四m×lc维矩阵q4k相加得到，即q[a(θk,φ)]＝q1k+q2k+q3k+q4k，第k次修正后的第一m×lc维矩阵q1k、第k次修正后的第二m×lc维矩阵q2k、第k次修正后的第三m×lc维矩阵q3k和第k次修正后的第四m×lc维矩阵q4k分别由入射方向为(θk,φ)的信号导向矢量a(θk,φ)中的元素构成，其中第k次修正后的第一m×lc维矩阵q1k中第r行、第h列元素为q1(r,h)k，第k次修正后的第二m×lc维矩阵q2k中第r'行、第h'列元素为q2(r',h')k，第k次修正后的第三m×lc维矩阵q3中第r”行、第h”列元素为q3(r”,h”)k，第k次修正后的第四m×lc维矩阵q4中第r”'行、第h”'列元素为q4(r”',h”')k，表达式分别为：

其中，r∈{1,2,…,row1k}，h∈{1,2,…,col1k}，row1k表示第k次修正后的第一m×lc维矩阵q1k的行数，col1k表示第k次修正后的第一m×lc维矩阵q1k的列数，r'∈{1,2,…,row2k}，h'∈{1,2,…,col2k}，row2k表示第k次修正后的第二m×lc维矩阵q2k的行数，col2k表示第k次修正后的第二m×lc维矩阵q2k的列数，r”∈{1,2,…,row3k}，h”∈{1,2,…,col3k}，row3k表示第k次修正后的第三m×lc维矩阵q3k的行数，col3k表示第k次修正后的第三m×lc维矩阵q3k的列数，r”'∈{1,2,…,row4k}，h”'∈{1,2,…,col4k}，row4k表示第k次修正后的第四m×lc维矩阵q4k的行数，col4k表示第k次修正后的第四m×lc维矩阵q4k的列数，表示向上取整操作；a(θk,φ)r+h-1表示入射方向为(θk,φ)的信号导向矢量a(θk,φ)中第r+h-1个元素，a(θk,φ)r'-h'+1表示入射方向为(θk,φ)的信号导向矢量a(θk,φ)中第r'-h'+1个元素，a(θk,φ)m+1+r”-h”表示入射方向为(θk,φ)的信号导向矢量a(θk,φ)中第m+1+r”-h”个元素，a(θk,φ)r”'+h”'-m-1表示入射方向为(θk,φ)的信号导向矢量a(θk,φ)中第r”'+h”'-m-1个元素；θk表示第k次修正后q个入射信号的方位角，且第0次修正后q个入射信号的方位角θ0为q个入射信号的q个方位角初始值。

(4c)由(4b)所描述的均匀圆阵的互耦矩阵性质可以得到，第k次修正后的均匀圆阵的互耦矩阵ck与入射方向为的信号导向矢量可以进行等价代换，即其中，ck为第k次修正后均匀圆阵的互耦矩阵ck的第一行的前lc个元素组成的lc×1维向量；进而计算得到第k次修正后q个入射信号的music谱值倒数和jck，其计算表达式为：

其中，||||²表示取模值之后再求平方操作。

(4d)为了求解第k次修正后均匀圆阵的互耦矩阵ck的第一行的前lc个元素组成的lc×1维向量ck，添加一个线性约束，假设均匀圆阵的互偶矩阵的阵元内部自阻抗为1，则ck(1,1)＝1，即e^hck＝1，其中e为首元素为1、其余元素均为0的l×1维向量，即建立如下方程：

其中，上标h表示共轭转置操作，s.t.表示约束条件。

最后计算得到第k次修正后均匀圆阵的互耦矩阵ck的第一行的前lc个元素组成的lc×1维向量ck，其表达式为：

ck＝gk^-1e(e^hgk^-1e)^-1

由于第k次修正后均匀圆阵的互耦矩阵ck的第一行的前lc个元素组成的lc×1维向量ck为第k次修正后均匀圆阵的互耦矩阵ck的第一行的前lc个元素组成的lc×1维向量，且第k次修正后均匀圆阵的互耦矩阵ck为一个复循环对称矩阵，故第k次修正后均匀圆阵的互耦矩阵ck中的元素可以由第k次修正后均匀圆阵的互耦矩阵ck的第一行的前lc个元素组成的lc×1维向量ck中元素完全确定。

因此，根据第k次修正后均匀圆阵的互耦矩阵ck的第一行的前lc个元素组成的lc×1维向量ck，计算得到第k次修正后均匀圆阵的互耦矩阵ck。

步骤5，令k加1，返回步骤3，直到jck-jc(k-1)<△，则修正迭代结束，jc(k-1)表示第k-1次修正后q个入射信号的music谱值倒数的和，△表示设定的门限值，本实施例中△取值为0.0001；并分别将修正迭代停止时对应的第k次修正后均匀圆阵的互耦矩阵ck，记为均匀圆阵的最终互偶矩阵将修正迭代停止时对应的第k次修正后q个入射信号的方位角θk，记为q个入射信号的最终方位角表示经过修正后第q+1个入射信号的最终方位角；进而得到q个入射信号的q个最终入射方向，分别为φq表示第q+1个入射信号相对于均匀圆阵的俯仰角；其中，为期望信号的最终入射方向。

步骤6，在已经获得q个入射信号的q个最终入射方向和均匀圆阵的最终互偶矩阵后开始进行均匀圆阵的干扰加噪声协方差矩阵重构；其中包括均匀圆阵的干扰协方差矩阵重构和均匀圆阵的噪声协方差矩阵重构；进而计算得到重构后均匀圆阵的干扰加噪声协方差矩阵。

步骤6具体包括如下子步骤：

(6a)从q个入射信号的q个最终入射方向中剔除期望信号的最终入射方向中，获取q-1个干扰信号的最终入射方向，分别为

考虑到谱估计算法的误差，设定方位角估计误差范围为△θ，这样q-1个干扰信号角度区域可以表示为

即q-1个干扰信号的最终入射方向都位于内，且q-1个干扰信号角度区域包含q-1个离散采样点，每个离散采样点分别对应一个干扰信号的最终入射方向；在q-1个干扰信号角度区域内任意选取l'个离散采样点计算协方差矩阵，l'≤q-1，再进行求和得到重构后均匀圆阵的干扰协方差矩阵即

其中，∪表示求并集操作，b(θl',φl')为q-1个干扰信号角度区域内第l'个离散采样点处的导向矢量，l'＝1,2,…,l'，又根据q个入射信号的q个最终入射方向和均匀圆阵的最终互偶矩阵计算得到经过互耦校正后期望信号的导向矢量b(θ,φ)，故计算得到重构后均匀圆阵的干扰协方差矩阵其表达式为：

其中，r表示均匀圆阵的采样协方差矩阵，b(θl',φl')表示q-1个干扰信号角度区域内第l'个离散采样点处的导向矢量，与入射方向为(θl',φl')的信号导向矢量取值相等；进而完成均匀圆阵的干扰协方差矩阵重构。

(6b)进行均匀圆阵的噪声协方差矩阵重构，在理想状态下，对均匀圆阵的采样协方差矩阵进行特征分解后得到的m-q个小特征值分别相等，其值就是噪声功率值。

但在实际情况中，m-q个小特征值是不相等的，为了计算简便，在m-q个小特征值选取特征值最小值，作为均匀圆阵的噪声功率估计值进而计算得到重构后均匀圆阵的噪声协方差矩阵i表示m×m维单位矩阵。

(6c)进行均匀圆阵的干扰加噪声协方差矩阵重构：根据重构后均匀圆阵的干扰协方差矩阵和重构后均匀圆阵的噪声协方差矩阵计算得到重构后均匀圆阵的干扰加噪声协方差矩阵其表达式为：

其中，r表示均匀圆阵的采样协方差矩阵，i表示m×m维单位矩阵；进而完成了均匀圆阵的干扰加噪声协方差矩阵重构。

步骤7，计算得到期望信号的最终导向矢量为并根据重构后均匀圆阵的干扰加噪声协方差矩阵利用线性约束最小方差(lcmv)准则计算得到均匀圆阵的自适应波束形成器的权矢量为w，进而完成了基于迭代互耦校正的均匀圆阵干扰加噪声协方差矩阵重构的波束形成设计。

具体地，计算得到期望信号的最终导向矢量为为入射方向为的信号导向矢量，为期望信号的最终入射方向，则利用线性约束最小方差(lcmv)准则求出均匀圆阵的自适应波束形成器的权矢量w，其表达式为：

其中，上标-1表示求逆操作，上标h表示共轭转置操作；进而完成了基于迭代互耦校正的均匀圆阵干扰加噪声协方差矩阵重构的波束形成设计。

通过以下仿真实验对本发明效果作进一步验证说明。

(一)仿真条件

本发明的仿真实验在matlab软件下进行的，在本发明的实验中，均匀圆阵采用10个阵元，q个入射信号的信号波长设置为0.1米，相邻阵元间距d与q个入射信号的信号波长的比值d/λ的为0.5，每个入射信号相对于均匀圆阵的俯仰角均设置为30°，期望信号的方位角设置为95°，设置两个干扰信号，两个干扰信号的方位角分别为50°和140°。

具体的算法参数如下表所示：

(二)仿真内容和结果分析

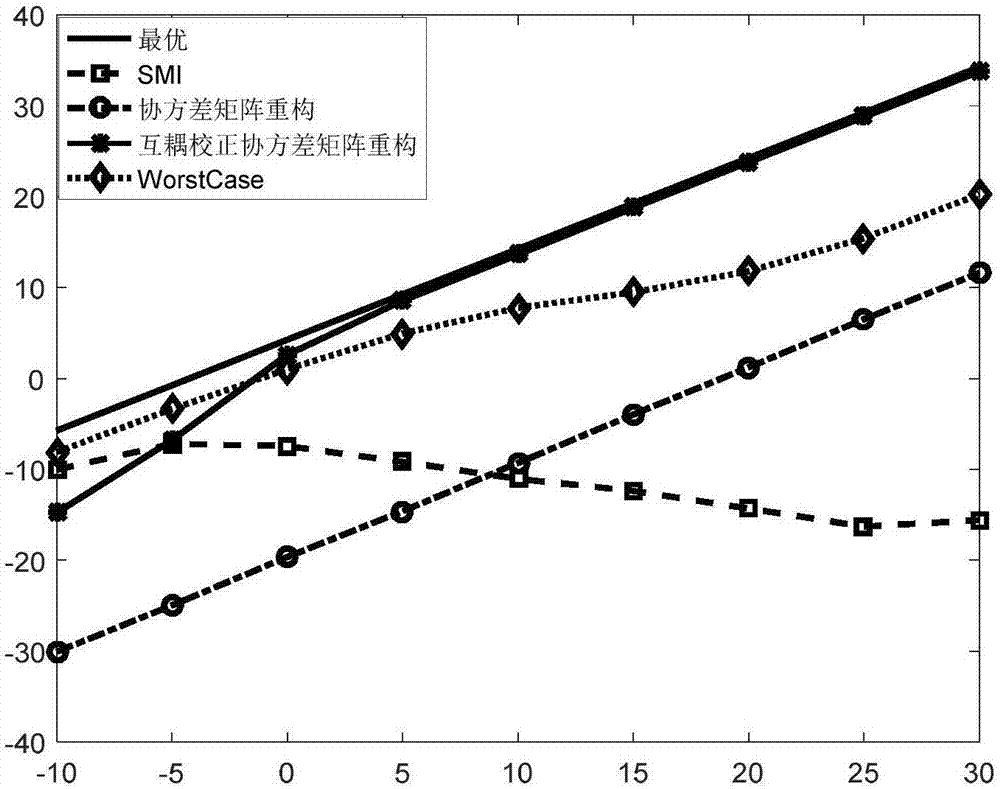
为了说明本发明算法的优越性，图2到图5给出了其他几种波束形成算法的处理结果，包括最优波束形成器，采样矩阵求逆(smi)波束形成器，协方差矩阵重构算法和最差性能最优化方法。

图2的横轴表示输入信噪比，纵轴表示输出信干噪比；图2表示存在信号观测误差，采样快拍数为30，几种波束形成方法的输出信干噪比随期望信号输入信干噪比变化的曲线。从图2中我们可以看到，在同时存在互耦影响和入射信号观测误差的情况下，普通协方差矩阵重构方法性能急剧下降，在低信噪比的场景中性能甚至远远不如smi方法；最差性能最优化波束形成方法保有较好的性能稳健性，但是在期望信号功率变强时其性能与理论最优值的差距在增大；而本发明提出的基于互耦校正的协方差矩阵重构方法在高信噪比条件下性能极为接近理论最优值，在低信噪比条件下算法的性能有所下降，这是因为在期望信号功率低于噪声水平时，doa估计会发生失准，从而影响波束形成器的性能。

图3(a)和图3(b)的横轴表示采样样本数，纵轴表示波束形成器的输出信干噪比；图3(a)表示在存在信号观测误差且输入信噪比为20db时的仿真结果，图3(b)表示在存在信号观测误差且输入信噪比为-5db时的仿真结果。仿真结果表明，在期望信号的输入信噪比比较高时，本发明所提出的波束形成方法性能大幅优越于其他波束形成方法；在低信噪比的情况下如果能够保证样本充足，本发明提出的波束形成算法仍然具有很好的性能。

图4的横轴表示输入信噪比，纵轴表示输出信干噪比；图4表示不存在信号观测误差，采样快拍数为30，几种波束形成方法的输出信干噪比随期望信号输入信干噪比变化的曲线。从图4中我们可以看到，在只考虑均匀圆阵的互耦造成期望信号和干扰信号导向矢量失配的条件下，经过本方法互耦校正后，波束形成器的性能在高信噪比情况下与理论最优值几乎没有差距，这是因为本方法只针对互耦因素进行校正，并且剔除了采样协方差矩阵中的期望信号分量，在不考虑其他失配因素的情况下可以达到接近理论最优的性能。

图5(a)和图5(b)的横轴表示采样样本数，纵轴表示波束形成器的输出信干噪比；图5(a)表示不存在信号观测误差且输入信噪比为20db时的仿真结果，图3(b)表示不存在信号观测误差且输入信噪比为-5db时的仿真结果。结果表明，在职考虑均匀圆阵的互耦造成期望信号和干扰信号导向矢量失配的条件下，本发明方法的性能相比考虑了信号观测误差是要好一些。

综上所述，仿真实验验证了本发明的正确性，有效性和可靠性。

以上所述，仅为本发明的具体实施方式，但本发明的保护范围并不局限于此，任何熟悉本技术领域的技术人员在本发明揭露的技术范围内，可轻易想到变化或替换，都应涵盖在本发明的保护范围之内。因此，本发明的保护范围应以所述权利要求的保护范围为准。