一种基于测力仪体弹性形变的标定方法与流程

本发明涉及一种基于测力仪体弹性形变的标定方法，应用于多点支撑压电传感器测力仪的标定。本方法避开了多传感器布置中存在的超静定问题，利用测力仪上板的弹性形变进行输出求解，之后进行加载标定，依据求解的理论值与实际输出值建立目标函数，优化求解，完成测力仪标定。

背景技术：

目前，国内外用于测力仪的静态标定方法主要为逐级加载标定法,步骤主要有加载以及求解。

标定的加载过程可以利用砝码、机械或液压的方式进行，这些方式具有简单、易于操作，还可以依据工况进行选择等优势。工况良好时，可以选用砝码加载，加载力值恒久稳定；加载力值大时，可利用机械加载配合加载环或标准力传感器进行；而对于不便于人员操作的工况，则可以选用液压加载等，易于控制。

对于求解过程，其方式一般有列写标定矩阵，坐标变换矩阵，还有利用干扰矩阵、最小二乘法以及多项式逼近，统计学等方法。其中，标定矩阵为常用求解方法，应用广泛，对于测量空间与理论空间不重合的情况，则通过坐标变换矩阵提升计算精度。最小二乘法是数据拟合的主要方法，可以起到减小误差、判断是否存在粗大误差的效果。干扰矩阵则是通过矩阵运算，减小标定力值对于结果的影响。对于利用多项式逼近，统计学或者神经网络运算等标定方法，由于其可以避开矩阵的求逆运算，故而避免了数值计算过程中病态的问题，进而提高了标定精度。

上述多种方法主要基于理论力学、材料力学的理论进行求解。求解时，由于不可避免地存在超静定问题，需要先进行假设，使得运算过程与实际加载产生偏差。对于求解时应用的优化方法，例如干扰矩阵，或是多项式逼近的方法，虽均可以起到减小误差、提高精度的效果。但是结果依旧存在局限性。此外，上述方式一般在测力仪坐标方向进行加载，偏斜加载时仍然不脱离坐标平面，在其他位置加载标定的情况较少。

技术实现要素：

本发明为了克服多点支撑传感器求解时出现的超静定问题，设计了一种基于基尔霍夫(kirchhoff)弹性板理论的求解方法，通过这种方法计算各个传感器在加载下的力分配规律。之后在对应加载点加载进行标定实验，依据各加载点输出，得出各传感器实际输出。最后结合理论与实际输出，建立目标函数，进行优化求解，完成标定。

本发明的技术方案：

一种基于测力仪体弹性形变的标定方法，该方法将多点支撑传感器测力仪标定时遇到的超静定问题转化为测力仪上板变形的求解问题。在给出测力仪中传感器布置位置的情况下，结合测力仪上板弹性变形的条件、载荷方程和边界条件，得到各传感器力的分配规律。之后进行标定加载实验，将测力仪安装、标定系统调试完毕后，在典型位置进行加载，记录并处理实验数据。数据处理过程运用kirchhoff理论得到的输出值与实际输出关系建立的目标函数，对目标函数的多次寻优处理，完成测力仪标定。

本发明方法由于需要结合理论输出与实际输出建立的目标函数进行灵敏度计算，故而首先要得到各传感器在加载状态下的理论输出值。故而第一步进行力分配的理论分析。

一种基于测力仪体弹性形变的标定方法，步骤如下：

第一步，将传感器的超静定问题转化为测力仪上板变形的问题，求解传感器的主向力

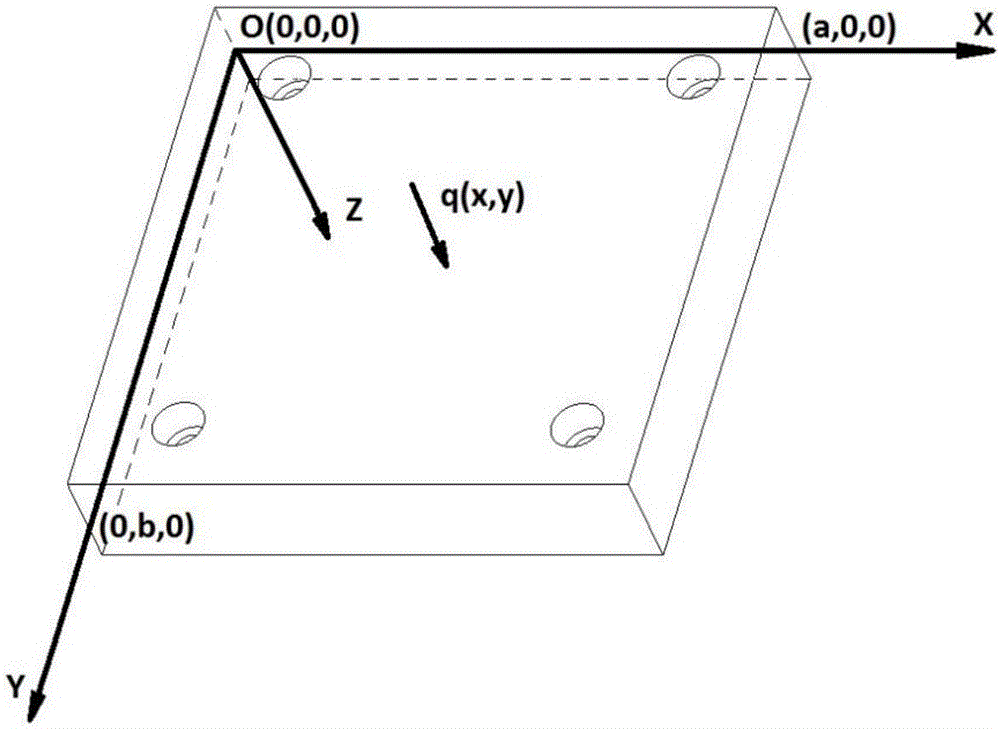
首先将kirchhoff理论应用于测力仪上板，建立坐标系：测力仪上板正面朝上，以一棱边的中点为坐标系原点o，以测力仪上板正面相互垂直的两个方向分别为x轴和y轴，以及该棱边所在直线为z轴，建立右手笛卡尔坐标系oxyz；得到其板弹性变形的弯曲方程为

式中，ω为测力仪上板法线方向上变形的挠度；q(x,y)加载应力；d为测力仪上板的抗弯刚度，由下式计算：

式中：δ、e和μ分别为测力仪上板的厚度、材料的弹性模量及泊松比；

再确立边界条件，包括固定边界和自由边界；其中，固定边界指传感器和测力仪上板接触边界，传感器本身刚度大，取接触边界的挠度为0，表达为：

式中：ai、bi为第i个压电传感器的横、纵坐标；

自由边界即不受约束的边界，即测力仪上板四周，不受约束；对于y＝b为自由边界的边，自由边界表示为：

联立上述方程，得到各传感器在点(i,j)的正应力σ(i,j)的公式为

对应传感器的主向力f(i,j)为：

由此得到具有n个传感器时各传感器的主向力值；

第二步，安装测力仪，进行标定

标定系统包括标定实验台、测力仪、压电传感器、电荷放大器、数据采集卡以及计算机；测力仪包括测力仪上板和测力仪下板，二者通过压电传感器连接，压电传感器主向力坐标系fz、侧向力坐标系fx、fy分别与总坐标系方向z、x、y对齐；压电传感器通过导线与电荷放大器连接；将测力仪安装到标定实验台，依次连接电荷放大器、数据采集卡和计算机，完成标定系统的安装；标定加载并记录数据；

第三步，进行数据处理，完成标定

依据标定得到的数据，结合kirchhoff理论，求解与实际加载后的输出值，建立两者的联系；即在加载力f作用下，将求解的理论输出力值fij，以及实际输出电压vij进行线性拟合，其中：下标i、j分别代表在第i个加载点，得到第j个传感器的输出，得到灵敏度sij；进一步拟合测力仪中各个传感器的灵敏度sj：

式中：n为加载点个数；利用各传感器灵敏度sj与输出电压求解vj，得到初始拟合合力fk，k＝0，并建立如下目标函数：

ek＝(f-fk)²，k＝0,1,2…n(8)

此时，以ek→min为目标，调节参数、多次优化计算(7～8)，得到最佳力值fopt；即得到测力仪在加载力值f的作用下的输出力值fopt，以及最佳灵敏度sopt，完成测力仪标定。

本发明的有益效果：基于kirchhoff理论，结合载荷方程、边界条件等方程，避开了多传感器布置下存在的超静定问题。同时通过目标函数的建立与寻优计算，提高了偏斜加载标定实验的实验精度。

附图说明

图1为本发明标定方法的流程图。

图2(a)为本发明涉及的测力仪上板建立的坐标系。

图2(b)为本发明涉及的测力仪体总装图。

图2(c)为本发明测力仪体去除上板后俯视图。

图3为本发明标定方法加载位置图。

图4(a)为输出最大偏差结果图。

图4(b)为输出平均偏差结果图。

图中：1测力仪下板；2压电传感器；3测力仪上板；4连接螺钉。

具体实施方式

以下结合附图和技术方案，进一步说明本发明的具体实施方式。

实施例

标定方法基于kirchhoff理论的进行解算，利用板变形的载荷方程、边界条件等方程，求解各个传感器的输出力值。之后在典型的加载点进行测力仪标定，得到各加载点输出，并以合力误差为目标函数，寻求最小值，进一步求得测力仪灵敏度。

实施例1，标定实验如图3所示。测力仪上板图2(a)尺寸为100×100mm，四个传感器安装于测力仪中心60×60mm正方形上。选用的加载点如图3所示，包括测力仪中心点(0,0)以及八个偏载力加载点d1(-35,0)，d2(0,35)，d3(35,0)，d4(0,-35)，e1(-30,-30)，e2(-30,30)，e3(30,30)，e4(30,-30)进行标定验证实验。

第一步进行标定系统的安装。

首先按照附图2装配测力仪体。测力仪体由测力仪上板3、测力仪下板1、压电传感器2，以及连接螺钉4组成。装配前，测力仪上板先按加载位置(图3)划线。装配时，传感器按照对角的顺序进行：先将2、4号位置旋入定位销，落入2、4号传感器，而1、3号传感器用连接螺钉连接至下板，使用直角尺依次调整传感器3、2以及传感器3、4的位置，保证定位精度后依次紧固1、3号传感器。并以1、3号传感器为基准，调整并紧固2、4号传感器。所有传感器紧固后，使用704胶使传感器侧面与测力仪下板凝固接触，并将12路输出导线旋入传感器，导线另一端接入电荷放大器。胶凝固之后，将连接螺钉旋出，小心落入上板，调整位置后，旋入并紧固连接螺钉，完成测力仪体装配。

测力仪装配好后，将测力仪体连接到标定实验台上，并连接其他器件。其中，电荷放大器型号为sinocerapiezotronicsln5861，对应四个放大灵敏度为3.42pc/n、3.42pc/n、3.67pc/n、3.57pc/n。选用加载环为02606，加载精度为0.1n，量程为0-6000n。

第二步进行加载标定实验。

依据图3加载位置，从中心(0,0)开始，依次在d1～d4，e1～e4点进行加载，采用阶梯加载，力值为从0n至5000n(间隔为1000n)。为了保证数据的真实性，每个加载位置进行三次重复加载实验，记录并整理实验数据。

第三步对采集的实验数据进行处理。

数据处理主要以d1～d4点为基础，结合误差优化函数，完成测力仪标定，用得到的结果和常规的标定方法进行比较，对比这两种方法在e1～e4点的合力误差大小。对比处理之后，得到多点加载与单点拟合的最大偏差与平均偏差的折线图，如图4(a)(b)所示。其中，多点拟合的总体平均偏差为17.87n，占量程的0.35％，相对于单点拟合结果26.45n(量程的0.53％)相对较好；对于最大偏差，多点拟合的结果为72.16n(量程的1.44％)，而单点拟合的结果为78.5n(量程的1.5％)，也相对较优。

综上所述，本发明采用kirchhoff理论，并结合目标函数等求解方法进行标定实验。从结果来看，平均偏差以及最大偏差的拟合结果均有提升。这种标定方法避开了多点支撑传感器测力仪中存在的超静定问题，提升了标定精度，更符合高精度测试的要求。