一种两轴姿态倾角测量方法与流程

本发明属于惯性导航技术领域，特别涉及一种两轴姿态倾角测量方法。

背景技术：

惯性导航技术是20世纪中期发展起来的完全自主式导航技术。通过惯性测量组件测量载体相对惯性空间的角速率与加速度信息，利用牛顿运动定律自动推算载体瞬时速度与位置信息，具有不依赖外界信息、不向外界辐射能量、不受干扰、隐蔽性好的特点。能连续地提供载体的全部导航、制导参数(位置、线速度、角速度、姿态角)，广泛运用于航天、航空、航海领域，特别是军事领域。而两轴姿态倾角的准确估量是实现运动物体控制的关键参数。

譬如对农业机械而言，导航作业时，由于田面的不平整，单纯依赖gnss定位并不能保证拖拉机直线作业，只有借助车身实时横滚角与俯仰角信息进行投影校正，方能保证拖拉机按照规划路径准确行走作业。又如平地机与喷雾机作业时，作业质量的保证取决于平地铲与喷杠的水平，这要求农机具姿态检测信息的实时反馈，以保证水平作业。同时准确的姿态倾角检测更是农业机械与农机具动力学建模、作业安全预警的研究的基础。

目前姿态倾角检测多采用惯性传感器、图像处理等方法获取，还有一些采用多种传感器融合技术进行姿态监测。其中惯性传感器一般采用加速度计和陀螺仪、倾角传感器、超声波传感器等对姿态进行监测。传感器融合技术主要是将多个传感器结合起来对姿态倾角进行监测。利用mems传感器实对姿态倾角测量是目前应用最广泛的方法，其经济性、稳定性和适应性指标相比其他测量方法都具有突出优势。

目前广泛应用于军工、航天航空、船舶、汽车、机器人等各个领域的高精度姿态传感器价格昂贵，适用性有限。低成本的姿态倾角传感器一般采用简单的互补滤波等简单算法进行融合，测量精度有限。且大多缺乏考虑姿态倾角零偏问题，产生许多实际应用问题。

姿态倾角更新解算是惯性导航系统的关键算法，传统的姿态倾角更新算法有欧拉角法、方向余弦和四元素法。四元素法计算时需要进行泰勒展开，通常采用忽略其高阶项将非线性转化成线性进行姿态估算，存在误差。方向余弦总共有9个参数，计算量大，不适宜工程应用。欧拉角法是直接迭代欧拉角微分方程，计算最为简便直接。陀螺仪存在固有零偏，长时间积分运算存在累积误差，不适合单独使用。加速度计可以解算准静态峡物体欧拉姿态角，无积分运算不存在累积误差问题，但其解算的姿态角动态响应差，无法在动态条件下应用。目前国内外已经开发多种将两类器件相结合的融合算法，例如互补滤波、卡尔曼滤波、梯度算法、模糊算法等，其中数卡尔曼滤波算法应用最为广泛。

技术实现要素：

本发明的主要目的在于克服两轴姿态倾角测量的需求以及惯性传感器测量技术存在的问题，提供一种两轴姿态倾角测量方法，通过传感器模型与算法模型的构建，提供一种两轴姿态倾角精准测量方法，并考虑其应用的实际问题。

为了达到上述目的，本发明采用以下技术方案：

本发明一种两轴姿态倾角测量方法，包括下述步骤：

s1、基于三轴加速度计空间几何模型模型，准静态情况下对横滚角与俯仰角初始值进行准确估算，并作为卡尔曼滤波器的状态输入量；

s2、将两轴倾角零偏biasroll、biaspitch也作为卡尔曼滤波的状态输入量；

s3、将x轴陀螺仪与y轴陀螺仪测量值gyrox、gyroy作为卡尔曼滤波的输入向量；

s4、建立包含4个状态向量与2个观测向量的系统卡尔曼滤波状态方程和测量方程，精准测量两轴姿态倾角。

作为优选的技术方案，步骤s1之前，还包括硬件平台的搭建步骤，所述硬件平台具有稳定可靠3轴加速度计、2轴陀螺仪与温度信息输出装置，输出频率不小于10hz。

作为优选的技术方案，在传感器预热准静态过程根据三轴加速度计空间模型完成状态向量初始值估算。

作为优选的技术方案，在步骤s1中，三轴加速度计空间几何模型模型的构建如下：

首先，建立姿态倾角测量系统坐标系，绕坐标系x轴转动为横滚角，绕坐标系y轴转动为俯仰角，基于欧拉角的物理特性，在平台式惯性导航系统中，欧拉角可通过坐标系的3个框架的角传感器测量；

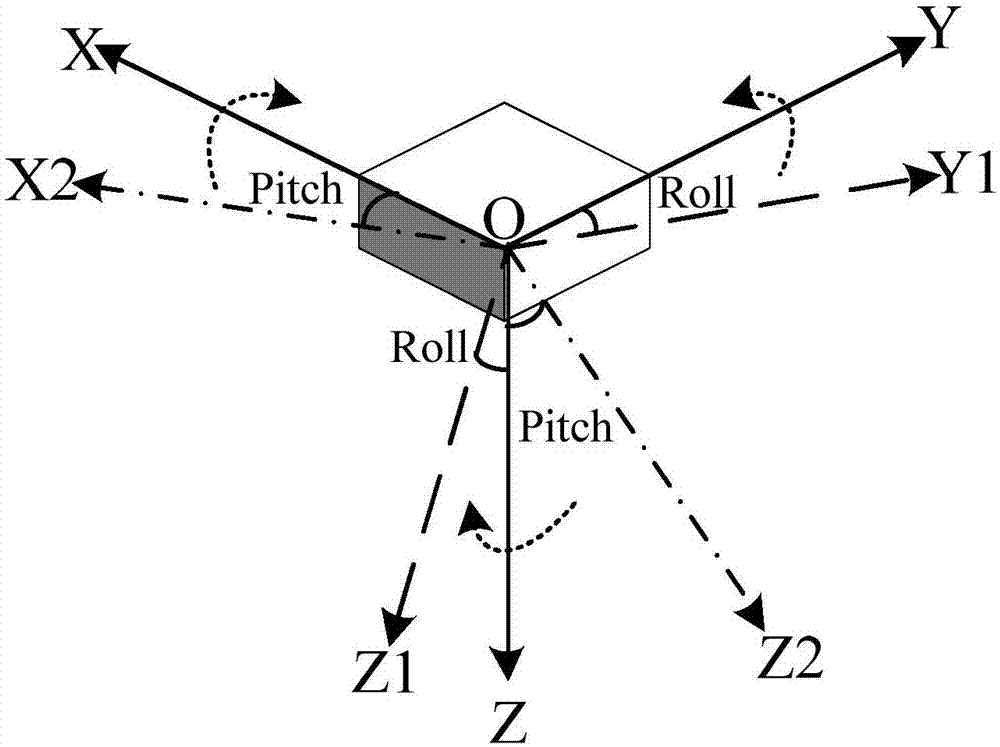
其次，设姿态测量系统原始坐标系为o-xyz，当绕x轴转动时产生横滚倾角roll，传感器坐标系变为o-xy1z1；当绕y轴转动时产生俯仰倾角pitch，传感器坐标系变为o-x2yz2；

根据欧拉角法的坐标旋转原理，欧拉角随时间的传递关系可利用惯性传感

器测得的角速率表示：

式中：ωx、ωy、ωz分别为x、y、z轴的角速率，φ、θ、ψ分别为横滚角向量、俯仰角向量与偏航角向量，整理推导出欧拉角的微分方程为：

最后，根据欧拉角法，只需求解相应的微分方程便可得到相应的姿态角。

作为优选的技术方案，在步骤s1中，初始传感器为准静态，利用三轴加速度计的空间几何模型估算姿态原始量：

横滚角初始值

俯仰角初始值

其中accx、accy、accz分别为三轴加速度计的测量值，由此可估算2个初始状态向量。

作为优选的技术方案，在步骤s2中，两轴倾角零偏biasroll、biaspitch初始值为0。

作为优选的技术方案，步骤s4具体为：

建立姿态参考系统的外部拓展卡尔曼滤波状态方程与测量方程：

其中xk和zk分别表示姿态参考系统的状态向量与观测向量，uk-1为系统输入，ωk-1和υk分别为状态方程的过程误差与测量方程的测量噪声，k表示本次计算的时序，a，b，h分别是系统状态矩阵、系统输入矩阵、输出矩阵，其中：

系统的状态向量为

系统状态矩阵为

系统输入矩阵为

系统观测向量为zk＝[rollk,pitchk]^t；

系统输出矩阵k表示本次计算的时序，δt表示融合时间。

作为优选的技术方案，状态方程的过程误差ωk-1与观测方程的测量误差υk均假设为零均值且符合正态分布的高斯白噪声，对应着系统的过程误差协方差矩阵qk和测量误差协方差矩阵rk，其中：

ωk～n(0,qk)，υk～n(0,rk)且cov[ωk,υk]＝0；

其中k表示本次计算的时序，δt表示融合时间。

本发明与现有技术相比，具有如下优点和有益效果：

1、本发明采用3轴加速度计与2轴陀螺仪惯性传感器，集成度高，性能稳定，成本低。

2、本发明方法考虑两轴倾角零偏，利用卡尔曼滤波融合方法自动修正，保证两轴倾角的高精度测量。

3、本发明搭建系统的具有4个状态向量和2个观测向量的外部拓展卡尔曼滤波模型进行姿态角融合，保证两轴姿态测量精度。

附图说明

图1为本发明一种两轴倾角测量系统示意图；

图2为欧拉角姿态解算的示意图；

图3为三轴加速度计空间模型示意图；

图4本发明横滚倾角与mti-300比较示意图；

图5本发明俯仰倾角与mti-300比较示意图。

具体实施方式

下面结合实施例及附图对本发明作进一步详细的描述，但本发明的实施方式不限于此。

实施例

如图1所示，本实施例一种两轴姿态倾角测量方法：包括对2轴陀螺仪与3轴加速度计的卡尔曼滤波姿态融合算法。准静态情况下进行估算，利用三轴加速度计的三维空间几何模型估计姿态横滚角、俯仰角的初始值，并作为卡尔曼滤波器的状态输入。建立包含4个状态向量与2个观测向量的系统卡尔曼滤波状态方程和测量方程。本发明方法考虑两轴倾角零偏，可避免姿态倾角估算时引入偏差；而建立卡尔曼滤波系统方程可以保证在两轴倾角精度。

首先是硬件平台的搭建，本发明的硬件平台具有稳定可靠3轴加速度计、2轴陀螺仪，输出频率不小于10hz。由于本发明重点在于姿态倾角融合算法介绍，故详细的硬件平台信息不在此展开介绍。

建立姿态倾角测量系统坐标系，绕坐标系x轴转动为横滚角，绕坐标系y轴转动为俯仰角。基于欧拉角的物理特性，在平台式惯性导航系统中，欧拉角可以通过坐标系的3个框架的角传感器测量。如图1所示，姿态测量系统原始坐标系为o-xyz，当绕x轴转动时产生横滚倾角roll，传感器坐标系变为o-xy1z1；当绕y轴转动时产生俯仰倾角pitch，传感器坐标系变为o-x2yz2。根据欧拉角法的坐标旋转原理，欧拉角随时间的传递关系可利用惯性传感器测得的角速率表示：

式中：ωx、ωy、ωz分别为x、y、z轴的角速率，φ、θ、ψ分别为横滚角向量、俯仰角向量与偏航角向量。整理可推导出欧拉角的微分方程为：

故根据欧拉角法，只需求解相应的微分方程便可得到相应的姿态角。

如图3所示：准静态情况下，利用三轴加速度计的空间几何模型估算姿态倾角原始量：其中横滚角初始值俯仰角初始值

其中accx、accy、accz分别为三轴加速度计的测量值，由此可估算2个初始状态向量。

建立姿态倾角参考系统的外部拓展卡尔曼滤波状态方程与测量方程：其中xk和zk分别表示姿态倾角参考系统的状态向量与观测向量，uk-1为系统输入，ωk-1和υk分别为状态方程的过程误差与测量方程的测量噪声，k表示本次计算的时序，a、b、h分别为系统状态矩阵、输入矩阵与输出矩阵，其中：

系统的状态向量为

系统状态矩阵为

系统输入矩阵为

系统观测向量为zk＝[rollk,pitchk]^t；

系统输出矩阵

作为优选的技术方案，状态方程的过程误差ωk-1与观测方程的测量误差υk均假设为零均值且符合正态分布的高斯白噪声，对应着系统的过程误差协方差矩阵qk和测量误差协方差矩阵rk，其中：

ωk～n(0,qk)，υk～n(0,rk)且cov[ωk,υk]＝0。

如图4、图5所示，为本发明两轴倾角与mti-300测量结果比较，由图可知该方法测量精度与mti-300相当，动态测量精度可达0.7°，性能稳定。

上述实施例为本发明较佳的实施方式，但本发明的实施方式并不受上述实施例的限制，其他的任何未背离本发明的精神实质与原理下所作的改变、修饰、替代、组合、简化，均应为等效的置换方式，都包含在本发明的保护范围之内。