一种利用粒子滤波的雷达微弱目标检测跟踪方法与流程

技术领域个

本发明属于通信电子技术领域，涉及一种利用粒子滤波的雷达微弱目标检测跟踪方法。

背景技术：

为了应对隐身目标等非合作目标给现代雷达带来的挑战，无源定位与跟踪方法正在蓬勃发展，无源体制信号探测技术中一个关键问题就是对微弱机动目标进行检测与跟踪。微弱目标指的是雷达反射截面积很小，导致反射回波很弱的低可探测性目标。这些目标被电磁波照射时，后向散射波强度明显下降，回波信号非常微弱。同时，这些典型的微弱目标又往往具有非常高的机动性，即这些目标能够改变自身原有的运动规律，导致运动模型变化的程度超过了滤波器模型所能跟踪匹配的范围，即造成模型失配。传统雷达对这些目标的探测距离大为缩短，探测的灵敏度也大为降低。所以，传统的门限检测和跟踪方法对于微弱机动目标不具优势，技术革新迫在眉睫。

现有的检测跟踪算法的主要缺点是跟踪非线性运动的目标时容易形成模型失配，而且计算代价很大。因此，设计检测跟踪算法时需要考虑的两个主要因素是能耗和跟踪精度。考虑到能耗限制以及精度需求，传统的粒子滤波算法包括以下步骤：

(1)采样随机生成一组粒子。

(2)更新重要性权重。

(3)计算归一化的重要性权重。

(4)计算估计有效粒子数量。

(5)判断有效粒子数量是否超过阈值。

(6)如果步骤5为假，则进行重采样。

(7)当生成粒子组数超过额定数值时，根据粒子的估计量计算待估参量，输出状态估计。上述传统方法存在以下不足：

(1)计算代价巨大，容易造成数据处理单元溢出。

(2)采样过程判断单一，引起粒子退化，损失估计精度。同时，为了解决重采样之后粒子退化的问题还需要增大粒子数量，进一步增加了计算耗费。

(3)容易产生测量数据跳变点，造成角度模糊和模型失配。

技术实现要素：

本发明所要解决的，就是针对上述问题，提供一种减少计算消耗的改进的序贯平滑的粒子滤波(improvedsequentialsmoothing-particlefilter,iss-pf)算法，该方法可以有效跟踪线性运动的目标，并且对于非线性运动的微弱机动目标也有很好的检测跟踪效果。算法首先减少传统粒子滤波的粒子数量，从被跟踪目标可能的分布中采样得到少量的采样点。计算得到这些点的平均值和协方差，对两者进行加权。选择合适的参数，并且把这些点传递给非线性变换函数来模拟机动目标的运动。确保采样点的对称性，从变换后的点产生另一过程。对变换后的点进一步平滑处理，再判断是否序贯进行粒子滤波和重采样。通过上述步骤实现改进的序贯平滑的粒子滤波器。

本发明的技术方案主要步骤可以概括为：

(1)计算建议分布的均值协方差

(2)生成采样点

(3)对每个采样点赋予权重

(4)选择合适的参数使得采样点有合理的分布

(5)对采样点做非线性变换

(6)对变换后的点做平滑处理

(7)计算平滑以后的均值和方差，重新估计建议分布，

(8)若有效粒子数量不足，从平滑后的分布函数中重采样，重新进行序贯的粒子滤波

(9)输出带平滑的滤波结果。

本发明的有益效果为，本发明的方法通过对每一个采样点引入不同的权重，对变换后的采样点进行平滑处理，实时修正了滤波误差，确保实现了最终输出得到目标位置的估计。仿真结果表明本算法的定位精度高于现有的粒子滤波算法，并且计算开销较低。

附图说明

图1为本发明的流程示意图；

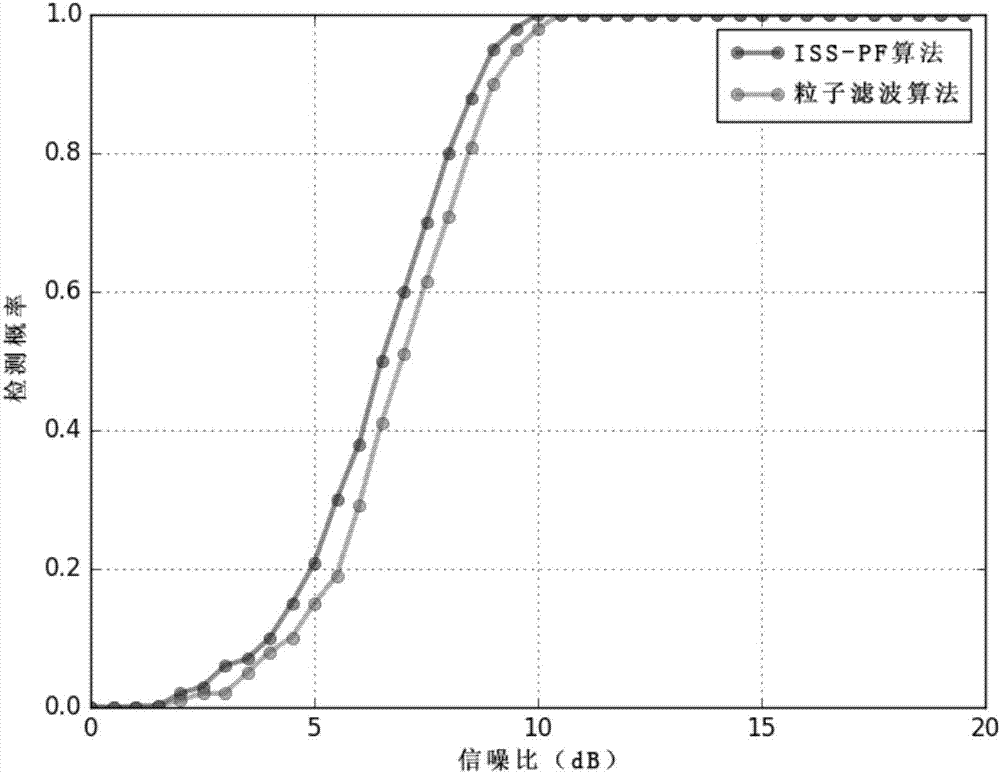
图2为本发明的方法和和传统的粒子滤波算法的检测概率曲线图。

具体实施方式

在20×20的正方形区域内分布做非线性运动的目标，序贯时间长度为30帧，设置目标速度的最大变化量为1m/s，目标的最大速度为680m/s，目标的初始状态向量为[6，7，0.2，0.4]。蒙特卡洛仿真次数为100。噪声功率为σ²＝1/2，信噪比为信号幅度均值的平方和噪声功率比值的对数，信噪比变化从0db-15db。

(1)首先计算建议分布的均值和协方差，并以此作为采样点分布的依据。

cov(x，y)＝e[(x-μx)(y-μy)](2)

其中p(x)表示随机变量在x处出现的概率大小，μ表示变换前建议分布的均值，μx为变量x的均值，μy为变量y的均值，cov(x，y)表示两个变量的协方差。

(2)选择建议分布的均值作为第一个采样点，在第一个采样点的两侧分别对称地选取两组采样点，使得采样点的分布符合下列约束方程：

其中w^m和w^c分别表示步骤一中均值和方差的权重，f(x)表示非线性函数，ξi表示了第i个采样点，f(ξi)表示非线性函数在ξi处的取值。n表示输入向量x的维度。

(3)为了方便表示，引入可变参数α，β，κ，定义参数λ为

λ＝α²(n+κ)-n(7)

对所有步骤(2)中采样点的均值和方差赋予不同的权重，使得所有采样点的权重和为一，并且符合计算式：

其中，下标i表示选择的是矩阵的第i列向量，σ表示协方差矩阵。这个过程等效为：用一个常数来缩放协方差矩阵，取矩阵的平方根，并通过同时从均值中加上和减去这个平方根来确保采样点及其权重的对称性。

(4)计算ξ0的均值的权重为

(5)ξ0的协方差的权重是

(6)其余部分点的平均值和协方差的权重相同，如下式所描述：

(7)选择合适的参数α，β，κ，使得采样点位于第一和第二标准差椭圆的内部，或者位于第一第二标准差椭圆之间。

第一标准差σ和第二标准差2σ中，参数σ的计算如下：

其中xi表示随机变量在第i个采样点处的取值。

(8)将采样点通过非线性变化。

(9)对变换后的点集做平滑处理：

(a)开始，选择一个状态点，使得其他有一部分采样点落在以该点为中心，半径为r的区域内，这些采样点的分布符合滤波器对后验概率的估计：

其中表示狄拉克函数在采样点处的取值，y0：k-1表示序列y0，y1，...，yk-1，表示对后验概率密度函数p(dxk|y0：k-1)的估计。

(b)根据以下公式对采样点前后时刻的估计位置做加权平均

其中k(x0，xi)表示平滑运算的加权值，表示当前平滑点的估计值，ri表示第i个平滑窗的半径，只有进入区间的采样点才参与平滑计算。

(10)计算平滑后采样点的均值和方差，根据平滑以后的均值和方差重新估计建议分布，并从平滑后的分布函数中重采样。

(11)重复上述步骤直到序贯滤波次数足够，并输出滤波结果。

本算法在信噪比为0db-15db的情况下，总共进行100次蒙特卡洛仿真进行检测，确保得到了较高的检测概率和检测精度，从下表1可以得出，而改进算法的检测概率在7db时优于现有的粒子滤波算法，计算代价也小于现有的粒子滤波算法。

表1本发明的方法和和传统粒子滤波算法计算耗时对比