一种基于高分辨距离像IMF特征的雷达目标识别方法与流程

本发明应用于高分辨距离像(high-resolutionrangeprofile，hrrp)处理、雷达目标识别、非平稳信号时频分析领域，具体涉及hrrp的特征模态函数特征提取和雷达目标识别方法。

背景技术：

对信号最直观的表示是时间描述，即时域表达。经典的分析与处理平稳信号的最常用、最主要的方法是傅里叶变换，通过该变换可以得到信号的频域表示。傅里叶变换是一种全局变换，频谱能够体现信号中的频率成分，并且可以观测到频率成分的能量大小和相位信息，但不能解释频率成分发生在什么时刻以及持续时间，对于发生在信号开始时或发生在信号中一段时间内的频率值相同的频率无法区分。由于时频分析由于增加了频域特征量，相对于单纯的时域或频域分析而言非平稳信号的时频表示更能反映它的时变特性。信号的时频表示其实就是使用时间和频率的联合函数来表示该信号。对非平稳信号进行时频分析时，往往需要先分析其瞬时频率的变化情况。但是对某些非平稳信号直接进行瞬时频率分析时往往出现分析的结果和实际情况不符的现象。l.cohen研究发现，对于单分量信号进行瞬时频率分析时得到的结果与实际情况一致，而对多分量的非平稳信号进行时频分析时，由于其特性不满足瞬时频率的定义，所以分析的结果与实际情况不符。而且他还发现其非平稳特性本质上是由单分量相互作用决定的。l.cohen提出了单分量信号和多分量信号概念，其中多分量信号数学模型为：

式中n(t)为多分量信号中的噪声成分，xi(t)为该多分量信号内的单分量信号，n为该多分量信号中所包含的单分量信号个数。即多分量信号由多个单分量信号和噪声信号共同组成。其中单分量信号在每一时刻内只有一个频率，即每时刻仅存在一种振动模态，对此类信号计算的瞬时频率才有实际意义。计算多分量信号瞬时频率时应该将其分解为多个单分量信号后，再对各个单分量信号求瞬时频率，所有单分量信号瞬时频率的共同组合表示该多分量信号瞬时频率。

在2014年konstantindragomiretskiy和mominiquezosso提出变分模态分解(variationalmodedecomposition，vmd)算法，当变分模态分解算法的参数设置合理的话则可以很好的分解出多分量非平稳信号的单分量特征模态函数(intrinsicmodefunction,imf)以及与之对应的中心频率。各个单分量imf的瞬时频率能很好地反映多分量非平稳信号的实际变化情况。高分辨距离像(hrrp)是为获得目标的有效信息,由高分辨率宽带雷达发射一定频率信号并接收经过目标反射后的回波信号,是典型的多分量的非平稳信号，其中必然含有目标的固有特征信息。而目标的类型和几何形状决定了回波信号的瞬时相位和瞬时频率的变化,从而提供了鉴别各类目标的基础,因此可以利用hrrp进行目标分类识别。

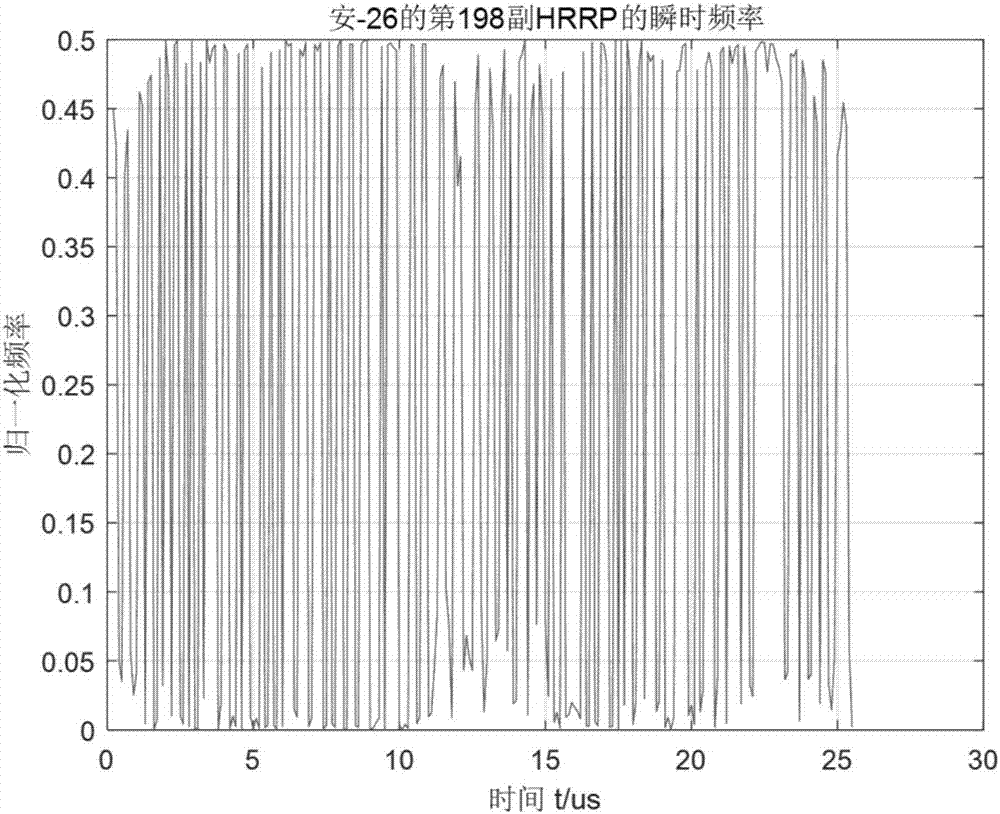
在众多基于时频分析方法提取hrrp时频特征的算法之中，基于hrrp的瞬时频率特征进行雷达目标识别是一种很常用的方法，但是该方法忽略hrrp为多分量非平稳信号的特性，直接对多分量hrrp进行瞬时频率特性进行分析，得到的结果并不能反映出hrrp实际的时频特性。势必丢失了很多有利于雷达目标识别的信息甚至得到错误信息。图2画出了安-26第198幅hrrp的瞬时频率随时间变化情况，通过该图并不能了解到该hrrp的瞬时频率实际变化特点。因而很有必要对hrrp进行单分量分解即得到其imf,不同目标的hrrp分解得到的imf中心频率往往存在差异，所以可以应用imf的中心频作为特征量进行雷达目标分类识别。鉴于此，本发明提出了基于高分辨距离像imf特征的雷达目标识别方法。通过该方法可以得到较高的雷达目标正确识别率。

技术实现要素：

本法明针对目前众多应用基于时频分析方法直接获取多分量非平稳hrrp信号的时频特征，而忽略研究其所包含的单分量瞬时频率分布情况，导致很多有利于雷达目标识别的信息的丢失甚至得到错误信息，进而造成雷达识别率不高的问题。本发明公开了一种基于高分辨距离像imf特征的雷达目标识别方法。

本发明技术方案为:一种基于高分辨距离像imf(特征模态函数)特征的雷达目标识别方法，其特征在于，该方法包括以下步骤：

步骤1:通过高分辨率宽带雷达获取雷达目标的高分辨距离像(hrrp)；每个目标的高分辨距离像均是由一个m行，n列的矩阵构成；矩阵的每一行代表一幅距离像，而每一列代表其所在行的一个距离单元；目标个数大于等于2个；

步骤2:采用变分模态分解算法把每一幅距离像分解为多个单分量imf,同时得到每个imf的中心频率；最终，每个目标高分辨距离像数据的所有单分量imf对应的中心频率组成一个m行k列的矩阵，称该矩阵为中心频率矩阵，其中k表示一幅距离像分解出的单分量imf的个数；

步骤3:在步骤2得到的中心频率矩阵中，保持各中心频率的行位置不变，调整其所在列的位置，调整方法为：计算中心频率矩阵每一列的均值，针对每一列，寻找出该列中与均值相差最大的r个中心频率，这r个频率称之为待调整中心频率，r的大小根据实际情况确定；分别计算出这r个待调整中心频率与其它列均值的距离；然后，找出每一个待调整中心频率距离最近的列均值；并用这r个待调整中心频率分别取代与距离最近的列均值所在列对应位置的中心频率,将被取代的r个中心频率分别额外保存为r个中间变量；再采用上述调整方法把这r个中间变量调整到与其距离最近的列均值所在列的对应位置，再将此时被取代的r个中心频率额外保存为r个中间变量；按照上述方法依次循环进行下去，直至第n+1次待调整的r个中间变量，与第n次待调整的r个中间变量完全相同，则停止调整；其中n为正整数。

步骤4:计算出各目标的识别特征量，计算方法为：将步骤3获得当前目标中心频率矩阵的每一列与其余各目标对应列进行比较，获得一个差异度；选取出差异度最大的i列中心频率，作为当前目标的识别特征量；

步骤5：采用步骤4获得的识别特征量，通过k近邻分类器识别出该目标的类型。

进一步的，所述步骤4的具体方法为：采用k-w检验特征选择方法和fisher判决率的加权特征选择方法，分别计算出当前目标中心频率矩阵的每一列与其余各目标对应列的差异度；分别对两种方法计算出的差异度进行排序；确定识别特征量的列数i，i的大小根据实际情况确定，判断两种排序结果中最大的i个差异度包括的列是否相同，若相同则选取这i个列作为识别特征量；若不同则判断最大的i+1个差异度包括的列中是否存在i个相同的列，若存在，则选取这i个列作为识别特征量，若不存在则继续判断最大的i+2个差异度包括的列中是否存在i个相同的列；直到寻找出i个相同列作为识别特征量。通过综合考虑两种特征选择算法各自计算出的最优特征量来确定最终作为目标识别的特征量，这样提高了目标识别特征量的稳健性，降低了姿态敏感性的影响，进而提高了识别率。而且该方法快速高效，确保了目标识别的实时性。实施例图5,反映了应用该方法确定的三个特征量imf-w-2、imf-w-4和imf-w-6确实能很好地把实施例中三种目标区分开。

进一步的，所述步骤4中i的大小为3或4。当i值太小时选取的特征量较少，不利于区分开多个目标，当i值太大时选取的特征量冗余，降低了识别效率。i值取为3或4既保障了良好的区分出各个目标，又确保了识别的高效性。

进一步的，额外的还包括步骤6,该步骤采用步骤4中各目标识别特征量的前三分之一数据作为步骤5中k近邻分类器的样本数据,采用步骤4中各目标识别特征量的后三分之二数据作为步骤5中k近邻分类器的测试数据,采用该k近邻分类器判断各测试数据属于哪一个样本数据代表的目标,从而判断步骤4获得的识别特征量的稳定性。这样能够测试特征量稳健性能的高低，以及观测识别效果受姿态敏感性影响的程度；为评价选取的特征量优良程度提供充分的数据资源。

实施例，图6给出了应用本法明提出的方法对雷达目标进行分类的结果。安-26若能正确分类，形状标记为“*”，否则错误分到yak-42,形状标记为“o”,错误分到奖状，形状标记为“六角星形”；yak-42若能正确分类，形状标记为“·”,否则错误分到an-26,形状标记为“五角星形”,错误分到奖状，形状标记为“^”；奖状若能正确分类，形状标记为“+”，否则错误分到an-26,形状标记为“正方形”,错误分到yak-42，形状标记为“菱形”。从图6可以看出绝大多数目标被正确分类。统计结果显示，该实施例的识别率到达95.74％，明显好于通常仅仅基于时域或频域的特征量进行目标识别的效果。

附图说明

图1本发明实施步骤流程图；

图2安-26第198幅hrrp的瞬时频率；

图3安-26第198幅hrrp的第十个imf的频域；

图4安-26第198幅hrrp的第十个imf的瞬时频率；

图5以imf-w-2、imf-w-4和imf-w-6三列中心频率为坐标画出三种飞机中心频率分布的

三维图。

图6雷达目标的分类结果

具体实施方式

以下将配合实施例来详细说明本发明的实施方式，以便对如何应用本发明技术手段来解决技术问题有更加深刻的理解，以期达到良好地解决实际问题目的，并据以实施。本发明基于高分辨距离像特征模态函数特征的雷达目标识别方法，本发明实施步骤流程如图1所示，各步骤具体按照以下方式实施：

步骤1:获取不同雷达目标的hrrp(高分辨距离像)数据；

本发明用到的hrrp数据是由国内某研究所使用高分辨宽带雷达外场实测数据，包括“雅克-42”中型喷气飞机、“奖状”小型喷气机、“安-26”小型螺旋桨飞机等共三种目标的hrrp数据。每个目标的hrrp数据是一个780行256列的矩阵。其中，行数780代表有780幅距离像，列数256代表每幅距离像有256个距离单元。

步骤2:应用粒子群优化算法选取变分模态分解算法的最优参数：

使用粒子群优化算法确定变分模态分解将hrrp分解成imf的个数k和二次惩罚参数α。

步骤3:使用步骤2获得的结果作为变分模态分解的参数，并对相应的hrrp进行imf分解,同时得到每个imf的中心频率。最终，每个目标hrrp数据的所有单分量imf对应的中心频率组成一个780行16列的矩阵，称该矩阵为中心频率矩阵。

步骤4:计算中心频率矩阵每一列的均值，并把每一列中偏离该列均值较大的中心频率调整到与该频率最接近的列均值所在的列，并保持所在行不变：

计算每个目标的相同模态级数的中心频率的均值，记为imf_n_mean。原则上相同目标的不同幅距离像的特征模态函数的分布相同，即特征模态函数分量个数以及相同模态级数的中心频率都相同。但由于杂波和噪声的干扰，往往会导致个别距离像的某些模态级数的频率值与其他大多数相同模态级数的频率值不一样，而是被分解到相邻级数模态上。通过计算每个中心频率与各个模态的均值imf_n_mean差值的绝对值sub_n_abs,当sub_n_abs取到最小值时，便将该频率值移到该均值对应的模态级数上，完成中心频率的排序调整。图3画出了安-26第198幅hrrp的第十个imf的频域。图4给出了安-26第198幅hrrp的第十个imf的瞬时频率。从图3得知该imf的归一化频率为0.1953。由图4可知该imf的瞬时频率大多数时间在0.1953上下波动，这是由于噪声干扰造成的。结合图3和图4即imf的频域和瞬时频率可知imf为含有噪声的平稳单分量。

步骤5:通过基于k-w检验特征选择和基于fisher判决率的加权特征选择这两种算法选取三列不同中心频率矩阵列相同且区别较大的中心频率作为目标识别的特征量：

通过基于k-w检验特征选择算法得到的前三个最大dif_value的值分别为1556、1536和1535，依次对应为imf-w-2、imf-w-6和imf-w-4。其中，imf-w-2代表中心频率矩阵的第二列，其他含义一样。通过基于fisher判决率的加权特征选择算法得到的前三个最大dif_value的值分别为4.063、3.682、和2.342，依次对应imf-w-4、imf-w-2和imf-w-6。其中，imf-w-2代表中心频率矩阵的第二列，其他含义一样。图5给出了应用这两种算法求得的特征量imf-w-2、imf-w-4和imf-w-6为坐标，画出三种飞机目标中心频率分布结果。该图表明选取的三个特征量确实区分度比较大。

步骤6:应用选取好的特征量对雷达目标进行分类。

应用步骤5中选取好的特征量作为不同目标分类的依据。使用k邻近(knn)分类器进行分类。选取三分之一的样本来用来学习，计算同一目标的中心频率的均值，其余的三分之二样本用来测试。实施例，图6给出了应用本法明提出的方法对雷达目标进行分类的结果。安-26若能正确分类，形状标记为“*”，否则错误分到yak-42,形状标记为“o”,错误分到奖状，形状标记为“六角星形”；yak-42若能正确分类，形状标记为“·”,否则错误分到an-26,形状标记为“五角星形”,错误分到奖状，形状标记为“^”；奖状若能正确分类，形状标记为“+”，否则错误分到an-26,形状标记为“正方形”,错误分到yak-42，形状标记为“菱形”。从图6可以看出绝大多数目标被正确分类。统计结果显示，该实施例的识别率到达95.74％，明显好于通常仅仅基于时域或频域的特征量进行目标识别的效果。

上述说明示出并描述了发明应用的实施例，但如前所述，应当理解本发明并非局限于本文所披露的形式，不应看作是对其他实施例的排除，而可用于各种其他组合、修改和环境，并能够在本文所述发明构想范围内，通过上述教导或相关领域的技术或知识进行改动。而本领域人员所进行的改动和变化不脱离发明的精神和范围，则都应在发明所附权利要求的保护范围内。