一种基于光子计数激光雷达的最优编码生成及解码方法与流程

本发明属于激光雷达技术领域，特别是涉及到极弱光探测领域，具体地说是一种基于光子计数激光雷达的最优编码生成及解码方法。

背景技术：

光子计数激光雷达是极弱光探测的有效手段，能够响应回波信号中的每一个光子，有效解决激光雷达有限的系统资源和整体性能之间的矛盾；具有极高的灵敏度和皮秒级的时间分辨率，可以实现高速大容量、高精度、低功耗的距离和空间的三维信息获取。

然而由于光子计数技术一方面为了快速获取目标信息，另一方面为了获得合理的脉冲能量，故往往采用高重频激光器；但高重频激光器在满足单值测距的条件下有效测距范围很短，最大测距范围与激光器重复频率成反比；而不满足单值测距条件则无法分辨回波光子与发射脉冲的对应关系，即导致距离模糊问题。所以光子计数激光雷达不得不解决高重频导致的距离模糊问题。

通过伪随机编码对出射激光调制是一种有效的解决距离模糊问题的方法，伪随机编码的码长与系统最大有效探测距离呈线性正相关，故仅通过增大伪随机编码的码长的方法即可极大的扩大光子计数激光雷达的探测距离。此外，伪随机编码一般通过伪随机模式发生器高速产生，往往可达ghz级，故在提高探测距离的同时还提高了时间精度进而提高了测距精度。张宇飞、贺岩等人在2016年发表的论文《three-dimensionalimaginglidarsystembasedonhighspeedpseudorandommodulationandphotoncounting》中详细阐述了用m序列对光子计数激光雷达调制从而获得目标三维信息的过程，该文采用连续激光器与调制器组合的方案，当采用调制器对连续激光器调制时，不存在储能时间，但单脉冲能量低，时间精度不高，而且调制器价格不菲，增加了系统成本；当采用脉冲激光器时，能够克服以上问题，但受到脉冲激光器最大脉冲重复频率限制。

传统的伪随机编码，如m序列，具有易于获取，速度较快等优点；但往往只是二相编码，而不包含强度信息，故信号内部相关性不够强，且容易受到噪声干扰，进而影响测距精度；而且传统伪随机编码方法往往只能生成固定长度的编码序列而不能根据需求灵活调整，例如m序列只能产生长度为2ⁿ-1的伪随机编码序列。而且生成的编码往往是固定的序列，不能根据实际应用环境的要求进行调整优化，例如不能改变特定位的强度值、未能考虑到脉冲激光器的储能时间导致发射序列失真，从而限制了系统的性能的提升甚至使得光子计数激光雷达无法正常工作。

在反演目标距离时，首先应通过接收系统获取充足的光子信号从而重建出回波编码信号。为了确定光子信号的飞行时间，需要对发射的伪随机编码信号与接收编码信号做相关，通过相关峰来判定出射激光与回波之间的延迟。然而传统方法计算相关步骤效率很低，尤其是当编码长度较长的时候将占用大量计算资源而且解算速度将成为系统性能提升的瓶颈。

故探索一套适用于光子计数激光雷达的最优伪随机编码序列生成方法以及伪随机编码相关快速解算方法是提升系统性能的当务之急。

技术实现要素：

本发明的目的是提供一种适用于光子计数激光雷达的最优伪随机编码序列的生成及解码方法，以解决传统伪随机编码缺乏强度信息、容易被干扰、难以产生特定长度的序列以及难以根据实际情况对最优编码进行调整等缺点。与其他类似算法相比，本发明具有整数编码、收敛较快、不易产生非法解等优点。在目标距离反演模块，采用快速傅立叶变换算法解算相关步骤，大大提高了运算速度。

本发明的技术解决方案是提供一种基于光子计数激光雷达的最优编码生成及解码方法，包括以下步骤：

步骤一、根据激光雷达系统参数预设相关参数，相关参数主要根据设计的最大探测距离、激光器重频等共同决定。

包括：编码长度、调制比例、缓冲位数、强度范围以及粒子群算法参数；

其中粒子群算法参数包括：学习因子、惯性权重、种群规模、最大进化代数以及收敛阈值；

步骤二、获得多相伪随机编码；

2.1)随机产生长度为设定编码长度的随机数序列，并赋值给一个向量，对该向量中的每个元素就近取整，将取整后的向量作为粒子群算法中粒子的初始化的位置向量；

2.2)随机产生长度为设定编码长度的随机数序列，并赋值给一个向量，对该向量中的每个元素就近取整，将取整后的向量作为粒子群算法中粒子的初始飞行速度向量；

步骤三、获得粒子群的初始种群；

重复步骤二，分别记录每一次的位置向量和速度向量，获得符合设定种群规模的多相伪随机编码，构成粒子群算法中粒子群的初始种群；

步骤四、获得最优编码；

4.1)依据光子计数激光雷达对编码的要求设计适应度函数；上述适应度函数应包括对探测环境中存在的干扰的模拟以及对优良特性的奖励项与非法解的惩罚项；对干扰的模拟可以包括时间抖动、随机噪声和大气干扰等，惩罚项包括强度值超范围、缓冲位数不足等非法情况。

4.2)根据得到的适应度函数计算步骤三得到的初始种群中每个粒子的适应度；选取适应度值最好的粒子作为初始最优粒子；

4.3)通过粒子群算法的迭代进化公式更新初始粒子群中的每个粒子的位置向量，并根据适应度函数计算更新后每个粒子的适应度，记录适应度最高的粒子，并与历史最优粒子适应度比较，选取全局最优粒子；

4.4)重复步骤4.3)，直到满足提前设置的最大进化代数，获得的全局最优粒子对应的位置向量即为最优编码；

步骤五、通过光子计数激光雷达获取发射编码与接收编码，所述发射编码即为步骤四获得的最优编码；再对发射编码与接收编码做相关，从而解算出目标距离。

优选地，步骤4.3)具体为：

4.31)根据粒子群算法速度更新公式更新粒子飞行速度向量，对飞行速度向量就近取整，再通过就近取整后每个粒子的飞行速度向量更新粒子群的初始种群中每个粒子的位置向量；

4.32)计算更新后的粒子种群中每个粒子的适应度值，若该粒子本次更新位置的适应度比该粒子的历史最优粒子对应的适应度更高，则以该粒子本次更新的位置向量为该粒子的历史最优值；

4.33)若该粒子的历史最优粒子的位置向量的适应度大于全局最优粒子的位置向量的适应度，则以该粒子的历史最优粒子的位置向量替换全局最优粒子的位置向量；

4.34)根据预设的种群规模与最大进化代数循环步骤4.31)到步骤4.33)，粒子群进化到最大进化代数，输出全局最优值为最优编码。

优选地，步骤4.31)具体通过公式(1)更新飞行速度向量，

式中，上标中的k表示当前迭代的代数，v为速度向量，x为位置向量，w为惯性权重，c1，c2为学习因子，s为种群规模，gbest全局最优粒子的位置向量，psbest历史最优粒子的位置向量，r1、r2为在[0，1]内的随机数；

根据下式更新位置向量：

优选地，上述步骤五具体为：

5.1)通过光子计数激光雷达获取发射编码与接收编码；

5.2)通过fft算法分别对发射编码与接收编码作离散傅立叶变换；

5.3)对接收编码的离散傅立叶变换求共轭；

5.4)通过发射编码与接收编码的离散傅立叶变换的共轭求相关函数的傅立叶变换；

5.5)对相关函数的傅立叶变换作傅立叶逆变换，通过相关函数的相关峰求得光子飞行时间；

5.6)通过光子飞行时间与光速即可获得目标距离。

本发明的有益效果是：

1、本发明编码方法中编码长度可调且编码形式不固定，与其他伪随机编码序列相比，该方法能够获得光子计数探测环境下性能更加优异的编码序列，通过该编码对信号进行调制后，产生的信号频谱宽，抗干扰能力强；

2、根据光子计数激光雷达的实需求构建粒子适应度函数，作为伪随机序列的评价表标准，获得的伪随机序列的性能更好；

3、本发明伪随机编码为多相伪随机编码，编码序列中有多个强度值，获得更高的相关增益；

4、与其他类似算法相比，本发明采用粒子群算法并就近取整，避免了大量的非法解，具有整数编码、收敛较快、不易产生非法解等优点；

5、在目标距离反演模块，采用快速傅立叶变换算法解算相关步骤，大大提高了运算速度。

附图说明

图1是基于光子计数激光雷达的最优编码生成算法流程图；

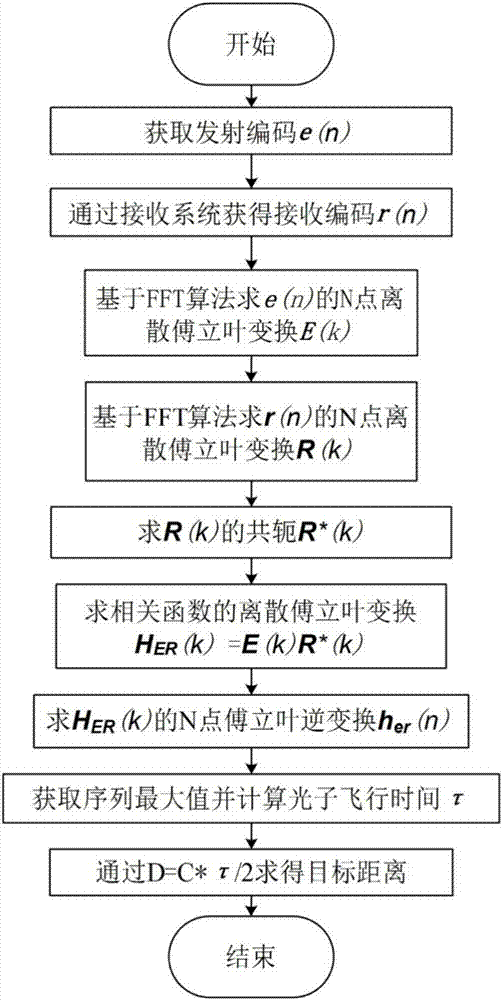
图2是解码过程流程图；

图3是本发明最优编码生成算法生成的编码序列的自相关性展示；

图4是m序列的自相关性展示；

图5是本发明解码计算相关与传统方法计算相关所耗费时间的对比图。

具体实施方式

以下结合附图及具体实施例对本发明做进一步的描述。需要说明的是说明书中加粗符号代表向量，未加粗符号代表数值。

如图1本发明最优编码生成方法如下：

步骤一：根据光子计数激光雷达系统设置伪随机编码序列长度ls、调制比例、缓冲位数、强度范围；

步骤二：设置粒子群算法参数：学习因子c1，c2，惯性权重w，种群规模s以及最大进化代数mg；

步骤三：随机产生一个长度为ls的随机数序列，并赋值给向量x；

步骤四：对向量x中的每个元素就近取整，若元素则

将该向量x作为粒子群中粒子的初始化的位置向量；

步骤五：随机产生一个长度为ls的随机数序列，并赋值给向量v；

步骤六：对向量v中的每个元素就近取整，作为粒子群中粒子的初始化的速度向量；

步骤七：重复步骤三至步骤六s次，分别记录每一次的位置向量和速度向量，获得符合设定种群规模的多相伪随机编码，构成粒子群算法中粒子群的初始种群；

步骤八：将每一次的位置向量xs赋值给psbest，作为当前每个粒子的历史最优值；

步骤九：根据光子计数激光雷达对编码性能的需求构建粒子适应度函数；所述适应度函数应包括对探测环境中存在的干扰的模拟以及对优良特性的奖励项与非法解的惩罚项；对于代表编码具有良好性能的计算项取较大的奖励因子，作为粒子群进化的方向；对于代表编码为非法解的计算项取较大的惩罚因子，作为禁止搜索区域；

适应度函数可以写成以下形式：

其中ep表示具有良好性能的计算项，np表示非法解的计算项。a与b分别表示奖励因子与惩罚因子。以最大化适应度为进化方向。lep与lnp分别表示具有良好性能的计算项与非法解的计算项的个数。

例如ep可以设计为相关结果中的最高峰与次高峰的比值，作为自相关性的度量；又例如设计np时需将编码强度不在强度范围内的情况纳入考虑，即统计整个编码中强度不在强度范围内的个数。

步骤十：计算粒子种群中每个粒子的适应度函数值fitnesss；

步骤十一：选取种群中适应度最高的粒子为当前全局最优粒子，其对应的位置向量为gbest；

步骤十二：根据下式更新速度向量：

上标中的k表示当前迭代的代数；

步骤十三：根据下式更新位置向量：

步骤十四：若更新的粒子的适应度大于psbest，则以为该粒子的历史最优粒子的位置向量psbest；

步骤十五：若该粒子的历史最优粒子psbest的适应度大于全局最优粒子的位置向量gbest的适应度，则以该粒子的历史最优粒子psbest为全局最优粒子的位置向量gbest；

步骤十六：重复步骤十二至步骤十五s次，遍历整个种群；

步骤十七：重复步骤十六mg次；

步骤十八：输出全局最优粒子gbest为最终输出最优编码a(n)；

如图2，本发明解码方法如下：

步骤十九：将编码信号a(n)通过激光器转化为光信号并重复发射若干次，再由接收系统接收回波光子，累积并量化后获得接收编码序列b(n)；将接收序列重新映射回强度区间，重新映射后即可获得和发射序列类似的序列；

步骤二十：基于快速傅立叶变换算法(fft)求发射伪随机序列a(n)的n点离散傅立叶变换

其中a(k)表示离散傅里叶变换之后的信号，dft(·)表示做离散傅里叶变换，n表示离散傅里叶变换的序列长度，表示复指数，即

步骤二十一：基于快速傅立叶变换算法(fft)求接收伪随机序列b(n)的n点离散傅立叶变换

步骤二十二：求接收序列离散傅立叶变换b(k)的共轭b*(k)，

步骤二十三：求相关函数的离散傅立叶变换hab(k)＝a(k)b*(k)

步骤二十四：对相关函数的离散傅立叶变换hab(k)做n点傅立叶逆变换ifft，

步骤二十五：求序列hxy的最大值，设最大值所在位置为d，系统时间分辨率为tbin，则发射序列与接收序列之间的延迟τ＝d*tbin。

步骤二十六：用c表示光速，根据下公式求得最终测距距离d：

图3、图4中横轴为回波编码信号与发射编码信号的相对延迟，纵轴为不同回波位置的相关幅值，通过图3与图4对比可以发现本发明提出的基于光子计数激光雷达的最优编码生成算法所产生的编码自相关性更加优异，相关峰峰值高于其他位置的相关值十倍以上，远胜m序列；本次测试中，适应度函数设计了强度值超范围、调制位置数不满足设定比例、不满足激光器缓冲时间三个非法解的惩罚项，取较大的惩罚因子(本测试中取1*10^(20))；并设计了相关峰峰值与其余相关值之比的奖励项，取较大的奖励因子(本测试中取1*10^(10))。用于测试的编码长度均为16383位，图3的编码为粒子群算法进化1000代得到的结果。

图5是本发明fft算法计算相关与传统方法计算相关所耗费时间的对比图。下方较粗的线条为fft算法随编码长度增大所耗费时间的曲线。显然fft算法计算相关所耗费的时间更少，并且消耗的时间不随编码长度增大而急剧增多，应注意本坐标系为对数坐标。

注：用于此次测试的工具为matlab2016a，测试用计算机为联想thinkcentrem8600t-d064。