基于电磁涡旋波的三维合成孔径雷达成像方法与流程

本发明属于雷达技术领域，更进一步涉及雷达成像技术领域中的合成孔径雷达(syntheticapertureradar，sar)三维成像方法。

背景技术：

合成孔径雷达因具有全天时、全天候、远距离成像的能力，在战略防御、地形测绘等军用和民用领域得到了广泛应用。传统sar仅能获取斜平面上的两维图像，且受叠掩和透视收缩等的影响。为了克服两维成像的缺陷，国内外学者提出了多种三维sar成像的方法。目前三维sar成像已成为现代雷达的研究热点之一。

下视线性阵列三维sar系统作为实现三维sar成像的主要技术之一，目前已受到各国学者的关注。通过利用垂直航向的线性阵列，下视线性阵列三维sar可实现除传统sar成像可得到的沿航向和距离向分辨以外，还能获得垂直航向的分辨能力，从而实现对照射场景的三维成像。但是，下视线性阵列三维sar存在两个主要的问题：垂直航向分辨率受阵列尺寸的影响，与沿航向和距离向分辨率相比通常较低；为避免模糊图像，垂直航向上的阵元间距必须足够小，从而导致阵元数的大大增加。

电磁涡旋波携带的轨道角动量(orbitalangularmomentum,oam)受到了无线通信，射电天文学等越来越多领域的重视。近年来，电磁涡旋波被成功运行于二维雷达目标成像。但是目前的研究局限于雷达与目标相对静止，且仅能获取目标的两维图像。

技术实现要素：

本发明针对上述三维sar成像的问题，提出了一种新的基于电磁涡旋波的三维sar成像方法。与传统方法不同，本发明充分利用雷达与目标的相对运动，在传统两维sar成像的基础上，结合电磁涡旋波携带的oam获取目标的第三维图像，从而得到三维sar图像。

为实现上述目的，本发明的主要步骤如下：

(1)发射具有不同oam态的电磁涡旋波；

(2)对接收到的回波信号进行距离压缩和距离徙动校正；

(3)沿航向进行去斜操作，得到沿航向聚焦图像；

(4)以场景中心为参考，对沿航向聚焦后的图像进行多普勒单元徙动校正；

(5)在oam域进行傅里叶变换，得到三维图像，再根据角度转换关系，得到最终的三维sar图像。

本发明与现有的技术相比具有以下优点：

本发明利用电磁涡旋波携带的oam和雷达与场景间的相对运动，克服了传统方法仅能实现二维成像的局限，最终可得到三维sar图像。

附图说明

图1为本发明的设计方法流程图；

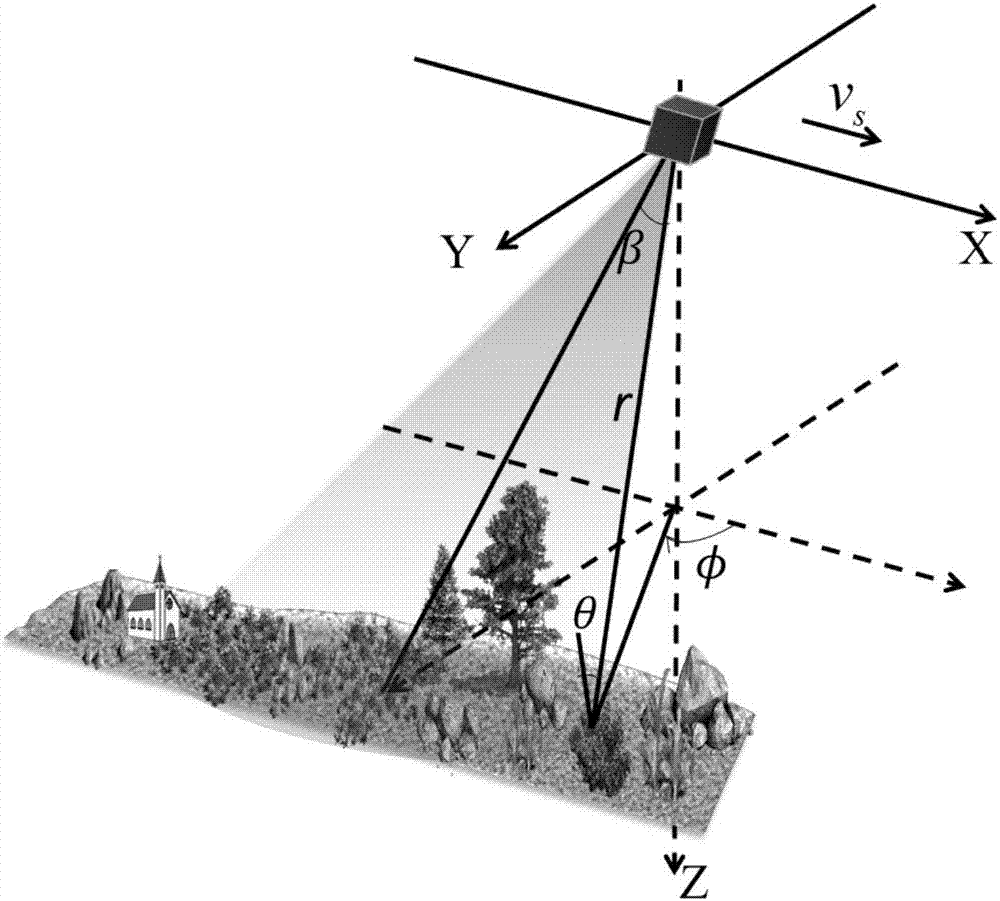
图2为sar系统的成像几何示意图；

图3为利用本发明方法得到的三维sar图像；

图4为利用本发明方法得到的第二个点目标的沿锥角方向和沿方位角方向的成像剖面图；

具体实施方式

参照附图1，本发明的具体实施步骤如下：

步骤1，发射具有不同oam态的电磁涡旋波。

目前有若干种oam产生和发射的方式，本发明以均匀圆阵为例，经过适当的辐射波形调整，第n个阵元发射的线性调频信号为

其中，τ表示距离快时间，l为oam模态数，al为发射oam态为l的信号幅值，nl为生成oam态为l的信号所需的阵元数，wr为距离包络，fc为载频，γr为距离线性调频率，为第n个阵元的调制相位。

步骤2，将接收到的回波信号进行距离压缩和距离徙动校正。

系统成像几何示意图如附图2所示，雷达以速度vs沿x轴方向运动，r为雷达至场景中某一目标的斜距，β，θ和φ分别表示锥角，入射角和方位角。假设观测场景中有一点目标，其极坐标位置为(r0,θ0,φ0)，相应的直角坐标位置为(x,y,z)，零时刻雷达的坐标位置(0,0,0)，时刻t为(vst,0,0)。为简单起见，忽略噪声，对所有阵元接收回波进行累加解调后为

其中，σ为目标的后向散射系数，jl(·)为第一类l阶贝塞尔函数，k＝2π/λ为波数，λ＝c/fc为波长，c为电磁波传播速度，al为生成oam态为l的圆阵半径，wa为沿航迹方向包络，t0＝x/vs。r(t)为雷达至目标的瞬时斜距，其值为

为零多普勒时刻斜距。φ(t)为瞬时方位角，且有φ(0)＝φ0。根据成像几何关系，易知

其中，β(t)为瞬时锥角，且有β(0)＝β0。对于低斜视成像说，瞬时方位角也可写为

由此可将接收回波重写为

其中，为沿航向调频率。

对接收回波信号进行传统距离压缩和距离徙动校正后为

其中，pr(τ)为距离压缩后的脉冲包络，τc＝2rc/c。

步骤3，沿航向进行去斜操作，得到方位聚焦图像。

对距离压缩后的信号沿时间域t进行去斜操作，可得

再对上式沿时间域t进行傅里叶变换，可得

其中，ft为多普勒频率，pa(ft)为沿航向压缩脉冲包络。至此，已获取距离向和沿航向的压缩图像。由上式可知，oam态l与多普勒频率ft相互耦合，目标在多普勒域的聚焦位置随着l的不同而不同。

步骤4，以场景中心为参考，对沿航向聚焦后的图像进行多普勒单元徙动校正。

与距离单元徙动类似，这里将多普勒聚焦位置随oam的变化称为多普勒单元徙动，其徙动量为可以看出，多普勒单元徙动量由oam，平台速度，斜距和入射角决定。对于给定的l和rc，仅θ0未知。通常情况下，场景中心的入射角θc可以根据系统参数估计得到，而与多普勒分辨率相比，可以忽略，因此可以利用场景中心为参考进行多普勒单元徙动校正。多普勒单元徙动校正后可得

步骤5，在oam域进行傅里叶变换，得到三维图像，再根据角度转换关系，得到最终的三维sar图像。

对多普勒单元徙动校正后的回波信号沿oam域进行傅里叶变换可得

其中，pl(fl)为方位角压缩脉冲包络。考虑到上式也可写为

由此便得到了目标场景的三维sar图像。

下面结合仿真数据实验对本发明的效果做进一步的说明。

1、仿真条件：

三维sar成像系统的仿真参数如下表所示，并假设在场景中有三个点目标。

三个点目标对应的锥角和方位角分别为(2.66°,86.8°)，(0.87°,88.9°)和(-0.85°,90.97°)

2、仿真数据包实验分析：

利用本发明提出的方法，对接收回波进行三维sar成像后的结果如附图3所示，可以看出三个点目标得到了很好的区分，且聚焦位置与真实位置一致。为进一步给出聚焦效果说明，附图4(a)和(b)分别给出了第二个点目标的沿锥角方向和沿方位角的剖面图，可以看出，目标实现了很好的聚焦。