一种封闭空间面板声学贡献度识别方法与流程

本发明涉及噪声源识别方法领域，特别涉及一种基于正交球面波叠加的封闭空间面板声学贡献度识别方法。

技术背景

由复杂弹性封闭空腔结构在外界激励下，振动而形成的空间声场是工程实际中最具代表性的一类声场，如汽车、船舶和飞机的舱内声场。随着人们对于生活、工作环境的舒适性要求不断提高，封闭空间结构内部的噪声问题被人们所日益重视。外界激励能量传递至封闭空腔结构后，各面板振动进而向声腔内辐射结构噪声，最终影响封闭空间内部，其声场特性的主要因素是组成声腔的所有板件的振动和声学特性。对构成封闭结构的各个面板进行声学贡献度分析，有针对性地选择和优先控制对内声场影响较大的面板，是取降低噪声设计与声学优化的关键。

现有的封闭空间面板声学贡献度识别方法，主要包括两类：(1)基于有限元/边界元法建模方法。1995年zhang基于声学边界元模型，提出了封闭空腔周围面板对空腔内某一场点噪声响应的贡献量计算方法。2000年mohanty利用有限元和边界元的数值方法计算空间声场的面板声学贡献度。2002年ding基于有限元数值方法并结合声学互易性测量原理，提出了弹性封闭薄板声腔的局部面板振动对内部声场的声学贡献度算法。2007年wolff提出了基于kirchhoff积分公式的封闭空间声场面板声学贡献度算法。2009年han引入“声学贡献和”、“声学贡献比”以及“声场总贡献”的概念提，出了一种适用于多特征场点多响应峰值的面板声学贡献分析方法。2010年赵静提出通过声学有限元方法获得结构振动响应，并以此作为声学边界元模型边界条件的面板声学贡献识别方法。2016年李苏平基于车身结构-声场有限元耦合模型，利用virtual.lab商业软件进行面板声学贡献分析。该类方法的计算精度，很大程度上依赖于模型所划分单元的精细程度以及边界条件简化的程度，同时存在计算量庞大，计算效率较低的问题。(2)基于近场声全息技术。2006年hald提出了基于统计最优近场声全息测量的面板声学贡献度识别方法，该方法利用双面阵列测量封闭空间内声场中各振动面板的近场声学信息，再通过体积速度声源进行互易性测量获得传递函数，从而识别出封闭空间结构中任意振动面板的声学贡献度。该方法只需对感兴趣的面板进行一次局部近场声全息测量，就可得到该部位对声场的声学贡献，而不必进行全场测量，具有较好灵活性，但由于仍要进行传递函数的互易性测量，存在工作量巨大的问题。2013年wu提出了基于helmholtz最小二乘法的近场声全息的面板声学贡献度识别方法。该方法利用近场声全息测量技术，通过对复杂振动结构表面的振动声学响应进行重建，获得振动面板的表面声强，建立起每个面板的声功率流与指定场点的声压级之间的联系。但由其算法定义得到的面板声学贡献度由于没有正负属性，因此在实际应用中均具有一定的局限性。2015年，肖悦基于等效源法的内部近场声全息技术，提出了一种能够识别复杂形状封闭空腔结构内声场的面板声学贡献度的计算方法。该方法通过一组全息声压测量来重建整个声场信息，利用声场等效原理求解出封闭结构各振动面板对腔体内任意位置的声学贡献度，具有参数意义明确的特点，但该方法需要完成对整个封闭空间的全场的声学测量，要求布置的测点数较多，增加了测量成本，同时存在等效源位置选取的问题。

技术实现要素：

本发明所解决的技术问题是避免上述现有技术所存在的不足，提供一种基于正交球面波叠加的封闭空间面板声学贡献度识别方法，简化了计算过程，提高波源的源强列向量计算精度。

本发明解决其技术问题所采用的技术方案如下。一种封闭空间面板声学贡献度识别方法，其特点在于，包括以下步骤：

1)在封闭空间内部中设置贴近内表面的全息测量面，测量面上呈网格式设置声压传感器，相邻网格点之间的距离小于半个波长，所述的声压传感器用于测量位于测量面上的声压值；

2)利用正交球面波叠加法，建立测量面声压与正交球面波源的源强之间的传递关系，计算正交球面波源的源强；具体步骤如下：

2.1在封闭空间内部任意选取一点作为原点建立球坐标系，以此点作为波源位置；坐标系的x轴、y轴和z轴的正方向满足右手定则，坐标系的原点选为封闭空间几何中心；

2.2根据正交球面波叠加原理，将封闭空间结构板件振动形成的内部稳态声场等效为由一系列不同阶次、不同强度的正交球面波源产生的声场，则在所述坐标系下声场中任意位置r＝(r,θ,φ)处的声压可表示为：

式(1)中：r为正交球面波源所在位置与声场中任意点之间的距离，θ为距离矢量r与z轴正方向之间的夹角，为r与x轴正方向之间沿逆时针方向的夹角，为球谐函数，为连带legendre函数；系数j、m和n之间的关系可以描述为j＝n²+n+m+1；n为选取的正交球面波源展开项数的截断阶数；正交球面波总阶数j与截断阶数n的关系为j＝(n+1)²；jn(kr)为第一类球bessel函数；为对应(n,m)阶正交球面波产生的声压；cj与(n,m)阶正交球面波源的源强cnm相对应；

2.3建立测量面声压与正交球面波源的源强之间的传递关系如下：

ph＝ψphc(2)

式(2)中：ph＝[p(rh,1),p(rh,2),…,p(rh,m)]^t为全息面上m个测量点的声压列向量，为各阶正交球面波源到全息面上各测量点的传递矩阵，c＝[c1,c2,…,cj]^t为对应于各阶正交球面波源的源强组成的列向量；

2.4根据式(2)，满足全息面上的测量点数m大于正交球面波阶数j，采用奇异值分解技术唯一确定正交球面波源的源强：

c＝(ψph)⁺ph(3)

式(3)中：上标“+”表示矩阵的广义逆；

3)根据正交球面波源的源强，建立封闭空间结构表面法向振速与正交球面波源的源强之间的传递关系：

vs＝ψvsc(4)

式(4)中：vs为封闭空间结构表面法向振速列向量，ψvs为j阶正交球面波源与振动结构表面质点振速之间的传递矩阵：

式(5)中：ρ为介质密度，c为介质中的声音传播速度，k＝ω/c为声波波数，ω为角频率，为虚单位，s为封闭空间结构表面节点个数；

4)联合式(3)和(4)，建立封闭空间结构表面法向振速与测量面声压之间的传递关系，可以得到封闭空腔结构表面法向振速列向量：

vs＝ψvs(ψph)⁺ph(6)

5)利用声场等效原理，计算封闭空间面板声学贡献度；具体步骤如下：

5.1根据声场等效原理，封闭空间内声场中任意一点处的声压可以认为是由于组成该封闭空间的所有面板振动而在该处引起的声压相互叠加产生的，表示为：

式(7)中：pfp为封闭空间内部声场中任意场点r处的声压，pk为由第k个面板振动而在r处引起的声压分量，k＝1,2,…,k，k为构成整个封闭振动结构的面板个数；

5.2根据式(1)，将封闭空间内部声场中任意场点r处的声压表示为：

pfp＝ψpc(8)

式(8)中：ψp＝[ψp,1(rfp),ψp,2(rfp),…,ψp,j(rfp)]为j阶正交球面波源与场点r处声压之间的传递矩阵；

将由第k个面板振动而在封闭空间内部声场中在该场点处引起的声压分量表示为：

pk＝ψpck(9)

式(9)中：ck为第k个面板对应的正交球面波源的源强列向量；

5.3对于由所有结构面板振动形成的封闭声场，根据式(4)，将正交球面波源的源强列向量表示为：

式(10)中：为封闭空间结构的表面法向振速列向量，vsk为第k个面板的法向振速向量；

5.4根据封闭空间面板声学贡献的物理意义，由第k个面板振动在某场点处产生的声压可以认为是第k个面板单独振动而其他面板的法向振速为零时的情况，根据式(10)得到第k个面板对应的正交球面波源的源强列向量：

5.5联合(9)和式(11)，建立由第k个面板振动而在封闭声腔内场点处引起的声压分量与第k个面板表面法向振速的关系为：

5.6根据式(5)，将ψvs表示为：

式(13)中：pk为封闭空间结构第k个面板上所有节点个数，其排列顺序为rk,1,,rk,2,…,rk,pk，且满足ψsvk可表示为：

5.7联合式(6)和式(13)，建立第k个面板表面法向振速与测量面声压的关系为：

5.8联合式(12)和式(18)，建立由第k个面板振动而在封闭声腔内场点处引起的声压分量与测量面声压的关系为：

5.9联合式(8)和式(16)计算封闭空间第k个面板对内部声场的声学贡献度：

式(17)中：re表示取实部，上标“*”表示复共轭。

与已有技术相比，本发明有益效果体现在：

1、正交函数展开项数比传统的有限元/边界元法中离散点数要少得多，避免了繁琐的奇异值处理及解的非唯一性问题，求解效率高，对测点位置和重建点位置没有任何限制，可适应于任意形状的封闭声场，所需的测点数量少。

2、通过近场全息测量来重建整个声场和面板振动信息，避免了复杂声振系统的声辐射及其耦合作用的计算，简化了计算过程；

3、采用的正交球面波源的不同阶次具有相互正交性，以此来构造的传递矩阵的列向量之间是线性无关的，即传递矩阵是列满秩的，降低了传递矩阵的病态性，有利于提高波源的源强列向量计算精度。

4、采用正交球面波源可在在封闭空间内部的任意一点处设置，实施简单方便。

总之，可适应于任意形状的封闭声场，且所需的测点数量少，实施简便。由于采用的正交球面波源的不同阶次具有相互正交性，降低了传递矩阵的病态性，大大提高了计算精度。

附图说明

图1为本发明采用的球坐标系示意图；

图2为本发明实施例的封闭空间结构模型示意图；

图3为本发明实施例的封闭空间内声场观测点声压值的结果比较；

图4(a)为本发明实施例在峰值频率46hz处封闭空间各面板的声学贡献度比较结果；

图4(b)为本发明实施例在峰值频率82hz处封闭空间各面板的声学贡献度比较结果。

具体实施方式

以下结合附图和实施例对本发明作进一进说明。参见图1至图4(b)，一种封闭空间面板声学贡献度识别方法，具体步骤如下：

a、在封闭空间内部中设置贴近内表面的全息测量面，测量面上呈网格式设置声压传感器，相邻网格点之间的距离小于半个波长，所述的声压传感器测量位于测量面上的声压值；

b、利用正交球面波叠加法，建立测量面声压与正交球面波源的源强之间的传递关系，计算正交球面波源的源强；

所述步骤b具体步骤如下：

b1、在封闭空间内部任意选取一点作为原点建立球坐标系，以此点作为波源位置。坐标系的x轴、y轴和z轴的正方向满足右手定则，优选地，所述坐标系原点选为封闭空间几何中心，如图1所示；

b2、根据正交球面波叠加原理，将封闭空间结构板件振动形成的内部稳态声场等效为由一系列不同阶次、不同强度的正交球面波源产生的声场，则在所述坐标系下声场中任意位置r＝(r,θ,φ)处的声压可表示为：

式(1)中：r为正交球面波源所在位置与声场中任意点之间的距离，θ为距离矢量r与z轴正方向之间的夹角，为r与x轴正方向之间沿逆时针方向的夹角，为球谐函数，为连带legendre函数；系数j、m和n之间的关系可以描述为j＝n²+n+m+1；n为选取的正交球面波源展开项数的截断阶数；正交球面波总阶数j与截断阶数n的关系为j＝(n+1)²；jn(kr)为第一类球bessel函数；为对应(n,m)阶正交球面波产生的声压；cj与(n,m)阶正交球面波源的源强cnm相对应；

b3、建立测量面声压与正交球面波源的源强之间的传递关系如下：

ph＝ψphc(2)

式(2)中：ph＝[p(rh,1),p(rh,2),…,p(rh,m)]^t为全息面上m个测量点的声压列向量，为各阶正交球面波源到全息面上各测量点的传递矩阵，c＝[c1,c2,…,cj]^t为对应于各阶正交球面波源的源强组成的列向量；

b4、根据式(2)，满足全息面上的测量点数m大于正交球面波阶数j，采用奇异值分解技术唯一确定正交球面波源的源强：

c＝(ψph)⁺ph(3)

式(3)中：上标“+”表示矩阵的广义逆；

c、根据正交球面波源的源强，建立封闭空间结构表面法向振速与正交球面波源的源强之间的传递关系：

vs＝ψvsc(4)

式(4)中：vs为封闭空间结构表面法向振速列向量，ψvs为j阶正交球面波源与振动结构表面质点振速之间的传递矩阵

式(5)中：ρ为介质密度，c为介质中的声音传播速度，k＝ω/c为声波波数，ω为角频率，为虚单位，s为封闭空间结构表面节点个数；

d、联合式(3)和(4)，建立封闭空间结构表面法向振速与测量面声压之间的传递关系，可以得到封闭空腔结构表面法向振速列向量：

vs＝ψvs(ψph)⁺ph(6)

e、利用声场等效原理，计算封闭空间面板声学贡献度。

所述步骤e具体步骤如下：

e1、根据声场等效原理，封闭空间内声场中任意一点处的声压可以认为是由于组成该封闭空间的所有面板振动而在该处引起的声压相互叠加产生的，表示为：

式(7)中：pfp为封闭空间内部声场中任意场点r处的声压，pk为由第k个面板振动而在r处引起的声压分量，k＝1,2,…,k，k为构成整个封闭振动结构的面板个数；

e2、根据式(1)，将封闭空间内部声场中任意场点r处的声压表示为：

pfp＝ψpc(8)

式(8)中：ψp＝[ψp,1(rfp),ψp,2(rfp),…,ψp,j(rfp)]为j阶正交球面波源与场点r处声压之间的传递矩阵。

将由第k个面板振动而在封闭空间内部声场中在该场点处引起的声压分量表示为：

pk＝ψpck(9)

式(9)中：ck为第k个面板对应的正交球面波源的源强列向量。

e3、对于由所有结构面板振动形成的封闭声场，根据式(4)，将正交球面波源的源强列向量表示为：

式(10)中：为封闭空间结构的表面法向振速列向量，vsk为第k个面板的法向振速向量。

e4、根据封闭空间面板声学贡献的物理意义，由第k个面板振动在某场点处产生的声压可以认为是第k个面板单独振动而其他面板的法向振速为零时的情况，根据式(10)得到第k个面板对应的正交球面波源的源强列向量：

e5、联合(9)和式(11)，建立由第k个面板振动而在封闭声腔内场点处引起的声压分量与第k个面板表面法向振速的关系为：

e6、根据式(5)，将ψvs表示为：

式(13)中：pk为封闭空间结构第k个面板上所有节点个数，其排列顺序为rk,1,,rk,2,…,rk,pk，且满足ψsvk可表示为：

e7、联合式(6)和式(13)，建立第k个面板表面法向振速与测量面声压的关系为：

e8、联合式(12)和式(18)，建立由第k个面板振动而在封闭声腔内场点处引起的声压分量与测量面声压的关系为：

e9、联合式(8)和式(16)计算封闭空间第k个面板对内部声场的声学贡献度：

式(17)中：re表示取实部，上标“*”表示复共轭。

本发明方法的检验：

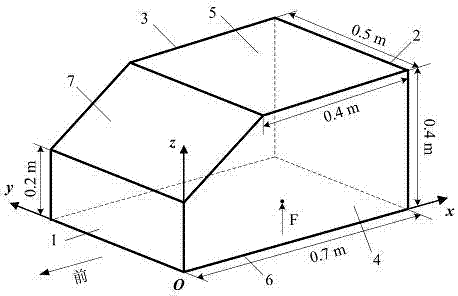
为了验证基于正交球面波叠加的封闭空间面板声学贡献度识别方法，选取类似车厢结构的不规则封闭空间内部声场为分析对象，如图2所示。该封闭结构由前侧板1、后侧板2、左侧板3、右侧板4、顶板5、底板6和上斜板7组成。封闭空间结构的各面板厚度均为2mm，材料为薄钢板，材料密度为7.8×10³kg/m³，弹性模量为210gpa，泊松比为0.3，系统阻尼比0.01，整个结构受到来自底面的幅值为0.2n、频带20～250hz的激励，激励点位置为(0.388m,0.235m,0)。模型底板6的四个角点固定，在封闭空间内选取点(0.3m,0.3m,0.3m)作为声压观测点。

由于该封闭空间结构的形状不规则，无法用解析式进行描述，因此采用声学软件lmsvirtual.lab利用耦合声学有限元法进行声场计算，将得到的全息面上各测点的声压值作为进行内部nah重建的“输入量”，并加入信噪比为30db的随机噪声以更接近实际情况。将腔体内部的全息面上的仿真声压作为“测量”数据，利用本发明方法进行声场预测和面板声学贡献度计算，并将计算结果与采用耦合声学有限元法进行对比。

图3为分别采用本发明方法和耦合声学有限元法计算的封闭空间内声场观测点声压的对比结果，可以看出两者的吻合程度非常好，说明本发明方法能够准确有效地预测由振动结构形成的封闭空间内声场。

图4(a)和图4(b)为分别采用本发明方法和耦合声学有限元法计算的在46hz和82hz这两个响应的峰值频率处的封闭空间各面板声学贡献度。可以看出，在峰值频率46hz和82hz处，采用两种方法计算获得的各个振动面板的声学贡献度都具有较高的一致性，这说明本发明方法能够准确地识别出各面板的声学贡献度。同时，本发明方法提出的声学贡献度定义算法既能够提供声学贡献的正负属性，又能与内部声场中的任意场点的声压值相互关联，具有较好的优越性，可为结构声学优化设计和治理提供更有针对性的依据。