一种基于等效电路的锂离子电池SOC估计算法的制作方法

本发明属于检测领域，具体涉及一种锂离子电池荷电状态的估算方法。

背景技术：

近年，全球的汽车数量急剧攀升，对能源的需求也越来越大，同时对环境造成的污染也愈发严重。新能源汽车，尤其是电动汽车已成为未来汽车的发展方向，但其发展速度仍受着动力电池及其应用技术的制约。如何延长电池的使用寿命、提高电池的能量效率及可靠性，是电动汽车产业化必须解决的问题，因此研究电池管理技术具有十分重大的意义。

动力电池荷电状态(stateofcharge)简称soc。锂离子电池的剩余电量是电池在运行过程中最重要的性能参数之一，剩余电量的估计是一个不可忽视的环节。对于电动车来说，准确地估计电池的soc，不仅可以提高续航能力，还可以延长电池寿命，提高安全性。

技术实现要素：

针对本领域存在的不足之处，本发明公开了一种基于等效电路的锂离子电池soc估计算法，以准确地估计电池的soc。

实现本发明上述目的技术方案为：

一种基于等效电路的锂离子电池soc估计算法，包括步骤:

s1、在不同的温度下，获取开路电压uocv与soc及温度t的关系，

s2、建立等效电路模型，获取所述模型参数与所述soc及温度t的关系，该步骤具体为

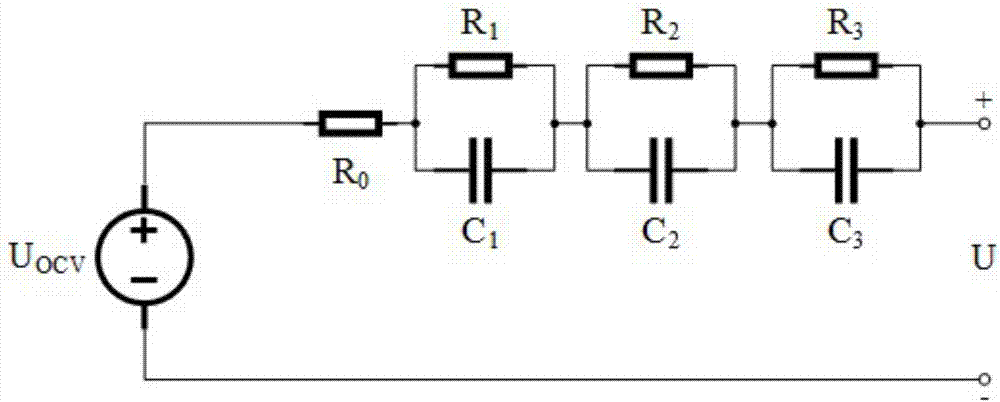
s21、建立三阶等效电路模型，等效电路内包含串联的欧姆电阻r0和三个rc单元，每个rc单元由并联的电阻和电容组成；确定所述等效电路端电压u与开路电压uocv的特性关系；

s22、获取所述等效电路模型中的欧姆内阻r0与soc及温度t的关系：确定脉冲放电结束瞬间的电压特性。

s222、获取温度t下欧姆内阻r0与soc的关系

s223、获得其它温度下欧姆内阻r0与soc的关系

s23、获取所述等效电路模型中的rc单元参数r1，c1，r2，c2，r3，c3与soc及温度t的关系；

s231、测定脉冲放电结束瞬间后的等效电路的电压u(t)；

s232、获取相同温度下rc单元参数r1，c1，r2，c2，r3，c3与soc的关系。

s233、获取其它温度下并联rc单元参数r1，c1，r2，c2，r3，c3与soc的关系。

s3、估计当前温度t和电池运行的时间t下的soc值，包括s31、简化电压特性方程，s32、对电压特性方程进行求解。

其中，步骤s1中，获取一系列温度t下开路电压uocv与soc的关系，t的温度范围为-10～50℃，soc为0.1～0.9范围内的至少9个值。

进一步地，将温度t下开路电压uocv与soc的关系以五阶多项式表达：

uocv＝a0+a1soc+a2soc²+a3soc³+a4soc⁴+a5soc⁵

其中uocv表示电池开路电压，a0～a5为多项式系数，且为常数，soc为电池的荷电状态。

可选地，t在低于10℃时每4-8℃获取一组uocv与soc的关系，t在10℃以上时每8-12℃获取一组uocv与soc的关系。

其中，所述步骤s21为：

针对三阶等效电路模型，建立电池模型的特性方程：

其中，u0为所述欧姆内阻r0两端的电压，u1～u3为所述三个rc单元两端的电压，i为电流；

求解式(1)，可得等效电路端电压的表达式为：

其中，u1(0)、u2(0)和u3(0)分别为脉冲放电(hppc)计时开始时，三个rc单元两端的电压初值。

步骤s22中，脉冲放电(hppc)为已有的测试方法，脉冲放电时间、电流等均为已有的规范(例如依据freedom电池测试手册)。

根据图2的结构可知，脉冲放电结束瞬间，电压的变化完全是由欧姆内阻r0产生。因此，欧姆内阻r0采用下式获取：

式中，ul为脉冲放电结束的电压突变，i为脉冲放电电流值。

其中，所述步骤s22为：

根据温度t下，电池在不同soc下的hppc实验得到的电压响应曲线，采用式(4)计算得到不同soc下的欧姆内阻r0和r0-soc曲线。所述soc值为0.1～0.9范围内的至少9个数值。对该温度下的r0-soc曲线进行多项式拟拟合，所述多项式拟合式为：

r0＝b0+b1soc+b2soc²+b3soc³+b4soc⁴+b5soc⁵

其中r0表示欧姆内阻，b0～b5为多项式系数，且为常数，soc为电池的荷电状态。

脉冲放电结束瞬间，电流为零，图2所示电路结构为零输入响应，其电压特性方程为：

进一步地，所述步骤s231具体为：

由图2的电路结构可知，脉冲放电结束瞬间后，欧姆内阻两端的电压变为零，但三个rc单元两端的电压不会变为零。因此式(3)变为：

原则上，采用数学软件的非线性拟合工具，可以直接根据式(4)对电压响应曲线拟合，得到三个rc单元的参数值。但是，由于式(4)中存在指数函数，且图2结构中的电容的数值从几十到几百kf不等，因此，采用式(5)直接拟合，难以对拟合过程进行控制，同时由于拟合参数处于分母位置，每次迭代运算，均会引入截断误差。得到的结果稳定性较差。所以，将式(5)可写为：

其中，c1～c3和d1～d3为与rc单元参数相关的常数。

其中，步骤s231中将脉冲放电结束瞬间后的电压特性方程确定为

其中，ts是脉冲放电后静置的时间，c1～c3和d1～d3为与rc单元参数相关的常数。

hppc实验包括先对电池进行脉冲放电，再静置。ts的计时起点为脉冲结束时，即脉冲放电结束后的时间。

其中，步骤s232为：

根据温度t下，电池在不同soc下的hppc实验脉冲放电后静置的电压响应曲线，采用(6)式通过非线性拟合得到不同soc下的c1～c3和d1～d3值。所述soc值为0.1～0.9范围内的至少9个数值，再根据下式计算得到不同soc下的rc单元参数值：

根据得到的不同soc下的ri和ci值，对r1-soc，r2-soc，r3-soc，c1-soc，c2-soc和c3-soc的参数表进行三次样条插值，得到加密后的r1-soc，r2-soc，r3-soc，c1-soc，c2-soc和c3-soc的参数表。

其中，所述步骤s233具体为，改变温度t，重复s232，获取其它温度下加密后的r1-soc，r2-soc，r3-soc，c1-soc，c2-soc和c3-soc的参数表，建立r1、r2、r3、c1、c2和c3随soc和温度的二维参数网络

进一步地，步骤s32中在计算当前温度t和时间t下的soc值时不直接采用数学软件的非线性方程求解工具求解等效电路模型得到的高度非线性方程，而采用编写程序的方式求解，包括：

i)设定soc初始值为0.9，计算电池的端电压值u；

ii)计算当前t下的电池端电压值u*与u的相对偏差

δ＝|u-u*|/u；

iii)若δ≥0.001,则令soc值减小0.001，重复i)～ii)；若δ<0.001,则输出此soc值，即为当前温度t和时间t下的soc值。

由于已经得到了式(2)uocv、r0、r1、r2、r3、c1、c2和c3在不同soc及温度t下的值，因此，步骤s31为：

等效电路端电压的表达式写为：

对于当前温度t和时间t，则式(8)中的u(t)，u1(0)、u2(0)和u3(0)和i均为已知量，且uocv、r0、r1、r2、r3、c1、c2和c3只与soc相关，则式(8)可写作

对式(9)进行求解，即可得到当前温度t和时间t下的soc值。

本发明的有益效果在于：

本发明提供一种锂离子电池的soc估计方法。该方法的原理简单，估计精度高。具体包括：

1、本发明提供的soc估计方法对锂离子电池的soc估计精度最大偏差不超过1％。

2、本发明提供的soc估计方法在对等效电路模型的rc单元参数进行非线性拟合时，改变了拟合的参数形式，能够有效提高拟合的稳定性和速度。

3、本发明提供的soc估计方法在获取等效电路模型的rc单元参数与soc的关系时，不采用多项式拟合方法，而采用三次样条插值技术建立参数表，能够有效避免多项式拟合带来的偏差。

4、本发明提供soc估计方法在求解等效电路电压特性方程时，不直接求解非线性方程，采用编写程序的方法求解，有效提高求解精度，降低求解时间。

附图说明

图1为本发明基于等效电路的电池soc的估计方法的流程图；

图2为等效电路的电路结构；

图3采用编写程序的方式求解式(9)的流程图。

图4为拟合得到的开路电压与soc的关系。

图5为拟合得到的欧姆内阻与soc的关系。

图6至图11分别为r1-soc，r2-soc，r3-soc，c1-soc，c2-soc和c3-soc的参数表。

图12为所得到的soc估计值与实验值对比，

图13估算结果的偏差情况。

具体实施方式

下面通过最佳实施例来说明本发明。本领域技术人员所应知的是，实施例只用来说明本发明而不是用来限制本发明的范围。

实施例中，如无特别说明，所用手段均为本领域常规的手段。

实施例1

本实施例结合一款正极材料为三元材料的电池，t＝25℃为例，采用以下估计方法，对其soc进行估计。

具体过程包括下列步骤：

s1、获取所述开路电压uocv与所述soc及温度t的关系

根据温度25℃下恒流放电得到的电池在不同soc下的开路电压uocv，所述soc值为0.1～0.9范围内的至少9个数值。对25℃下的uocv-soc曲线进行多项式拟拟合。

所述多项式拟合公式为：

uocv＝a0+a1soc+a2soc²+a3soc³+a4soc⁴+a5soc⁵

其中uocv表示电池开路电压，a0～a5为多项式系数，且为常数，soc为电池的荷电状态。

图4为拟合的结果，得到的开路电压与soc的关系为：

uocv＝3.3233+0.02455soc-8.9131×10^-4soc²

+1.6196×10^-5soc³-1.2246×10^-7soc⁴+3.3391×10^-10soc⁵

s2、建立等效电路模型，获取所述模型参数与所述soc及温度t的关系，该步骤包括如下子步骤：

s21、建立三阶等效电路模型，明确所述电池端电压u与开路电压uocv的特性关系。

针对图2所示电路图，建立电池模型的特性方程：

u0＝ir0

u＝uocv-u0-u1-u2-u3

其中，u0为所述欧姆内阻r0两端的电压，u1～u3为三个rc单元两端的电压，i为电流。

求解式(1)，可得端电压的表达式为：

其中，u1(0)、u2(0)和u3(0)分别为计时开始时，三个rc单元两端的电压初值。

s22、获取所述等效电路模型中的欧姆内阻r0与soc及温度t的关系。

s221、确定脉冲放电结束瞬间的电压特性。

脉冲放电结束瞬间，电流为零，图2所示电路结构为零输入响应，其电压特性方程为：

根据图2的结构可知，脉冲放电结束瞬间，电压的变化完全是由欧姆内阻r0产生。因此，欧姆内阻r0采用下式获取：

其中，ul为脉冲放电结束的电压突变，i为脉冲放电电流值。

s222、获取某相同温度下欧姆内阻r0与soc的关系

根据温度25℃下，电池在不同soc下的hppc实验得到的电压响应曲线，采用s221所述方法计算得到不同soc下的欧姆内阻r0和r0-soc曲线。所述soc值为0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8和0.9。对25℃下的r0-soc曲线进行如下的多项式拟合：

r0＝b0+b1soc+b2soc²+b3soc³+b4soc⁴+b5soc⁵

其中r0表示欧姆内阻，b0～b5为多项式系数，且为常数，soc为电池的荷电状态。

图5为拟合结果，得到的欧姆内阻与soc的关系为：

r0＝2.5800-0.03058soc-4.5770×10^-4soc²

+1.6125×10^-6soc³-8.6662×10^-8soc⁴+5.0321×10^-10soc⁵

s23、获取所述等效电路模型中的并联rc单元参数r1，c1，r2，c2，r3，c3与soc及温度t的关系。包含如下子步骤：

s231、确定脉冲放电结束瞬间后的电压特性。

由图2的电路结构可知，脉冲放电结束瞬间后，欧姆内阻两端的电压变为零，但三个rc单元两端的电压不会变为零。因此式(3)变为：

原则上，采用数学软件的非线性拟合工具，可以直接根据式(4)对电压响应曲线拟合，得到三个rc单元的参数值。但是，由于式(4)中存在指数函数，且图2结构中的电容的数值从几十到几百kf不等，同时由于拟合参数处于分母位置，每次迭代运算，均会引入截断误差。因此，采用式(5)直接拟合，难以对拟合过程进行控制，得到的结果稳定性较差。所以，将式(5)写为：

其中，c1～c3和d1～d3为与rc单元参数相关的常数。

s232、获取某相同温度下并联rc单元参数r1，c1，r2，c2，r3，c3与soc的关系。

根据温度25℃下，电池在不同soc下的hppc实验冲放电后静置的电压响应曲线，基于式(6)通过非线性拟合得到不同soc下的c1～c3和d1～d3值。

所述soc值为0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8和0.9。再根据下式计算得到不同soc下的rc单元参数值。所述表达式为：

根据步骤上述得到的不同soc下的r1～r3和c1～c3值，对r1-soc，r2-soc，r3-soc，c1-soc，c2-soc和c3-soc的参数表进行三次样条插值，得到加密后的r1-soc，r2-soc，r3-soc，c1-soc，c2-soc和c3-soc的参数表。

参数的结果见图6～11。

s3、估计当前温度t和时间t下的soc值

该步骤包含如下子步骤：

s31、简化电压特性方程

由于已经得到了式(2)uocv、r0、r1、r2、r3、c1、c2和c3在不同soc及温度t下的值，因此，式(2)可改写为：

对于当前温度t和时间t，则式(8)中的u(t)，u1(0)、u2(0)和u3(0)和i均为已知量，且uocv、r0、r1、r2、r3、c1、c2和c3只与soc相关，则式(8)可写作

对式(9)进行求解，即可得到当前温度t和电池运行的时间t下的soc值。

s32、对电压特性方程进行求解

式(9)是一个高度非线性方程，直接采用数学软件的非线性方程求解工具进行求解，无法得到稳定的求解结果，且求解时间较长。考虑到soc值本身具有上下限，因此采用编写程序的方式求解式(9)，具体的流程如图3所示。

i)设定soc初始值为0.9，根据式(9)计算电池的端电压值u；

ii)当前t下的电池端电压值u*与u的相对偏差

δ＝|u-u*|/u；

iii)若δ≥0.001。则令soc值减小0.001，重复i)～ii)。若δ<0.001,则输出此soc值，即为当前温度t和时间t下的soc值。

具体编程示例如下(只列出了求解非线性方程的程序，未列出式中各参数与soc的关系的程序)：

本实施例详细描述了本方法从参数获取到soc估计的全过程。在实际应用中，对于相同的电池，所有参数获取过程即s1和s2以及估计过程的表达式简化过程s31均只需要执行一次，获取相应的参数值。进行soc估计时只需要具体执行s32步骤。

实施效果：

所得到的soc估计值与实验值对比见图12，从图中看实验测试(experiment)和预测结果(prediction)基本完全重合，偏差情况见图13。正负的最大偏差均约为0.6％。

实施例2

采用和实施例1系统的方法，设定其他值的温度，t在低于10℃时每5℃获取一组uocv与soc的关系，t在10℃以上时每10℃获取一组uocv与soc的关系。

所得到的soc估计值与实验值对比，其最大偏差不超过1％。

以上的实施例仅仅是对本发明的优选实施方式进行描述，并非对本发明的范围进行限定，在不脱离本发明设计精神的前提下，本领域普通工程技术人员对本发明的技术方案做出的各种变型和改进，均应落入本发明的权利要求书确定的保护范围内。