一种基于蠕变延性的高温蠕变寿命预测方法与流程

本发明涉及高温构件蠕变寿命技术领域，特别是涉及一种基于蠕变延性的高温蠕变寿命预测方法，考虑蠕变延性随蠕变应变速率的变化，实现金属材料长时蠕变寿命的预测。

背景技术：

应用在火力发电站等大型设备中的高温构件，在高压高温等环境中，长时间承受各种应力的作用下，易于发生蠕变断裂，造成构件的失效，从而危及大型设备的正常安全使用，因此，精准预测蠕变寿命对高温构件的使用和设计具有非常重要的意义。寿命预测主要是以传统持久强度试验外推为主的方法，通过提高服役温度或加载应力的方法达到缩短实验时间的目的。蠕变寿命评估研究方法经过长期的发展已逐渐成熟大体经历了不同的阶段。最早是等温线外推法，但大量的实验结果表明在恒定的温度，双对数坐标下，时间和应力之间呈直线关系。在部分耐热钢的数据中是符合这一关系，但实际中有相当部分的耐热钢的持久性能试验点并不符合线性关系，低应力、长时间数据经常偏离原有的直线关系，相关研究也表明等温线外推法在评估新型耐热钢或不锈钢的持久性能时有高估的情况。为综合考虑温度和应力与蠕变持久断裂时间三者之间的关系，工程上将断裂时间和试验温度表示为时间-温度互补的参数，并和应力相关联。此方法简称ttp参数法，国内研究运用最多的是l-m参数法，虽然被广泛应用，但对其模型基础及预测精度一直存在争议，由于该方法比较难以描述蠕变机制变化引起的寿命变化。蠕变机制的变化与蠕变激活能有关，即蠕变激活能随持久时间而变化，提出分区处理的拟合方法，可以提高长时低应力下预测机制变化引起的寿命变化。随着寿命预测技术的发展，国内外开始以基于蠕变曲线的蠕变数据来进行寿命外推，利用短时的蠕变数据通过精确的模型预测长时的蠕变曲线从而进行精确的寿命预测，运用最多的是θ投影法，在不同断裂模式下，均可运用θ投影法处理蠕变性能数据，其优点是可以不考虑断裂模式的变化对持久寿命外推的影响，但更适用于短时蠕变寿命的预测。

近几年，从自然界事物普遍适用的热力学基本定律推导而出的蠕变断裂寿命计算方法越来越受到研究学者们的重视，此类模型具有材料参数拟合方法简单，而且一般具有较高的预测精度，是高温构件损伤评估和寿命预测的一个新的方向。

技术实现要素：

本发明的目的是为应用在高温高压环境中的大型重要设备上的高温承压构件的蠕变断裂寿命预测提供一种新的计算方法；基于蠕变延性并考虑蠕变延性与蠕变应变速率相关性，提出的一种新的金属材料高温蠕变寿命的计算方法。

为实现本发明的目的所采用的技术方案是：

一种基于蠕变延性的高温蠕变寿命计算方法，包括以下步骤：

步骤1，获取高温条件下材料不同应力水平的蠕变性能的数据，每个试验点包括材料的应力σ(单位为mpa)、断裂时间tf(单位为h)、最小蠕变应变速率(单位为h^-1)、蠕变延性εf(单位为％)、最大蠕变断裂应变εmax(单位为％)和最小蠕变断裂应变εmin(单位为％)；

步骤2，将步骤1中试验数据按照式利用数学分析软件(可采用matlab，origin等软件)，按最小二乘法回归，求出待定系数b和n；

步骤3，将步骤1中的试验数据按照式利用数学分析软件(可采用matlab，origin等软件)，按最小二乘法回归，将不同应力水平下的最小蠕变应变速率蠕变延性εf、最大蠕变断裂应变εmax、最小蠕变断裂应变εmin输入计算机，运行数学分析软件(可采用matlab，origin等软件)，求得待定系数α和

步骤4，根据能量守恒定律和熵守恒定律的蠕变断裂时间与应力和蠕变延性的关系式利用步骤1中的tf和σ、εf的值，采用非线性数值拟合方法(可采用matlab，origin等软件)求得系数k和p；

步骤5，利用寿命预测模型预测材料的高温蠕变寿命，所述寿命预测模型中的b和n由步骤2得到，所述寿命预测模型中的α和由步骤3得到，所述寿命预测模型中的k和p由步骤4得到。

在上述技术方案中，所述高温蠕变寿命计算方法适用应力水平为0.2σys-σys，其中σys为材料屈服强度。

在上述技术方案中，所述高温蠕变寿命计算方法适用作业温度为400-1200℃。

与现有技术相比，本发明的有益效果是：

1.本发明提出的寿命预测方法考虑蠕变延性与最小蠕变速率的相关性，克服了由于蠕变应变变化引起的最小蠕变速率快速衰减导致的无法实现金属材料长期寿命的准确预测的难题。

2.提高了材料蠕变寿命预测的精度，适用于各种高温金属材料。

3.预测方法简单，所需要的数据采用常规的材料蠕变性能的测试获得。

附图说明

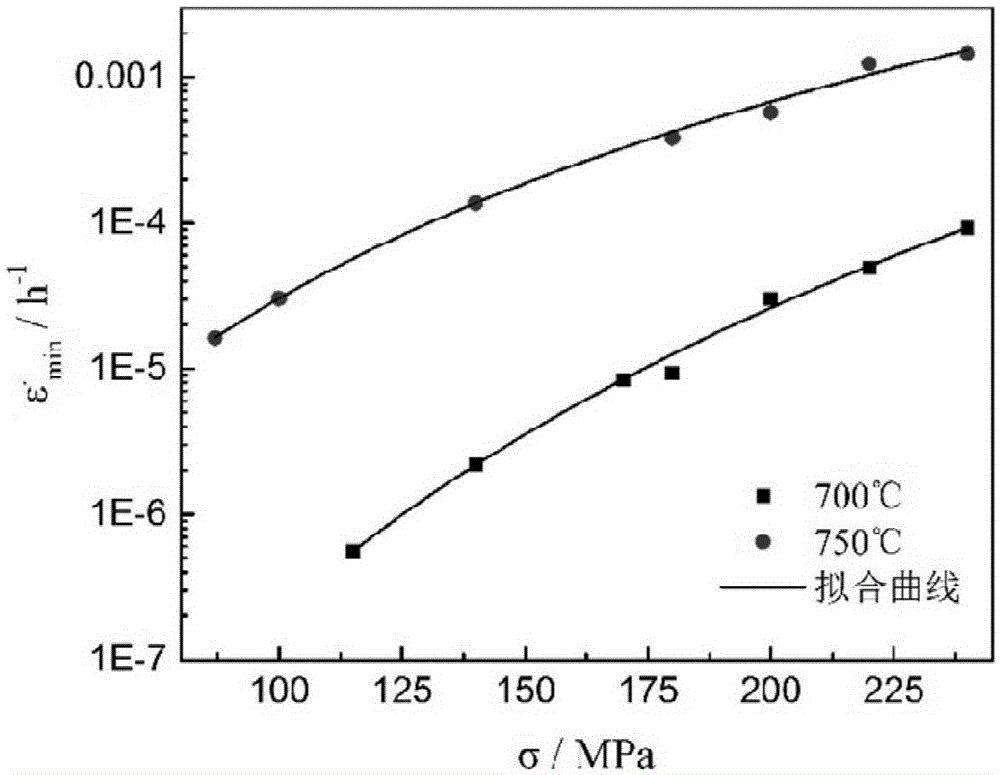
图1是参数b和n值的拟合曲线图。

图2是蠕变延性与最小蠕变应变速率的拟合曲线，用以确定公式中和α的值。

图3是参数k和p值的拟合曲线图。

图4是基于蠕变延性的高温蠕变寿命预测方法的寿命预测曲线与试验值的比较。

具体实施方式

采用本发明提供的一种更加精确地基于蠕变延性的高温蠕变寿命预测方法，对sanicro25钢在700℃和750℃不同应力水平下进行蠕变寿命预测分析。

第一步：获取材料不同温度、不同应力水平下蠕变性能的数据。

试验按照gb/t2039-2012《金属拉伸蠕变持久试验方法》进行。试样尺寸：直径为5mm的标准圆棒试样，标距为50mm。试验设备为高温蠕变持久强度试验机。该试验机的组成如下：主机；加热炉；温度测控系统；变形测量系统。其负荷范围为0.3-30kn，载荷误差小于等于±1％。蠕变自动记录仪的量程为：0-10mm，测量误差不超过±0.1％。首先将试样安装在试验机上，安装好引伸计，检查试样的同轴度在规定的范围内，若超出应当按要求调整。试样安装好之后，先施加预载荷200n，并开始升温加热到预定温度然后保持60min。最后施加总载荷，记录断裂时间。在此试验中，试验温度为700℃和750℃，应力水平为:87-240mpa。试验结束，整理得到不同温度和应力水平下材料的蠕变性能数据，包括：材料的应力σ(单位为mpa)、断裂时间tf(单位为h)、最小蠕变应变速率(单位为h^-1)，蠕变延性εf(单位为％)、最大蠕变断裂应变εmax(单位为％)和最小蠕变断裂应变εmin(单位为％)。

第二步：采用诺顿函数来表示最小蠕变应变速率与应力σ的关系。由表1中蠕变试验数据中的与σ的值，按照式利用数学分析软件(可采用matlab，origin等软件)，按最小二乘法回归，求出待定系数b和n。b和n参数的拟合曲线如图2所示，b和n的值列于表2。

表1不同温度和应力水平下材料的σ、和εf数据

表2700℃和750℃条件下分析出的b和n参数的值

第三步：按照式利用数学分析软件(可采用matlab，origin等软件)，按最小二乘法回归可得到α的值。具体可将实验数据(如表1所示)中得到的最小蠕变应变速率与蠕变延性值的对应关系做成散点图(其中εmax对应εf的最大值，εmin对应εf的最小值)，对数据点在数学分析软件中进行非线性拟合，得到sanicro25钢的蠕变延性与最小蠕变应变速率的拟合曲线，如图3所示，并可获得参数α和的值，结果如表3所示。

表3700℃和750℃条件下分析出的参数α和的值

第四步：基于蠕变断裂时间与应力和破断蠕变量的关系式利用试验数据，采用非线性数值拟合方法(可采用matlab，origin等软件)求系数k和p。根据蠕变试验数据中的tf和σ、εf的值(见表4)，拟合得到如图3所示的曲线，由此可以获得参数k与p的值，其结果列于表5。至此可以得到金属材料高温寿命预测所需的所有参数。

表4不同温度和应力水平下材料的σ、εf、tf和数据

表5700℃和750℃条件下分析出的参数α和的值

第五步：本发明提出的考虑蠕变延性的金属材料高温蠕变寿命预测方法如式1所示：

式1中所需参数可由步骤1和步骤4获得。

将步骤1和步骤4获得参数代入公式(1)，则得到sanicro25钢不同温度下基于蠕变延性的高温蠕变寿命预测模型。

即在700℃下：

在750℃下：

图4是利用本发明提出的蠕变寿命预测方法对sanicro25钢的高温蠕变寿命预测结果，图中散点是文献(chaig,hernblomj,peltolat,etal.creepbehaviorinanewlydevelopedheatresistantausteniticstainlesssteel[j].bhmberg-undmonatshefte,2015,160(9):400-405.)报道的蠕变寿命数值，曲线是利用本发明的预测方法模拟出的曲线。和实际的sanicro25钢高温蠕变寿命对比，实现了低应力下蠕变寿命快速衰减趋势准确模拟。可以发现本发明的基于蠕变延性的高温蠕变寿命方法，能够简便并且较高精度地计算得到蠕变寿命。

以上所述仅是本发明的优选实施方式，应当指出的是，对于本技术领域的普通技术人员来说，在不脱离本发明原理的前提下，还可以做出若干改进和润饰，这些改进和润饰也应视为本发明的保护范围。