一种基于分维数的土颗粒级配评价方法与流程

本发明属于岩土工程中颗粒分布微观分形及土体物理性质研究技术领域，具体涉及一种基于分维数的土颗粒级配评价方法。

背景技术：

定量评价土体颗粒级配，反映土体的物理性质，是岩土介质工程性质研究的基础。颗粒级配对无粘性土的渗透变形、砂土变形、土体不排水力学特性、粗粒土渗透系数、动载下的压实性能都有着很大的影响。在软弱土加固处理、土石方填筑施工、路基工后沉降的分析预测、边坡坡体降水等工程应用方面占有举足轻重的地位。

分形理论在岩土工程中应用广泛。在分维数的应用方面，目前为止多集中在岩土体孔隙率、水分特征曲线、渗透性、土体强度方面，而且孔隙体积-孔径分布分维数、颗粒(孔隙)原状面积分布分维数在研究岩土体原状特性时的潜力比较明显。

岩土介质的微观、细观结构决定其宏观特性，将其微观、细观的定量化指标与宏观物理力学特性联系起来，有望从新的角度去解释岩土工程中的复杂现象。岩土体微观、细观孔隙和颗粒的大小和形状相异，表现出“无序”的特征。大量研究表明，它们表现出分形特性，因而分形理论成为岩土介质微观、细观特性研究的有效手段。

因此建立颗粒分布微观分形特性(土体颗粒分维数d)与不均匀系数(cu)、曲率系数(cc)的关系，简化土体颗粒级配评价方法，在路堤、堤坝填土的工程应用、岩土介质细观特性与宏观物理力学性质的研究等方面具有极其重要的意义。

对于土颗粒级配的评价方法，目前一般是通过进行颗粒筛分试验确定土体的特征粒径以计算不均匀系数(cu)和曲率系数(cc)，结合土颗粒级配评价标准从而评价土颗粒级配。这种方法相对繁琐，不够直观有效地判断土体的级配好坏。

技术实现要素：

本发明的目的就是针对上述技术的不足，提供一种简化、直观的基于分维数的土颗粒级配评价方法。

为实现上述目的，本发明所设计的基于分维数的土颗粒级配评价方法，包括如下步骤：

1)以谢尔宾斯基地毯(sierpinski地毯)分形模型和门格海绵(menger海绵)为基础，提出土体小于某粒径的含量与土体颗粒分维数之间的关系

m是粒径区间0～r的颗粒总质量、mt为土体样本的总质量、r为颗粒粒径、rmax为最大粒径；

2)计算土体颗粒分维数d及推导di

将ⅰ式变形可得土体颗粒分维数d的计算公式：

其中km＝m/mt为小于某粒径的颗粒质量所占比例、kr＝r/rmax为某粒径与最大粒径之比、d为土体颗粒分维数；

令m/mt＝i％，带入ⅰ式为：

变形得：

di为小于某粒径的土粒质量占总质量i％的粒径，rmax为最大粒径，其中i取值为10、20、30、40、50、60、70、80、90或100；

3)结合土体不均匀系数cu和土体曲率系数cc，以及结合《土的工程分类标准》，用土体颗粒分维数d评价土体颗粒级配

用土体颗粒分维数d评价土体颗粒级配的标准如下：

对于级配连续的土：若公式ⅱ中计算的土体颗粒分维数d＞1.89，级配良好，若公式ⅱ中计算的土体颗粒分维数d＜1.89，级配不良；

对于级配不连续的土：若公式ⅱ中计算的土体颗粒分维数1.89＜d＜2.63，级配良好，反之则级配不良。

进一步地，所述步骤1)的具体推导过程如下：

以谢尔宾斯基地毯(sierpinski地毯)分形模型和门格海绵(menger海绵)分形模型为基础，推导出颗粒粒径分布密度函数，即：

f(r)＝cr^-1-dⅳ

式中：r为颗粒粒径；c为常数；d为土体颗粒分维数，0＜d＜3；

假设颗粒的体积形状因子kv为恒定值，颗粒密度用ρ表示，则某粒径区间r1～r2(r1＜r2)上的颗粒质量可表示为

式中：c^*＝ρkvc/(3-d)

假设土体样本的总质量为mt，最大粒径是rmax，最小粒径是0，则可令r1＝0，r2＝rmax，根据ⅴ式有mt＝c^*rmax^3-d，故c^*＝mt/rmax^3-d带入ⅴ式有：

若最小粒径为0，则m可认为是粒径区间0～r的颗粒总质量，由ⅵ式可得：

进一步地，所述步骤3)的具体过程如下：

将公式ⅲ带入土体不均匀系数定义和土体曲率系数定义中得出

土体不均匀系数为：

土体曲率系数为：

结合《土的工程分类标准》

对于级配连续的土：cu＞5计算得出d＞1.89，级配良好；cu＜5即d＜1.89，级配不良；

对于级配不连续的土：需同时满足cu＞5和1＜cc＜3计算得出1.89＜d＜2.63，级配良好；反之则级配不良；

用土体颗粒分维数d评价土体颗粒级配的标准如下：

对于级配连续的土：若公式ⅱ中计算的土体颗粒分维数d＞1.89，级配良好，若公式ⅱ中计算的土体颗粒分维数d＜1.89，级配不良；

对于级配不连续的土：若公式ⅱ中计算的土体颗粒分维数1.89＜d＜2.63，级配良好，反之则级配不良。

与现有技术相比，本发明具有以下优点：本发明建立了颗粒分布微观分形特性(土体颗粒分维数d)与不均匀系数(cu)、曲率系数(cc)的关系，简化了土体颗粒级配评价方法，能够直观有效地判断土体的级配好坏，在路堤、堤坝填土的工程应用、岩土介质细观特性与宏观物理力学性质的研究等方面具有极其重要的价值。

附图说明

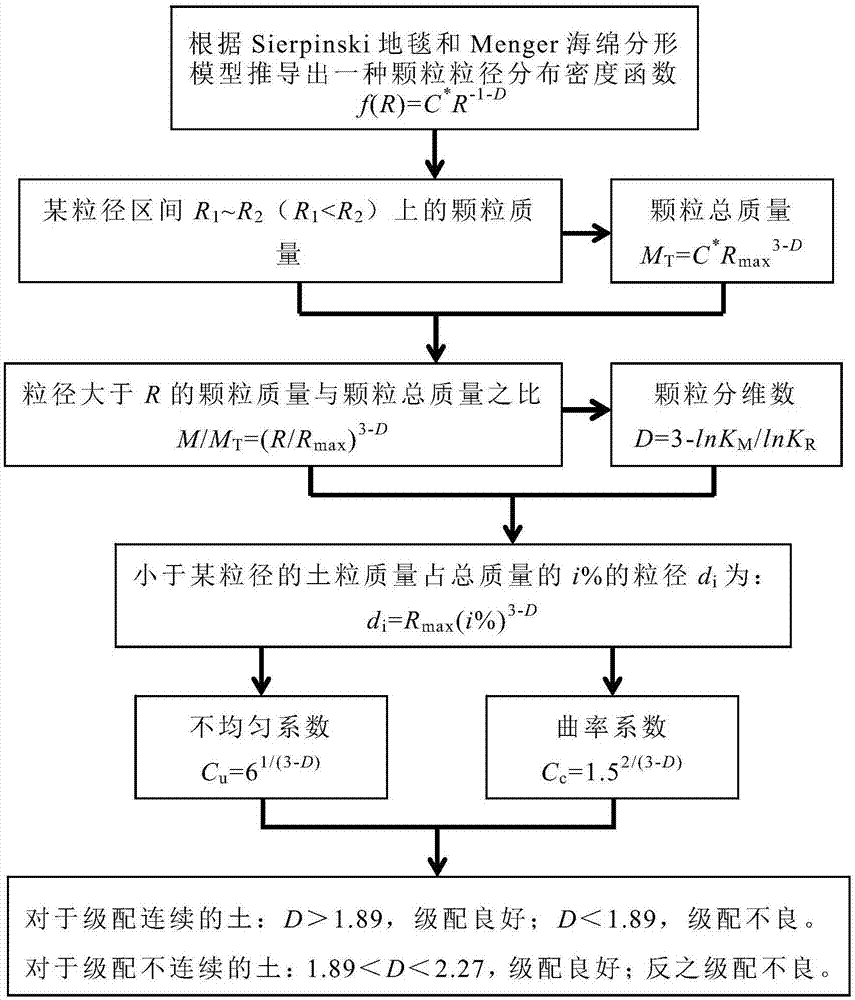
图1为本发明基于分维数的土颗粒级配评价方法流程示意图；

图2为土体颗粒分维数d和不均匀系数cu的关系；

图3为土体颗粒分维数d和不均匀系数cu及曲率系数cc的关系；

图4为国内不同地区土样不均匀系数cu与土体颗粒分维数d关系的实测与预测的对比图。

具体实施方式

下面结合附图和具体实施例对本发明作进一步的详细说明。

如图1所示基于分维数的土颗粒级配评价方法，包括如下步骤：

1)提出土体小于某粒径的含量与土体颗粒分维数之间的关系

以谢尔宾斯基地毯(sierpinski地毯)分形模型和门格海绵(menger海绵)分形模型为基础，推导出颗粒粒径分布密度函数，即：

f(r)＝cr^-1-dⅳ

式中：r为颗粒粒径；c为常数；d为土体颗粒分维数，0＜d＜3；

假设颗粒的体积形状因子kv为恒定值，颗粒密度用ρ表示，则某粒径区间r1～r2(r1＜r2)上的颗粒质量可表示为

式中：c^*＝ρkvc/(3-d)

假设土体样本的总质量为mt，最大粒径是rmax，最小粒径是0，则可令r1＝0，r2＝rmax，根据ⅴ式有mt＝c^*rmax^3-d，故c^*＝mt/rmax^3-d带入ⅴ式有：

若最小粒径为0，则m可认为是粒径区间0～r的颗粒总质量，由ⅵ式可得：

2)计算土体颗粒分维数d及推导di

将ⅰ式变形可得土体颗粒分维数d的计算公式：

其中km＝m/mt为小于某粒径的颗粒质量所占比例、kr＝r/rmax为某粒径与最大粒径之比、d为土体颗粒分维数；

令m/mt＝i％，带入ⅰ式为：

变形得：

di为小于某粒径的土粒质量占总质量i％的粒径，rmax为最大粒径，其中i取值为10、20、30、40、50、60、70、80、90或100；

3)结合土体不均匀系数cu和土体曲率系数cc，以及结合《土的工程分类标准》(gbt50145-2007)，用土体颗粒分维数d评价土体颗粒级配

将公式ⅲ带入土体不均匀系数定义和土体曲率系数定义中得出

土体不均匀系数为：

土体曲率系数为：

结合《土的工程分类标准》

对于级配连续的土：如图2所示，cu＞5计算得出d＞1.89，级配良好；cu＜5即d＜1.89，级配不良；

对于级配不连续的土：如图3所示，需同时满足cu＞5和1＜cc＜3计算得出1.89＜d＜2.63，级配良好；反之则级配不良；

用土体颗粒分维数d评价土体颗粒级配的标准如下：

对于级配连续的土：若公式ⅱ中计算的土体颗粒分维数d＞1.89，级配良好，若公式ⅱ中计算的土体颗粒分维数d＜1.89，级配不良；

对于级配不连续的土：若公式ⅱ中计算的土体颗粒分维数1.89＜d＜2.63，级配良好，反之则级配不良。

下面结合具体例子本发明做进一步阐述

实施例所用的数据来源为：文献《土体渗透变形及渗透破坏过程中分形特征初探》土样数据。

对国内不同地区质量积累连续型的10组土样做了颗粒分析试验，测得土样的分维数d’和不均匀系数cu’如表1所示，绘制了土体不均匀系数cu’与分维数d’的散点图，如图4所示。

利用实测的分维数d’，结合ⅸ式，拟合得到预测的不均匀系数cu值，预测结果如图4所示，与实测值吻合良好

表1实测分维数d’和不均匀系数cu’与预测不均匀系数cu