一种动力电池荷电状态在线估算方法及系统与流程

本发明涉及新能源汽车领域,具体涉及一种动力电池荷电状态在线评估方法及系统。

背景技术：

随着国家对新能源电动汽车、电动摩托车的大力推广，动力电池的市场需求越来越大，但同时对电池的容量、寿命和成本的要求也越来越高，其中电池寿命很大程度上取决于使用方式。为了正确合理地使用电池、避免对电池造成损害，需要足够准确地估计电池的当前电池荷电状态。动力电池荷电状态(soc)的评估及实时反应速度对整车控制具有重要意义。

传统的soc估算方法包括安时积分法、开路电压法、卡尔曼滤波法等。安时积分法是以初始电量为基准，对充放电流积分得到电量的实时变化；方法优点是简单易实现，缺点是对初值依赖和误差累积难以消除。开路电压法是根据开路电压(ocv)与soc的单调对应关系、通过测量ocv计算soc；缺点是ocv测量需要在电池未工作时且充分静置一段时间后才能进行。卡尔曼滤波法是基于系统模型对电池状态作最小均方差意义上的最优估计，方法优点是误差纠正能力强，缺点是对模型准确性依赖性较高；电池作为慢时变非线性系统，参数实时变化，模型参数不确定性较强。

另外，有些方法采用带遗忘因子的递推最小二乘法(rls)对电池时变参数动态跟踪，从而构建较准确的电池系统模型，再结合扩展卡尔曼算法对系统噪声和观测噪声进行滤波处理，减小估算误差，不失为一个较理想的解决方案。然而，传统rls方法在数据统计分析中计算量偏大，扩展卡尔曼算法使用的多为三状态方程(soc和两rc电路上电压)附加一观测方程(端路电压)的系统模型，计算过程用到过多的时变参数(如电容、电阻、内阻等)，不仅积累了rls参数辨识中误差，同时使soc计算复杂化。

综上，soc的在线估算及其实时反应速度对整车控制具有重要意义，然而现有的soc估算方法中计算量较大、计算过程较复杂，影响了目标的实现。

技术实现要素：

为解决上述问题，本发明针对目前存在的计算效率低、冗余计算多等问题，提供了一种过程简洁紧凑同时具有强抗噪声能力的动力电池荷电状态(soc)在线估算方法。

本发明解决其技术问题所采用的技术方案是：

一种动力电池荷电状态在线估算方法，所述的估算方法采用以下步骤：

步骤1：基于电压中间参数表示和协方差矩阵乔勒斯基分解的递推最小二乘法的开路电压回归计算；

步骤2：基于滞变电压模拟的开路电压纠偏；

步骤3：基于soc单变量电量状态方程的扩展卡尔曼滤波算法和简化的sage-husa自适应观测方差调整方法的soc去噪计算。

进一步地，步骤1采用以下子步骤：

步骤1a)：设置电池初始中间参数向量值θ、初始遗忘因子λ和初始协方差矩阵的乔勒斯基分解p＝udu^t，其中u是单位上三角矩阵，d是对角矩阵；

步骤1b)：读入电池当前电流电压观测向量值计算和g＝df；

步骤1c)：根据λ,f,g更新计算矩阵d和u；

步骤1d)：计算当前增益向量k和预测误差e，更新电池中间参数θ＝θ+ke；

步骤1e)：由中间参数θ反算电池原始参数，包括内阻rohm、开路电压voc，并计算开路电压的变化值dvoc；

步骤1f)：遗忘因子动态调整，当|dvoc/δt|＞δv,max，加大遗忘因子λ＝τup×λ+(1-τup)×1,τup∈[0.95,1)；否则，当|e|＞δe,max，减小遗忘因子λ＝τdownλ,τdown∈[0.98,1)；

步骤1g)：协方差动态调整，当d对角元素|dii|＜δd,min，置dii＝δd,min；当θi|＞δθ,max，置dii＝dii+δd；转步骤1b)。

更进一步地，步骤2采用以下子步骤：

步骤2a)：分别针对充电和放电过程，测量电池滞变电压衰减参数β、电流效率参数ηi、半程最大滞变电压vh,max和初始滞变电压vh,0；

步骤2b)：建立滞变电压变化数学模型

步骤2c)：用差分方法模拟计算当前滞变电压vh(tk)＝vh(tk-1)+βηii(tk-1)[vh,max-sign(i(tk-1))vh(tk-1)]×δt；

步骤2d)：开路电压纠偏处理vo＝voc(tk)-vh(tk)。

更进一步地，步骤3采用以下子步骤：

步骤3a)：建立基于soc单变量的电量状态方程soc'(t)＝ηii(t)/qn+w，其中qn＝36×ahnominal，ahnominal是电池最大电荷容量，w是系统过程噪声；

步骤3b)：根据rls算法对电池端路电压的估计v^predict(t)＝voc(t)+irohm(t)+vdl(t)+vdf(t)，得到端路电压系统观测表示：

进而建立系统观测方程左边观测值根据计算，右边vo(soc,t)由voc-soc映射表计算，v是系统测量噪声；

步骤3c)：在初始阶段，直接根据rls算法估算的开路电压和滞变电压纠偏，查表得到soc值soc＝h(vo,t),vo＝voc-vh；

步骤3d)：在后续阶段，利用扩展的卡尔曼滤波方法计算上述单状态变量系统的荷电状态值；

步骤3e)：在利用ekf算法计算soc过程中，利用带遗忘因子的简化sage-husa方法自适应地动态调整系统测量噪声v的方差，控制估算误差。

本发明还提出一种采用上述动力电池荷电状态在线估算方法的一种动力电池荷电状态在线估算系统，包括电池测量数据输入模块、电池参数更新模块、参数转换模块、中间参数更新模块、荷电状态rls-ekf循环计算模块、算法参数管理模块。

本发明的有益效果在于：

1.在基于电池二阶rc等效电路模型利用带遗忘因子的rls算法对电池时变参数进行动态跟踪时，采用了协方差矩阵乔勒斯基分解迭代计算过程，计算量小且稳定，对角矩阵元素可用于自适应调整遗忘因子；

2.针对某些类型动力电池存在开路电压与soc一对一对应关系不稳定的问题，引入对滞变电压的模拟估算，并用于对开路电压进行纠偏，保证最终开路电压对soc映射关系的准确性；

3.在利用扩展卡尔曼算法(ekf)进行soc估算时，采用仅含soc单变量电量状态方程和基于端路电压的观测方程，减免了冗余状态的更新计算和对其统计特征的假设与估算，保证了计算的实时性和响应效率。

附图说明

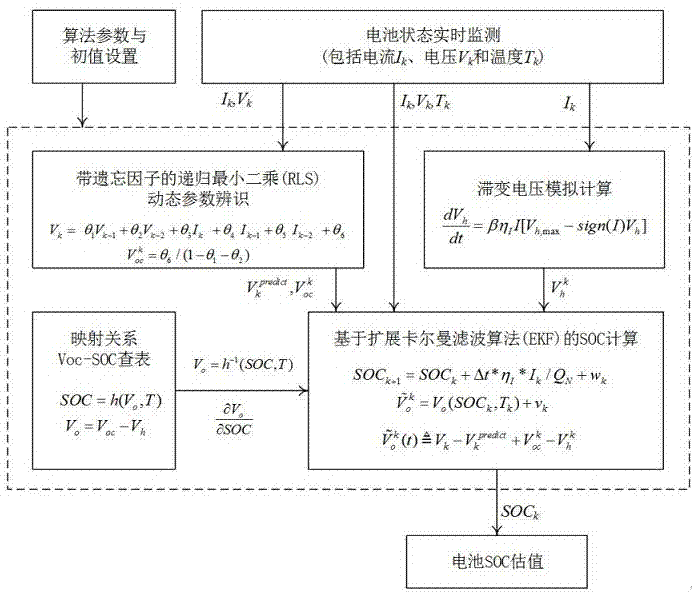
图1为本发明估算方法的估算过程图。

图2为本发明估算系统的框架结构图。

具体实施方式

为了使本发明的目的及优点更加清楚明白，以下结合实施例对本发明进行进一步详细说明。应当理解，此处所描述的具体实施例仅仅用以解释本发明，不用于限定本发明。

下面结合图1-2对该实施例进行说明。

本实施例的动力电池荷电状态在线估算方法，采用以下步骤：

步骤1：基于电压中间参数表示和协方差矩阵乔勒斯基分解的递推最小二乘法的开路电压回归计算；

步骤2：基于滞变电压模拟的开路电压纠偏；

步骤3：基于soc单变量电量状态方程的扩展卡尔曼滤波算法和简化的sage-husa自适应观测方差调整方法的soc去噪计算。

在步骤1中，取充电电流i为正号，有v＝voc+irohm+vdl+vdf，其中

v,voc,vdl,vdf,rohm分别为端路电压、开路电压、两电容电压和内阻。由二阶rc电路模型离散得到：其中vk,ik是离散的端路电压和电流，θk-1＝(θ1,θ2,...,θ6)^t是模型中间参数，是输入数据。步骤1的输出包括辨识的参数特别是开路电压和模型预测的端路电压

在步骤1的计算循环中，协方差矩阵乔勒斯基分解p＝udu^t的递推计算包含如下步骤(λ∈[0.95,1)为遗忘因子，j＝1,2,...,6)：

在步骤2中，当ik-1＞0时，取ηi＝0.99,β＝2.47×10^-5(c^-1)；当ik-1≤0时，取ηi＝1.0,β＝3.70×10^-5(c^-1)。

在步骤3中，ekf包含下列主要步骤：

初始化。k＝0设置以及

soc状态预测

均方误差预测其中是预先设置的系统噪声方差；

计算增益这里

状态更新

均方差更新

基于测量噪声统计特性估计进行测量方差更新，这里使用简化的sage-husa自适应观测方差调整方法：

b为遗忘因子，取值0.95-0.99之间；

上述更新计算采用自适应的方法，即当判断出滤波异常时才更新，否则，就不更新，这样可节省计算量。滤波异常条件是满足下列不等式：

图2为采用上述在线估算方法的动力电池荷电状态在线估算系统的实施例，该系统包括电池测量数据输入模块、电池参数更新模块、参数转换模块、中间参数更新模块、荷电状态rls-ekf循环计算模块、算法参数管理模块。

本发明提供一种计算过程简洁紧凑同时具有强抗噪声能力的动力电池荷电状态(soc)在线估算方法，该方法通过实时测量电池端路电流、电压和温度等数据，利用带遗忘因子的递推最小二乘法(rls)在电池二阶rc等效电路模型基础上对其进行回归统计分析，辨识出开路电压等电池时变参数值，同时结合滞变电压计算模型进一步对开路电压进行了纠偏处理。接着在电量状态方程以及开路电压与soc映射关系基础上利用扩展卡尔曼滤波算法(ekf)计算出稳定的soc值。为了避免电池原始参数辨识计算中的复杂性，方法采用了易处理的中间参数以及相关乔勒斯基分解迭代计算过程。在soc滤波计算阶段，方法仅用到含soc单变量电量状态方程和基于端路电压的观测方程，减免了冗余状态的更新计算和对其统计特征的假设与估算。上述两种处理策略简化了整个soc计算过程，保证了计算的实时性。同时，在考虑滞变电压、动态调整rls遗忘因子和自适应更新ekf观测方差基础上，方法能有效地对噪声进行滤波，得到稳定准确的soc曲线。在开路电压回归计算和利用实测的soc映射表的基础上，方法对soc初值误差有较强的鲁棒性。

以上所述仅是本发明的优选实施方式，应当指出，对于本技术领域的普通技术人员来说，在不脱离本发明原理的前提下，还可以作出若干改进和润饰，这些改进和润饰也应视为本发明的保护范围。