基于角度重采样与ROC-SVM的旋转机械故障诊断方法与流程

本发明属于机械设备故障诊断领域，更具体地，涉及一种对转速波动信号的角度重采样技术和基于roc-svm的旋转机械故障诊断方法及设备。
背景技术：
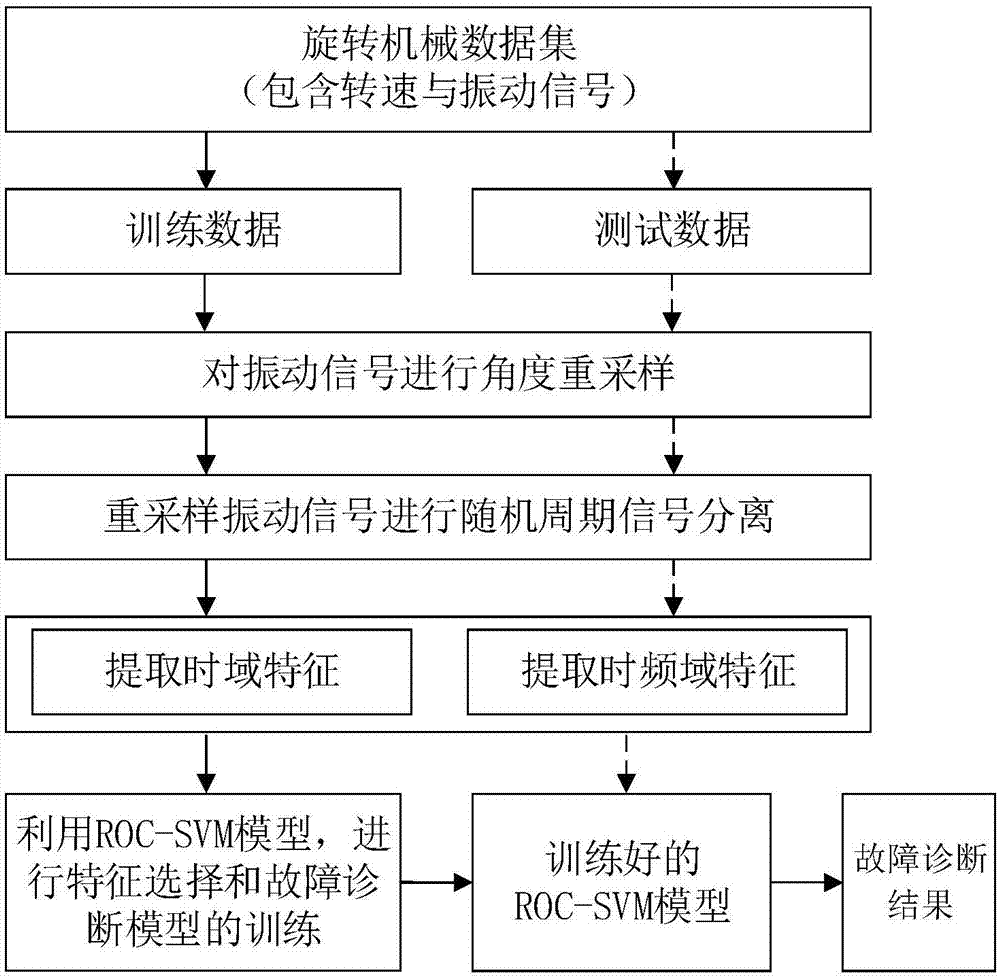
：目前，旋转机械已经成为工业设备系统中的重要组成部分，其运行状态直接影响整个系统的稳定运行。旋转机械故障会降低系统的可靠性和减少系统的使用寿命，甚至造成严重的人员伤亡与经济损失。因此，对旋转机械进行故障诊断是十分必要的。传统的旋转机械故障诊断方法大多数是基于时域分析或频域分析亦或时频域分析，但是旋转机械因转速波动而导致振动信号在等间隔内采样点并不同，并且单一的进行时域、频域、时频域分析都不能最好的得到准确评估。此外，支持向量机(supportvectormachine,svm)可以实现对损坏与非损坏的特征值分类，但是对于分类器而言最影响分类效果的还是输入特征值矩阵的大小与品质，很多基于svm的分类方法都没有好的特征提取方法。技术实现要素：针对现有技术的以上缺陷或改进需求，本发明提供了一种基于角度重采样与roc-svm的旋转机械故障诊断方法，其目的在于，通过角度重采样技术消除转速波动，并从时域和时频域维度进行特征值提取后，运用roc-svm实现旋转机械的特征选择与故障诊断，从而实现高精度的自动故障诊断。为实现上述目的，按照本发明的一个方面，提供了一种基于角度重采样与roc-svm的旋转机械故障诊断方法，包括如下步骤：步骤1：采集正常状态和故障模式状态下旋转机械的振动信号与转速信号，得到包含正常状态和故障状态的振动信号与转速信号的样本点；随机选取部分样本点组建训练数据集，剩余的样本点组建测试数据集；步骤2：使用同步采样的转速信号，对训练数据集中样本点的振动信号进行角度重采样，以消除转速波动引起的振动信号误差；步骤3：对步骤2重采样后的振动信号进行随机周期信号分离；步骤4：从步骤3的每个信号分离结果中提取时域特征，得到时域特征数据集；步骤5：使用小波包变换方法对步骤2重采样后的振动信号进行分解，得到分解后的模态分量，计算各模态分量的能量值作为时频域特征，得到时频域特征数据集；步骤6：将步骤4、5提取的时域特征数据集和时频域特征数据集输入roc-svm故障诊断模型中，自动选择最优特征并进行故障诊断模型的训练；步骤7：测试数据集中的样本点经步骤2至步骤5处理后，将提取的特征输入到经步骤6训练好的roc-svm故障诊断模型中进行诊断，得到诊断结果，即是否故障、若故障则属于哪种故障模式。进一步地，步骤4的时域特征包括：均值、绝对均值、最小值、方差、峰值、峰峰值、有效值、方根幅值、峭度、歪度、峭度指标、歪度指标、裕度因子、峰值指标、脉冲指标、波形指标；进一步地，步骤2的重采样过程包括如下子步骤：步骤2.1：已知振动信号的原始采样频率fs0及各个时间间隔内旋转机械的转速rpm。步骤2.2：依据原始采样频率fs0确定所需要的每转采样点数m，使得重采样之后的采样频率与原始值近似，作为需要达到的目标值；步骤2.3：计算重采样后的目标采样频率fs：fs＝m*rpm/60步骤2.4：判断当前rpm对应的时间间隔内目标采样频率fs与fs0之间的大小，如果fs大于fs0则需要利用线性插值增大此时间间隔内每秒采样点数来达到所需每转采样点数m，若fs小于fs0则需要减少此时间间隔每秒采样点数，从而保证每转采样点数m的一定；步骤2.5：按照步骤2.4调整后，最终得到使用转速信号rpm处理后的振动重采样信号；进一步地，步骤6中涉及使用roc-svm故障诊断模型对特征进行自适应选择以及故障诊断模型训练，具体实施如下描述：步骤6.1：选择所有特征中的一种；针对所选特征，将训练数据集中所有正常状态的样本的特征值组建矩阵a，所有故障状态的样本的特征值组建矩阵b；步骤6.2：将a与b中的特征值按照大小降序排序，设置一个阈值c矩阵，用于分辨故障特征值与正常状态特征值的区别；步骤6.3：构建全零矩阵fpr和tpr，长度和阈值矩阵相同；令i＝1,j＝1,w＝1；判断正常状态特征值的平均值与故障状态特征值的平均值的关系：如果故障状态特征值的平均值大于正常状态特征值的平均值，判断a(i)与c(j)，b(w)与c(j)的关系，执行循环：④若a(i)＞c(j)，则fpr(j)＝1，j＝j+1，i＝i+1；⑤若b(w)＞c(j)，则tpr(j)＝1，j＝j+1，w＝w+1；⑥若a(i)＜c(j)且b(w)＜c(j)，则j＝j+1；重复上述判断，直到j＝n+1则循环终止；如果正常状态特征值的平均值大于故障状态特征值的平均值，判断a(w)与c(j)，b(i)与c(j)的关系，执行循环：④若b(i)＞c(j)，则fpr(j)＝1，j＝j+1，i＝i+1；⑤若a(w)＞c(j)，则tpr(j)＝1，j＝j+1，w＝w+1；⑥若a(w)＜c(j)且b(i)＜c(j)，则j＝j+1；重复上述判断，直到j＝n+1则循环终止；上述循环结束后，得到用于绘制roc曲线的tpr与fpr矩阵；步骤6.4：按照如下公式对矩阵fpr和tpr进行更新：其中，p为故障状态特征值个数，n为正常状态特征值个数；更新后，得到连续从0增加到1的tpr与fpr矩阵。步骤6.5：以tpr为纵坐标，fpr为横坐标，得到roc曲线图；选取输入特征值的标准如下：①曲线必须位于从左下至右上45°延伸的直线之上，②曲线积分值越大则表示故障特征值与正常状态特征值的差异越大，则该故障特征值与正常状态特征值越益于作为roc-svm故障诊断模型的输入特征值；步骤6.6：依次选择其它的特征，重复步骤6.1至步骤6.5，得到每个特征的roc曲线，同时选择出roc曲线积分值较大的输入特征值构成特征数据集；步骤6.7：使用步骤6.6选择出的特征数据集训练roc-svm故障诊断模型。进一步地，步骤6.2中，阈值c矩阵设置为降序排序后的故障矩阵b。进一步地，步骤6.7中，利用smo参数优化的线性核函数对训练后的roc-svm故障诊断模型进行参数优化。为实现上述目的，按照本发明的另一个方面，提供了一种计算机可读存储介质，该计算机可读存储介质上存储有计算机程序，该计算机程序被处理器执行时实现如前所述的任意一种方法。为实现上述目的，按照本发明的另一个方面，提供了一种实时检测施工现场图像中多类实体对象的设备，包括如前所述的计算机可读存储介质以及处理器，处理器用于调用和处理计算机可读存储介质中存储的计算机程序。总体而言，本发明构思的以上技术方案与现有技术相比，能够取得以下有益效果：1.使用角度重采样方法能够有效的消除转速波动引起的单位时间内振动信号采样点数变化，提高了后续提取特征值的品质。2.将时域和时频域特征结合起来，达到更加广泛的特征提取，得到足够多的振动信号信息。3.使用roc-svm进行特征选择与故障诊断，选取最好的特征，防止不良特征降低故障分类器的效果。4.与现有技术比较，本发明的轴承故障诊断方法能够提高轴承故障诊断的准确性和有效性，能提高诊断速度，为解决轴承故障诊断问题提供了一种新思路。附图说明图1为本发明所述方法的流程图；图2为角度重采样的原理图；图3为采样点重采样后的振动信号图；图4为小波包变换四层分解的小波包分解树；图5为小波包变换第四层16组模态分量的时间频率图；图6的(a)～(o)为所选择特征的roc曲线图。具体实施方式为了使本发明的目的、技术方案及优点更加清楚明白，以下结合附图及实施例，对本发明进行进一步详细说明。应当理解，此处所描述的具体实施例仅仅用以解释本发明，并不用于限定本发明。此外，下面所描述的本发明各个实施方式中所涉及到的技术特征只要彼此之间未构成冲突就可以相互组合。如图1～2所示，本发明优选实施例的角度重采样与roc-svm滚动轴承故障诊断方法，包括以下步骤：步骤1：用加速度传感器与转速计传感器分别采集正常状态和故障模式状态下旋转机械的振动信号与转速信号。得到包含正常状态和故障状态的振动信号与转速信号的样本点。随机选取部分样本点组建训练数据集，剩余的样本点组建测试数据集。步骤2：使用同步采样的转速信号，对训练数据集中样本点的振动信号进行角度重采样，消除转速波动引起的振动信号误差。步骤3：对重采样后的振动信号进行随机周期信号分离。步骤4：使用重采样振动信号提取时域特征，包括：均值、绝对均值、最小值、方差、峰值、峰峰值、有效值、方根幅值、峭度、歪度、峭度指标、歪度指标、裕度因子、峰值指标、脉冲指标、波形指标。步骤5：如图4、5，使用小波包变换方法对重采样振动信号进行分解，得到分解后的模态分量，计算各模态分量的能量值作为时频域特征。步骤6：将所有提取的特征数据集输入roc-svm故障诊断模型中，自适应选择最优特征并进行故障诊断模型的训练。步骤7：测试数据集中的样本点经步骤3至步骤6处理后，将提取的特征输入到训练好的roc-svm故障诊断模型中进行诊断，得到诊断结果。其中，步骤2涉及到角度重采样技术，其实施步骤由图2解释。具体过程如下：步骤2.1：已知振动信号的采样频率fs0，由转速计得到转速rpm，fs0是传感器进行采样时的采样频率，因为此时采样频率是一定的但转速可能有波动，每转采样的点数不是固定的，所以需要进行之后的角度重采样来将转速波动消除。步骤2.2：依据原始采样频率确定所需要的每转采样点数m，使得重采样之后的采样频率与原始值近似，作为需要达到的目标值。这里m值是一个固定目标值，需要更改的是每秒采样点数，从而利用对原始采样频率fs0的改变来达到每转采样点数m的不变的目的，即角度域平均采样。步骤2.3：计算重采样后的目标采样频率fs。fs是为了保证每转采样点数一定而需要达到的目标采样频率值：fs＝m*rpm/60步骤2.4：判断采样频率fs与fs0之间大小，如果fs大于fs0则需要利用线性插值增大此时间间隔内每秒采样点数来达到所需每转采样点数m，若fs小于fs0则需要减少此时间间隔每秒采样点数，从而保证每转采样点数m的一定；步骤2.5：按照步骤2.5调整后，最终得到使用转速信号rpm处理后的振动重采样信号，如图3。步骤6中涉及使用roc-svm故障诊断模型对特征进行自适应选择以及故障诊断模型训练，具体实施步骤如下：步骤6.1：选择所有特征中的一种。针对所选特征，将训练数据集中所有正常状态的样本的特征值组建矩阵a，所有故障状态的样本的特征值组建矩阵b。步骤6.2：将a与b中的值以大小降序排序，设置阈值c矩阵来分辨故障特征值与正常状态特征值的区别，本实施例中阈值c设置为排序后的故障矩阵b。步骤6.3：构建全零矩阵fpr和tpr，长度和阈值矩阵相同。令i＝1,j＝1,w＝1。tpr与fpr矩阵用于roc曲线绘制，其保存的数据为在各个不同的固定阈值下，某一特征的故障特征值和正常状态特征值与阈值的关系，从而判断某一特征的正常状态特征值与故障状态特征值的区别度大小，从而判断此特征值是否适合用于区分正常状态与故障状态。判断正常状态特征值的平均值与故障状态特征值的平均值的关系：如果故障状态特征值的平均值大于正常状态特征值的平均值，判断a(i)与c(j)，b(w)与c(j)的关系，执行循环：⑦若a(i)＞c(j)，则fpr(j)＝1，j＝j+1，i＝i+1。⑧若b(w)＞c(j)，则tpr(j)＝1，j＝j+1，w＝w+1。⑨若a(i)＜c(j)且b(w)＜c(j)，则j＝j+1。重复上述判断，直到j＝n+1则循环终止。如果正常状态特征值的平均值大于故障状态特征值的平均值，判断a(w)与c(j)，b(i)与c(j)的关系，执行循环：。⑦若b(i)＞c(j)，则fpr(j)＝1，j＝j+1，i＝i+1。⑧若a(w)＞c(j)，则tpr(j)＝1，j＝j+1，w＝w+1。⑨若a(w)＜c(j)且b(i)＜c(j)，则j＝j+1。重复上述判断，直到j＝n+1则循环终止。上述循环的目的就是将正常状态特征值与故障状态特征值与阈值c进行比较并将逻辑关系放进tpr与fpr矩阵中，上述循环结束后，得到用于绘制roc曲线的tpr与fpr矩阵。步骤6.4：更新矩阵fpr和tpr：其中p为故障状态特征值个数，n为正常状态特征值个数。更新后，得到连续从0增加到1的tpr与fpr矩阵。tpr与fpr矩阵表示与从大到小的阈值比较后，某一特征的正常状态特征值与故障状态特征值相对于阈值的大小逻辑关系，绘制roc曲线需要得到连续从0增加到1的tpr与fpr矩阵，故需进行前面的循环来得到所需矩阵，最终绘制roc曲线是tpr与fpr分别从0增加至1的曲线，可参照附图6。步骤6.5：以tpr为纵坐标，fpr为横坐标，得到roc曲线图。曲线积分值越大则表示故障特征值与正常状态特征值的差异越大，越益于做roc-svm故障诊断模型的输入特征值。另外，若曲线为附图6中的45°虚线直线，则表示这种特征的两种状态特征值区别不大，不适合作为分类器输入，曲线应高于45°虚线直线。步骤6.6：依次选择其它的特征，重复步骤6.1至步骤6.5，得到每个特征的roc曲线，自动选择出roc曲线积分值较大的特征数据。优选地，选择曲线与x(fpr)轴围成面积最大的特征数据。在其他实施例中，根据实际工程需求可以调整所需要的特征数量，只要满足步骤6.6所述的条件都可以当做合适的特征。步骤6.7：将选择出的特征数据用于训练roc-svm故障诊断模型，利用smo参数优化的线性核函数对roc-svm故障诊断模型进行参数优化。在上述步骤中，步骤6.1～6.5是运用roc曲线理论来对提取出的多个特征进行筛选，得到最适合进行svm分类的特征。roc曲线用来将多个特征进行筛选得到适合输入进svm分类器中的特征，其目标是得到不同状态值区别最大的特征。svm是一种二分类器，用来得到一个二维的分类线或高维的分类面(广义)，从而之后输入测试集来对测试集中的点进行二分类。筛选出的特征作为训练数据集输入进svm模型中进行分类器训练，得到的是一个可以对测试集进行分类的分类器，不需要进行额外处理即可直接使用。为了证明本方法的有效性，使用美国losalamos国家实验室和美国加州大学圣地亚哥分校spectraquest机械故障模拟实验平台的滚动轴承故障监测实验数据来验证本方法。实验装置包括主轴、电机、两个球轴承、齿轮箱、皮带传动。主轴由电机驱动，传动方式为皮带传动，传动比为1:2.71。主轴上安装了两个滚珠轴承，轴承为mbmfg生产的er-12k滚子轴承。主轴上安装了转速计，轴承盖顶部安装了振动传感器。滚动轴承故障监测实验数据集中包含四种数据，分别为轴承滚子在正常状态下的转速信号数据和振动信号数据以及故障状态下的转速信号数据和振动信号数据。每一种信号数据有64组，每一组包含了10240个采样数据，采样频率为2048hz。数据共包含2种状态，即正常状态和故障状态。将正常状态的标签设置为1，故障状态的标签设置为2。为了增加样本量，对64组正常状态下的信号数据和故障状态下的信号数据进行分割，每组分割为10个子组。将每一组视为一个样本点，即此时有640组正常状态的样本点和640组故障状态的样本点。进一步，随机选取状态1的80％的样本点和状态2的80％的样本点组建训练数据集，剩余的样本点组建训练数据集。进一步，使用同步采样的转速信号，对训练数据集中样本点的振动信号进行角度重采样，消除转速波动引起的振动信号误差。重采样时每转采样数rpm＝512，得到128组重采样数据。采样点重采样后的振动信号图如图三所示。进一步，对重采样后的振动信号进行随机周期信号分离。进一步，使用重采样振动信号提取时域特征，包括：均值、绝对均值、最小值、方差、峰值、峰峰值、有效值、方根幅值、峭度、歪度、峭度指标、歪度指标、裕度因子、峰值指标、脉冲指标、波形指标。进一步，接着使用小波包变换方法对重采样振动信号进行分解，本实验选用四层分解，得到16个模态分量，计算各模态分量的能量值作为时频域特征。小波包变换四层分解的小波包分解树如图四所示。分解后第四层16个模态分量的时序频率图如图五所示。进一步，将所有特征输入到roc-svm故障诊断模型中，让roc-svm故障诊断模型依据特征的roc曲线选择出合适的特征数据作为故障诊断模型的训练数据，利用smo参数优化的线性核函数对roc-svm故障诊断模型进行参数优化。选择出的15个特征的roc曲线如图六所示。将测试数据集中的样本点经步骤3至步骤6处理后，将提取的特征输入到训练好的roc-svm故障诊断模型中进行诊断，得到诊断结果。得到的诊断结果如表1所示。表1测试数据集诊断结果为了说明本方法的准确性，将本方法与未使用角度重采样及roc特征筛选的传统故障诊断方法和基于bp神经网络的故障诊断方法进行了对比，结果显示，本方法的故障识别正确率优于其他两种方法。表2不同方法之间比较方法正确率(％)本发明的方法100％未使用角度重采样及roc特征筛选的传统故障诊断方法99.6％基于bp神经网络的故障诊断方法95％本领域的技术人员容易理解，以上所述仅为本发明的较佳实施例而已，并不用以限制本发明，凡在本发明的精神和原则之内所作的任何修改、等同替换和改进等，均应包含在本发明的保护范围之内。当前第1页12